30 câu Trắc nghiệm Làm quen với xác suất của biến cố (có đáp án 2024) – Toán 7 Kết nối tri thức
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 2: Làm quen với xác suất của biến cố đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 2.
Trắc nghiệm Toán 7 Bài 30: Làm quen với xác suất của biến cố
Câu 1. Gieo một con xúc xắc được chế tạo cân đối. Tính xác suất của biến cố “Số chấm xuất hiện trên mặt con xúc xắc là 2”.
A. 2;
B. 1;
C. 13;
D. 16.
Đáp án đúng là: D
Khi gieo một con xúc xắc thì ta có các biến cố:
A1: “Số chấm xuất hiện trên mặt con xúc xắc là 1”
A2: “Số chấm xuất hiện trên mặt con xúc xắc là 2”
A3: “Số chấm xuất hiện trên mặt con xúc xắc là 3”
A4: “Số chấm xuất hiện trên mặt con xúc xắc là 4”
A5: “Số chấm xuất hiện trên mặt con xúc xắc là 5”
A6: “Số chấm xuất hiện trên mặt con xúc xắc là 6”
Khi gieo một con xúc xắc được chế tạo cân đối thì 6 mặt của nó có khả năng xuất hiện như nhau. Do đó 6 biến cố trên đồng khả năng. Mặt khác, trong mỗi lượt gieo luôn xảy ra duy nhất một trong 6 biến cố trên nên xác suất của chúng bằng nhau và bằng 16.
Vậy xác suất của biến cố “Số chấm xuất hiện trên mặt con xúc xắc là 2” là 16.
Câu 2. Xác suất của biến cố “Ngày mai, lớp em có cô giáo mới sinh năm 1700” bằng
A. 1;
B. 0,99;
C. 0;
D. Không xác định.
Đáp án đúng là: C
Cô giáo sinh năm 1700 đến nay đã hơn 300 tuổi, do đó việc lớp em có cô giáo hơn 300 tuổi là điều biết trước không bao giờ xảy ra. Do đó biến cố “Ngày mai, lớp em có cô giáo mới sinh năm 1700” là biến cố không thể nên có xác suất bằng 0.
Câu 3. Có hai chiếc hộp, mỗi hộp đựng 5 tấm thẻ ghi các số 1; 2; 3; 4; 5. Rút ngẫu nhiên từ mỗi hộp một tấm thẻ. Biến cố “Tổng các số ghi trên hai tấm thẻ nhỏ hơn 11” có xác suất bằng
A. 1;
B. 0,5;
C. 0;
D. 0,99.
Đáp án đúng là: A
Số lớn nhất ghi trên mỗi tấm thẻ là 5 nên tổng các số ghi trên hai tấm thẻ lớn nhất là 10.
Do đó, tổng các số ghi trên hai tấm thẻ luôn nhỏ hơn 11.
Vậy biến cố “Tổng các số ghi trên hai tấm thẻ nhỏ hơn 11” là biến cố chắc chắn nên có xác suất bằng 1.
Câu 4. Lớp 7A có có 12 bạn nữ và 12 bạn nam. Giáo viên chọn ngẫu nhiên 1 bạn lên bảng kiểm tra bài cũ. Biến cố “Bạn được gọi là bạn nam” có xác suất là
A. 112;
B. 12;
C. 1;
D. 124.
Đáp án đúng là: B
Giáo viên chọn ngẫu nhiên 1 bạn lên bảng kiểm tra bài cũ. Ta có 2 biến cố:
A1 “Bạn được gọi là bạn nam”
A2 “Bạn được gọi là bạn nữ”
Do số bạn nữ bằng số bạn nam nên biến cố A1 và biến cố A2 có khả năng xảy ra như nhau hay hai biến cố có đồng khả năng. Mặt khác, cô chỉ gọi một bạn nên chỉ xảy ra một trong 2 biến cố này nên xác suất của mỗi biến cố bằng nhau và bằng 12.
Vậy biến cố “Bạn được gọi là bạn nam” có xác suất là 12.
Câu 5. Chọn ngẫu nhiên một trong 4 số 20; 22; 24 ; 26. Tìm xác suất để chọn được số chia hết cho 6.
A. 12;
B. 1;
C. 14;
D. 0.
Đáp án đúng là: C
Trong 4 số 20; 22; 24 ; 26 thì 24 là số chia hết cho 6. Do đó chọn được số chia hết cho 6 tức là chọn được số 24.
Vì chọn ngẫu nhiên 4 số nên 4 số có đồng khả năng.
Mặt khác, luôn chọn được duy nhất một trong bốn số trên nên xác suất chọn được một trong các số là bằng nhau và bằng 14.
Câu 6. Xác suất của biến cố nhận giá trị từ
A. 0 đến 1;
B. 1 đến 10;
C. 0 đến 10;
D. 1 đến 5.
Đáp án đúng là: A
Xác suất của biến cố nhận giá trị từ 0 đến 1, đây là con số biểu thị cho khả năng xảy ra của một biến cố.
Câu 7. Xác suất của một biến cố càng gần 1 thì biến cố đó càng …. khả năng xảy ra. Xác suất của một biến cố càng gần 0 thì biến cố đó càng …… khả năng xảy ra.
Từ thích hợp điền vào chỗ chấm lần lượt là
A. ít – nhiều;
B. nhiều – ít;
C. không có – có;
D. có – không có.
Đáp án đúng là: B
Xác suất của một biến cố càng gần 1 thì biến cố đó càng nhiều khả năng xảy ra. Xác suất của một biến cố càng gần 0 thì biến cố đó càng ít khả năng xảy ra.
Câu 8. Biến cố chắc chắn có xác suất là
A. 1;
B. 0;
C. một số bất kì;
D. Không xác định.
Đáp án đúng là: A
Khả năng xảy ra của biến cố chắc chắn là 100%. Vậy biến cố chắc chắn có xác suất bằng 1.
Câu 9. Trong một trò chơi hay thí nghiệm, nếu có k biến cố đồng khả năng và luôn xảy ra duy nhất một biến cố trong k biến cố này thì xác suất của mỗi biến cố đó đều bằng
A. k;
B. k – 1;
C. 1k;
D. k + 1.
Đáp án đúng là: C
Trong một trò chơi hay thí nghiệm, nếu có k biến cố đồng khả năng và luôn xảy ra duy nhất một biến cố trong k biến cố này thì xác suất của mỗi biến cố đó đều bằng 1k.
Câu 10. Cho hình vẽ. Quan sát hình và cho biết ngày có khả năng (xác suất) mưa ít nhất là
A. Ngày 04;
B. Ngày 05;
C. Ngày 06;
D. Ngày 07.
Đáp án đúng là: B
Biến cố có khả năng xảy ra thấp hơn sẽ có xác suất ít hơn.
Ta có: 24% < 44% < 48% < 50% < 76%.
Như vậy ngày 05 là ngày có khả năng (xác suất) mưa ít nhất.
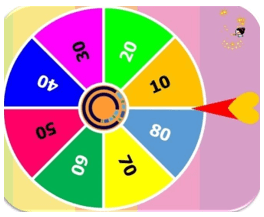
Câu 11. Một tấm bìa cứng hình tròn được gắn vào trục quay có mũi tên ở bên (hình vẽ). Bạn Mai quay tấm bìa. Biến cố “Mũi tên dừng ở hình quạt ghi số 20” có xác suất là
A. 120;
B. 18;
C. 180;
D. 12.
Đáp án đúng là: B
Vì tấm bìa được chia thành 8 hình quạt có điện tích bằng nhau nên 8 biến cố sau đồng khả năng.
“Mũi tên dừng ở hình quạt ghi số 10”
“Mũi tên dừng ở hình quạt ghi số 20”
“Mũi tên dừng ở hình quạt ghi số 30”
“Mũi tên dừng ở hình quạt ghi số 40”
“Mũi tên dừng ở hình quạt ghi số 50”
“Mũi tên dừng ở hình quạt ghi số 60”
“Mũi tên dừng ở hình quạt ghi số 70”
“Mũi tên dừng ở hình quạt ghi số 80”
Mặt khác luôn xảy ra duy nhất một trong 8 biến cố này.
Vậy xác suất của biến cố “Mũi tên dừng ở hình quạt ghi số 20” là 18.
Câu 12. Cho tập hợp A = {7; 10; 11; 14}. Chọn ngẫu nhiên một phần tử của tập hợp. Tìm xác suất của biến cố “Chọn được phần tử là số nguyên tố”.
A. 1;
B. 12;
C. 14;
D. 0.
Đáp án đúng là: B
Biến cố “Chọn được phần tử là số nguyên tố” xảy ra khi chọn được số 7 hoặc số 11.
Biến cố “Chọn được phần tử không là số nguyên tố” xảy ra khi chọn được số 10 hoặc số 14.
Vì hai biến cố này đều có 2 phần tử thỏa mãn nên 2 biến cố này đồng khả năng.
Và luôn xảy ra duy nhất một biến cố trong hai biến cố này nên xác suất của hai biến cố bằng nhau và bằng 12.
Vậy biến cố “Chọn được phần tử là số nguyên tố” có xác suất là 12.
Câu 13. Chọn ngẫu nhiên một số trong bốn số 5; 25; 20; x. Để biến cố “Chọn được số chia hết cho 5” có xác suất bằng 1 thì số x có thể là
A. 24;
B. 54;
C. 30;
D. 33.
Đáp án đúng là: C
Biến cố “Chọn được số chia hết cho 5” có xác suất bằng 1 thì biến cố này là biến cố chắc chắn.
Do đó cả 4 số 5; 25; 20; x đều phải chia hết cho 5.
Nên x chia hết cho 5.
Mà trong các đáp án đã cho, ta thấy chỉ 30 chia hết cho 5 nên x chỉ có thể là 30.
Câu 14. Nga viết tất cả các số có ba chữ số khác nhau từ các số chữ số 1; 2; 3 vào các tấm thẻ. Sau đó bạn Nga chọn ngẫu nhiên một tấm trong các tấm thẻ vừa viết. Xác suất của biến cố “Nga chọn được tấm thẻ ghi số 123” là
A. 13;
B. 1;
C. 16;
D. 14.
Đáp án đúng là: C
Các số có ba chữ số khác nhau được viết từ các số chữ số 1; 2; 3 là:
123; 132; 213; 231; 312; 321.
Vậy có tất cả 6 số ứng với 6 tấm thẻ.
Vì chọn ngẫu nhiên nên việc chọn được 1 trong 6 tấm thẻ là đồng khả năng.
Mà luôn chọn được duy nhất một số trong 6 số này.
Vậy xác suất của biến cố “Nga chọn được tấm thẻ ghi số 123” là 16.
Câu 15. Duy có 4 hộp bút với 4 màu: xanh, đỏ, tím, đen. Duy cho Hưng ngẫu nhiên một hộp. Xét các biến cố sau:
N1: “Duy cho Hưng hộp bút màu xanh”
N2: “Duy cho Hưng hộp bút màu tím”
N3: “Duy cho Hưng hộp bút màu vàng”
N4: “Duy cho Hưng hộp bút màu xanh hoặc đỏ hoặc tím hoặc đen”
Các biến cố có đồng khả năng là
A. N1 và N3;
B. N1 và N2;
C. N3 và N4;
D. N2 và N3.
Đáp án đúng là: B
Biến cố N3 là biến cố không thể nên không có khả năng xảy ra vì Duy không có hộp bút màu vàng.
Biến cố N4 là biến cố chắc chắn nên chắc chắn xảy ra.
Vì Duy có 4 hộp bút với 4 màu: xanh, đỏ, tím, đen và Duy cho Hưng ngẫu nhiên một hộp nên khả năng cho 1 trong 4 hộp là như nhau. Do đó biến cố N1 và N2 đồng khả năng.