Lý thuyết Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều (Chân trời sáng tạo 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

A. Lý thuyết Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Công thức tính diện tích xung quanh của hình chóp tam giác đều và hình chóp tứ giác đều

Diện tích xung quanh của hình chóp tam giác đều (hình chóp tứ giác đều) bằng tổng diện tích của các mặt bên.

Diện tích toàn phần của hình chóp tam giác đều (hình chóp tứ giác đều) bằng tổng của diện tích xung quanh và diện tích đáy:  ($S_{tp}=S_{xq}+S_{đáy}$ ($S_{tp}$ là diện tích toàn phần,  là diện tích đáy, $S_{xq}$ là diện tích xung quanh)

Công thức tính thể tích của hình chóp tam giác đều và hình chóp tứ giác đều

Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng $\frac{1}{3}$ diện tích đáy nhân với chiều cao.

$V=\frac{1}{3}{S}_{đáy}.h$. 

(V là thể tích, $S_{đáy}$ là diện tích đáy, $h$ là chiều cao)

Ví dụ:

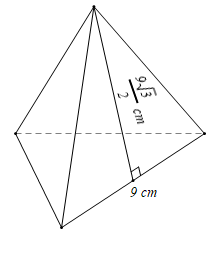
Cho hình chóp tứ giác đều sau:

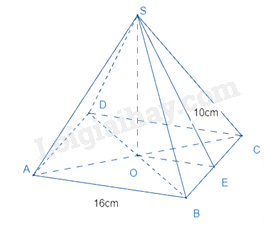
Diện tích xung quanh của hình chóp là: $S_{xq}=4.\frac{1}{2}.10.16=320(c{m}^2)$

Diện tích toàn phần của hình chóp là: $$S_{tp}=S_{xq}+S_{đáy}=320+16.16=576(c{m}^2)$$

Chiều cao của hình chóp là: $\sqrt{{10}^2-{\left(\frac{16}{2}\right)}^2}=\sqrt{100-64}=\sqrt{36}=6(cm)$

Thể tích của hình chóp là: $V=\frac{1}{3}.6.16.16=512(c{m}^3)$

B. Bài tập Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều

Bài 1.Cho hình chóp tứ giác đều A.BCDE có đáy là hình vuông cạnh 4 cm. Biết thể tích của hình chóp A.BCDE bằng 40 cm3. Tính độ dài đường cao của hình chóp?

Hướng dẫn giải

Áp dụng công thức tính thể tích của hình chóp tứ giác đều ta có

$V=\frac{1}{3}.S_{đáy}.h$

Suy ra $h=\frac{3V}{S_{đáy}}=\frac{3.40}{4^2}=7,5$(cm).

Bài 2.Cho hình chóp tứ giác đều có thể tích là 147 cm3, chiều cao của hình chóp là 9 cm. Tính chu vi đáy của hình chóp tứ giác đều đó.

Hướng dẫn giải

Áp dụng công thức tính thể tích của hình chóp tứ giác đều ta có:

$V=\frac{1}{3}.S_{đáy}.h$

Hay $147=\frac{1}{3}.S_{đáy}.\text{9}$

Suy ra Sđáy = 49 (cm2)

Do đó cạnh đáy của hình chóp tứ giác đều bằng $\sqrt{49}=7$ (cm).

Chu vi đáy là: 4.7 = 28 (cm).

Vậy chu vi đáy bằng 28 cm.

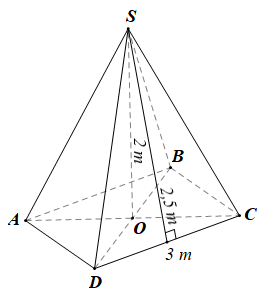
Bài 3.Trong dịp đi cắm trại, các bạn học sinh lớp 8 làm một chiếc lều trại hình chóp tứ giác đều có chiều cao 2 m, đáy là hình vuông cạnh 3 m, chiều cao của mỗi mặt bên của chiếc lều là 2,5 m.

a) Tính thể tích không khí bên trong lều.

b) Tính số mét vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp...).

Hướng dẫn giải

a) Thể tích không khí trong lều bằng thể tích lều và bằng:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}{.3}^2.2=6$(m3).

b) Số vải bạt cần thiết để dựng lều chính là diện tích xung quanh của lều.

Số mét vải bạt cần thiết để dựng lều là: ${\text{S}}_{xq}=4.\frac{1}{2}\mathrm{.3.2},5=15$ (m2).

Bài 4.

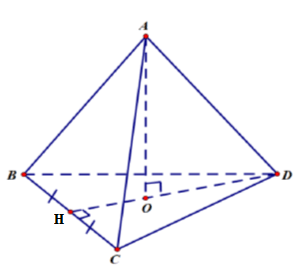
a) Tính diện tích xung quanh và diện tích toàn phần của hình chóp tam giác đều có tất cả các cạnh bằng 9 cm và chiều cao của tam giác mặt bên kẻ từ đỉnh của hình chóp bằng $\frac{9\sqrt{3}}{2}$ cm.

b) Tính thể tích của hình chóp A.BCD sau biết AO = 15 cm, BC = 10 cm, $DH=5\sqrt{3}$ cm.

Hướng dẫn giải

a)

Diện tích xung quanh của hình chóp tam giác đều đã cho là

$S_{xq}=3.\frac{1}{2}\mathrm{.9.}\frac{9\sqrt{3}}{2}=\frac{243\sqrt{3}}{4}$ (cm2).

Do hình chóp tam giác đều này có tất cả các cạnh bằng nhau nên tất cả các mặt là tam giác đều.

Diện tích đáy là

$S_{đáy}\text{=}\frac{1}{2}\mathrm{.9.}\frac{9\sqrt{3}}{2}=\frac{81\sqrt{3}}{4}$(cm2)

Diện tích toàn phần của hình chóp tam giác đều S.ABC là

${\text{S}}_{tp}{\text{= S}}_{xq}\text{+}{S}_{đáy}\text{=}\frac{243\sqrt{3}}{4}+\frac{81\sqrt{3}}{4}=81\sqrt{3}$(cm2).

b) Diện tích đáy là

$S_{đáy}\text{=}\frac{1}{2}\mathrm{.10.5}\sqrt{3}=25\sqrt{3}$(cm2)

Thể tích hình chóp tam giác đều đã cho là:

$V=\frac{1}{3}.S_{đáy}.h=\frac{1}{3}.25\sqrt{3}.15=125\sqrt{3}$(cm3).

Video bài giảng Toán 8 Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều - Chân trời sáng tạo