Lý thuyết Hình bình hành – Hình thoi (Chân trời sáng tạo 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 4: Hình bình hành – Hình thoi

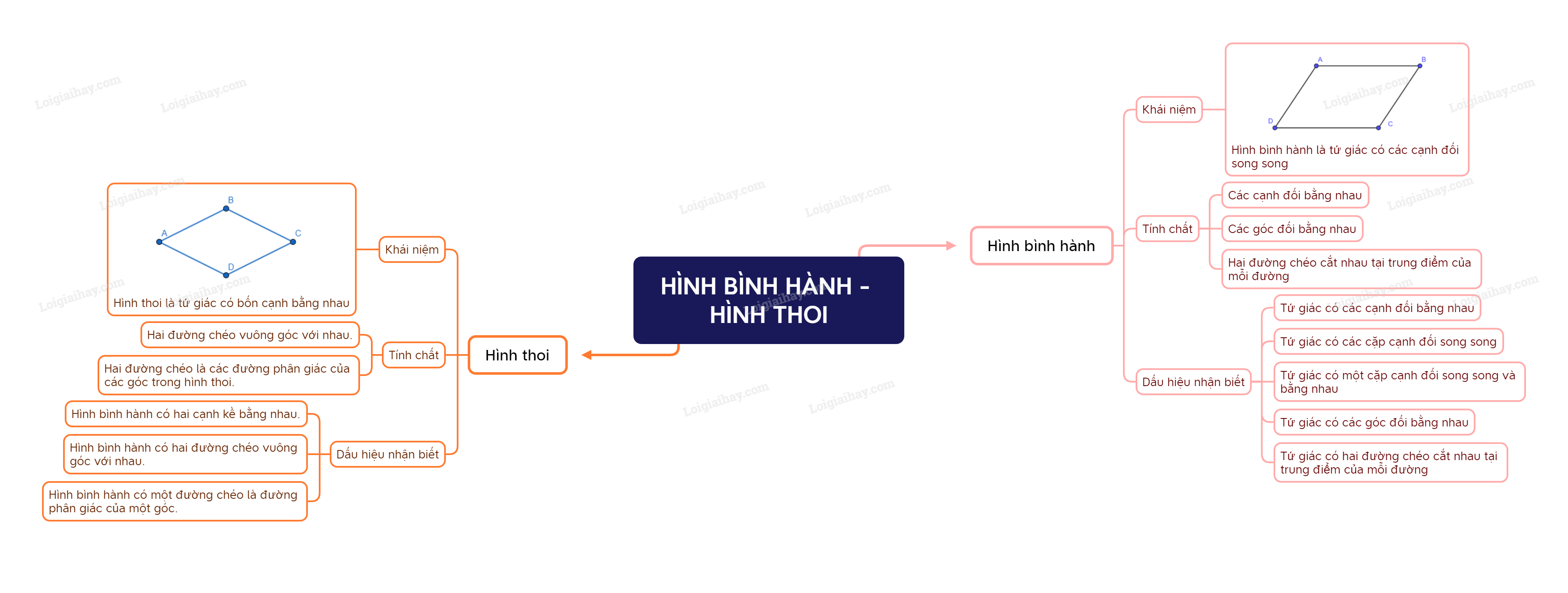
A. Lý thuyết Hình bình hành – Hình thoi

I. Hình bình hành

1. Khái niệm

Hình bình hành là tứ giác có các cạnh đối song song.

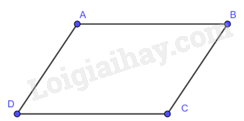
2. Hình bình hành có những tính chất gì?

Trong hình bình hành:

- Các cạnh đối bằng nhau;

- Các góc đối bằng nhau;

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết

- Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

- Tứ giác có các cặp cạnh đối song song là một hình bình hành.

- Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

- Tứ giác có các góc đối bằng nhau là một hình bình hành.

- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.

II. Hình thoi

1. Khái niệm

Hình thoi là tứ giác có bốn cạnh bằng nhau.

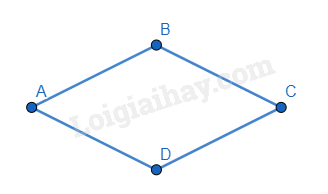
2. Tính chất

- Hai đường chéo vuông góc với nhau;

- Hai đường chéo là các đường phân giác của các góc trong hình thoi.

3. Dấu hiệu nhận biết hình thoi

- Hình bình hành có hai cạnh kề bằng nhau là hình thoi.

- Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.

- Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.

Ví dụ:

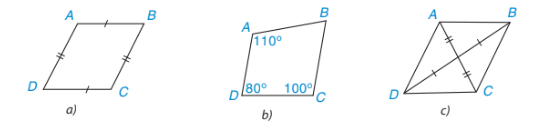
Hình a và c là hình bình hành do:

Hình a có các cặp cạnh đối bằng nhau.

Hình b có các đường chéo cắt nhau tại trung điểm của mỗi đường.

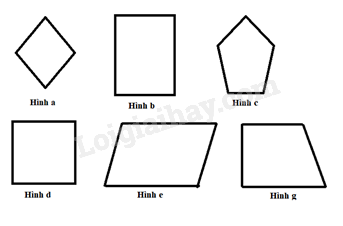
Hình a, d là hình thoi.

B. Bài tập Hình bình hành – Hình thoi

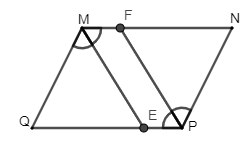
Bài 1. Cho hình bình hành MNPQ (MQ < MN). Từ M kẻ đường phân giác của $\widehat{QMN}$ cắt QP tại E, từ P kẻ đường phân giác của $\widehat{NPQ}$ cắt MN tại F.

a) Chứng minh ∆MQE là tam giác cân.

b) Tứ giác MEPF là hình gì? Tại sao?

Hướng dẫn giải

a) Ta có MNPQ là hình bình hành nên MN // PQ

Do đó $\widehat{QEM}=\widehat{EMN}$ (so le trong).

ME là đường phân giác của $\widehat{QMN}$ nên $\widehat{QME}=\widehat{EMN}=\frac{1}{2}\widehat{QMN}$

Suy ra .

Vậy tam giác MQE là tam giác cân tại Q.

b) Do ME là đường phân giác của $\widehat{NPQ}$ nên $\widehat{QME}=\widehat{EMN}=\frac{1}{2}\widehat{QMN}$

Do PF là đường phân giác của $\widehat{NPQ}$ nên $\widehat{NPF}=\widehat{QPF}=\frac{1}{2}\widehat{NPQ}$

Mà $\widehat{QMN}=\widehat{NPQ}$ (hai góc đối của hình bình hành)

Suy ra $\widehat{EMN}=\widehat{QPF}$ hay $\widehat{EMF}=\widehat{EPF}$ .

Mặt khác, MN // PQ nên $\widehat{EMF}=\widehat{MEQ}$ (so le trong)

Do đó $\widehat{MEQ}=\widehat{EPF}$ , mà hai góc này ở vị trí so le trong nên ME // PF

Xét tứ giác MEPF có ME // PF và MF // PE nên là hình bình hành.

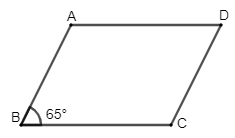
Bài 2. Hình bình hành ABCD có $\hat{B}=65°$. Tính các góc A, C, D.

Hướng dẫn giải

ABCD là hình bình hành nên ta có: và (tính chất hình bình hành)

Áp dụng định lí tổng các góc của một tứ giác ta có: $\hat{A}+\hat{B}+\hat{C}+\hat{D}=360°$

Suy ra $2\hat{A}=360°-2\hat{B}=360°-2.65°=230°$.

Do đó $\hat{A}=\hat{C}=\frac{230°}{2}=115°$.

Vậy $\hat{A}=\hat{C}=115°$và $\hat{D}=65°$ .

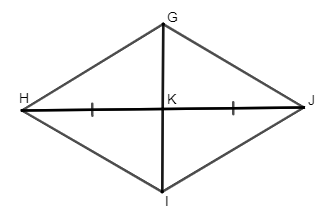
Bài 3. Cho tam giác GHJ cân tại G. Đường trung tuyến kẻ từ G của tam giác cắt HJ tại K. Lấy điểm I trên tia GK sao cho KG = KI. Chứng minh GHIJ là hình thoi.

Hướng dẫn giải

• Ta có GK là trung tuyến của tam giác GHJ nên K là trung điểm của HJ.

Do KG = KI nên K là trung điểm của GI.

Tứ giác GHIJ có hai đường chéo GI và HJ cắt nhau tại trung điểm K của mỗi đường nên là hình bình hành.

• ∆GHJ cân tại G nên đường trung tuyến GK đồng thời là đường cao tương ứng với cạnh HJ nên GI ⊥ HJ.

Hình bình hành GHIJ có hai đường chéo GI và HJ vuông góc với nhau nên là hình thoi.

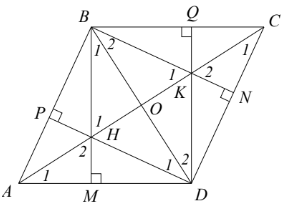
Bài 4. Cho hình thoi ABCD có B là góc tù. Từ B hạ BM ⊥ AD, BN ⊥ CD. Từ D hạ DP ⊥ AB, DQ ⊥ BC. Gọi H là giao điểm của MB và PD, K là giao điểm của BN và DQ, O là giao điểm của AC và BD.

a) Chứng minh H là trực tâm của tam giác ABD.

b) Chứng minh A, H, K, C thẳng hàng.

c) Chứng minh $\widehat{PDQ}=\widehat{MBN}$ .

d) Chứng minh $\widehat{PHM}=\widehat{QKN}$ .

e) Chứng minh tứ giác BHDK là hình thoi.

Hướng dẫn giải

a) Tam giác ABD có hai đường cao BM, DP cắt nhau tại H nên H là trực tâm của tam giác.

b) ABCD là hình thoi nên AC ⊥ BD tại O, do đó A, O, C thẳng hàng (1)

Do H là trực tâm của DABD suy ra AH ⊥ BD tại O nên H ∈ AO (2)

Chứng minh tương tự câu a ta có K là trực tâm DBCD

Suy ra CK ⊥ BD tại O nên K ∈ CO (3)

Từ (1), (2) và (3) suy ra A, H, K, C thẳng hàng.

c) Vì ABCD là hình thoi nên hai đường chéo AC, BD vuông góc với nhau tại trung điểm của mỗi đường

Suy ra AC là đường trung trực của BD

Do đó HB = HD nên DHBD cân tại H, suy ra ${\hat{B}}_1={\hat{D}}_1$

Tương tự, ${\hat{B}}_2={\hat{D}}_2$

Suy ra ${\hat{B}}_1+{\hat{B}}_2={\hat{D}}_1+{\hat{D}}_2$ hay $\widehat{MBN}=\widehat{PDQ}$.

d) ABCD là hình thoi nên $\widehat{BAD}=\widehat{BCD}$

Tứ giác APHM có $\widehat{PHM}=360°-90°-90°-\widehat{BAD}$

Tứ giác CQKN có $\widehat{QKN}=360°-90°-90°-\widehat{BCD}$

Suy ra $\widehat{PHM}=\widehat{QKN}$ .

e) Ta có: ${\hat{A}}_1+{\hat{H}}_2=90°$ và ${\hat{C}}_1+{\hat{K}}_2=90°$

Mà ${\hat{A}}_1={\hat{C}}_1$ nên ${\hat{H}}_2={\hat{K}}_2$

Lại có ${\hat{H}}_1={\hat{H}}_2$ (đối đỉnh) và ${\hat{K}}_1={\hat{K}}_2$ (đối đỉnh) nên ${\hat{H}}_1={\hat{K}}_1$

Suy ra DBHK cân tại B, nên BH = BK

Mà BH = DH và BK = DK nên BH = HD = CK = KB

Suy ra tứ giác BHDK là hình thoi.

Video bài giảng Toán 8 Bài 4: Hình bình hành – Hình thoi - Chân trời sáng tạo