Lý thuyết Phương trình bậc nhất một ẩn (Chân trời sáng tạo 2024) Toán 8
Tóm tắt lý thuyết Toán 8 Bài 1: Phương trình bậc nhất một ẩn ngắn gọn, chính xác sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 8.
Lý thuyết Toán lớp 8 Bài 1: Phương trình bậc nhất một ẩn
A. Lý thuyết Phương trình bậc nhất một ẩn
1. Phương trình một ẩn
Một phương trình với ẩn x có dạng , trong đó vế trái A(x) và vế phải B(x) là hai biểu thức có cùng một biến x.
Ví dụ: là các phương trình ẩn x.
Giá trị của biến làm cho hai vế của phương trình có giá trị bằng nhau gọi là nghiệm của phương trình đó.
Ví dụ: là nghiệm của phương trình vì thay vào phương trình, ta được 2.2 = 2 + 2
2. Phương trình bậc nhất một ẩn
Khái niệm:
Phương trình dạng ax + b = 0, với a và b là hai số đã cho và , được gọi là phương trình bậc nhất một ẩn.
Việc tìm các nghiệm của một phương trình gọi là giải phương trình đó.
Cách giải:
Phương trình bậc nhất ax + b = 0 () được giải như sau:
(chuyển b từ vế trái sang vế phải và đổi dấu thành –b)
(chia hai vế cho a)
Vậy phương trình có nghiệm .
Ví dụ: Giải phương trình:
Ta có:
Vậy nghiệm của phương trình là .
Chú ý: Quá trình giải phương trình có thể dẫn đến trường hợp đặc biệt là hệ số của ẩn bằng 0. Khi đó, phương trình có thể không có nghiệm (vô nghiệm) hoặc nghiệm đúng với mọi x.
Sơ đồ tư duy Phương trình bậc nhất một ẩn
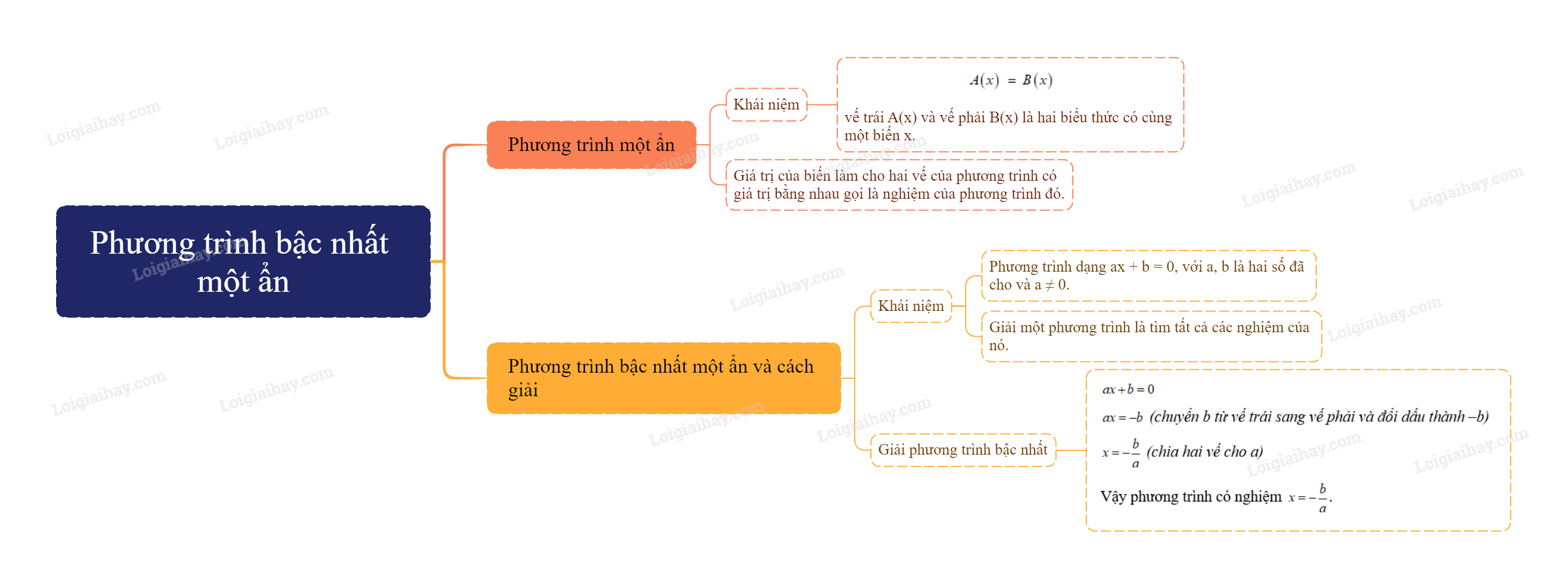
B. Bài tập Phương trình bậc nhất một ẩn
Đang cập nhật...