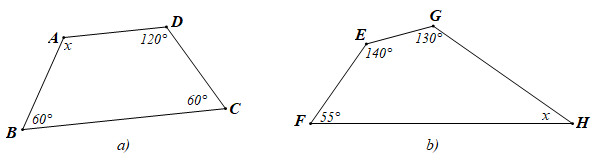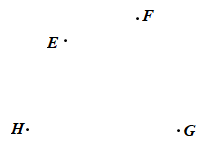Tóm tắt lý thuyết Toán 8 Bài 2: Tứ giác ngắn gọn, chính xác sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 8.
Lý thuyết Toán lớp 8 Bài 2: Tứ giác A. Lý thuyết Tứ giác 1. Khái niệm Tứ giác
Ví dụ:
Đặc điểm
+ Có 4 đỉnh
+ Có 4 cạnh
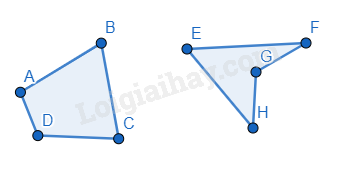
Tứ giác lồi
Ví dụ: ABCD là tứ giác lồi, EFGH không phải là tứ giác lồi.
2. Tính chất + Hai cạnh kề nhau là hai cạnh chung đỉnh.
+ Hai cạnh kề nhau tạo thành góc của tứ giác.
+ Hai cạnh đối nhau không chung đỉnh.
+ Hai đỉnh đối nhau là hai đỉnh không cùng nằm trên một cạnh.
+ Đường chéo là đoạn thẳng nối hai đỉnh đối nhau.
3. Định lí tổng các góc của một tứ giác Tổng số đo các góc của một tứ giác bằng 360 0 360 0
Tứ giác ABCD, ˆ A + ˆ B + ˆ C + ˆ D = 360 0 A ^ + B ^ + C ^ + D ^ = 360 0
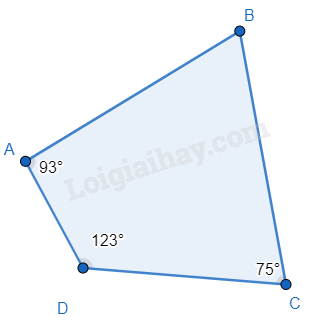
Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Ví dụ:
ˆ B = 360 0 − 93 0 − 123 0 − 75 0 = 69 0 Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span
B. Bài tập Tứ giác Bài 1. Tính x trong mỗi hình sau:
Hướng dẫn giải
a) Theo định lí tổng các góc của một tứ giác, trong tứ giác ABCD có:
ˆ A + ˆ B + ˆ C + ˆ D = 360 o Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span x = 360 o − ( 60 o + 60 o + 120 o ) = 360 o − 240 o = 120 o
Suy ra x = ˆ A = 360 o − ( ˆ B + ˆ C + ˆ D ) x = A ^ = 360 o − B ^ + C ^ + D ^
Vậy x = 120 o x = 120 o .
b) Theo định lí tổng các góc của một tứ giác, trong tứ giác EGHF có: ˆ E + ˆ G + ˆ H + ˆ F = 360 o E ^ + G ^ + H ^ + F ^ = 360 o
Suy ra x = ˆ H = 360 o − ( ˆ E + ˆ G + ˆ F ) x = H ^ = 360 o − E ^ + G ^ + F ^
x = 360 o − ( 140 o + 130 o + 55 o ) = 360 o − 325 o = 35 o x = 360 o − 140 o + 130 o + 55 o = 360 o − 325 o = 35 o
Vậy x = 35 o x = 35 o
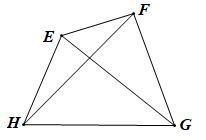
Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Bài 2. Cho bốn điểm E, F, G, H (hình vẽ).
Vẽ một tứ giác có các đỉnh là bốn điểm đã cho và tìm các yếu tố sau:
a) cạnh kề, cạnh đối của cạnh GH.
b) góc đối của ˆ E F G E F G ^ .
c) hai đường chéo của tứ giác.
Hướng dẫn giải
a) Cạnh kề của cạnh GH là cạnh GF; cạnh đối của cạnh GH là cạnh EF.
b) Góc đối của ˆ E F G E F G ^ là ˆ E H G E H G ^
c) Hai đường chéo của tứ giác là EG và FH.
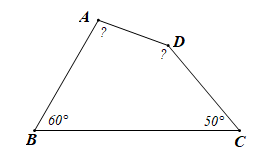
Bài 3. Tứ giác ABCD có ˆ C = 50 ° Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span ; ˆ B = 60 ° Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span ; ˆ A − ˆ B = 40 ° Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span . Tính số đo các góc A và D.
Hướng dẫn giải
Theo giả thiết: ˆ A − ˆ B = 40 o Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span nên ˆ A = 40 o + ˆ B = 40 o + 60 o = 100 o Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span
Theo định lí tổng các góc của một tứ giác, trong tứ giác ABCD có:
ˆ A + ˆ B + ˆ C + ˆ D = 360 o Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span
Suy ra ˆ D = 360 o − ( ˆ B + ˆ C + ˆ A ) Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span ⎛ ⎝ Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span ⎞ ⎠ Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span
ˆ D = 360 o − ( 60 o + 50 o + 100 o ) = 360 o − 210 o = 150 o Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span ( Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span ) Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span
Vậy ˆ A = 100 o ; ˆ D = 150 o Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span Unknown node type: span
VIDEO
Video bài giảng Toán 8 Bài 2: Tứ giác