Câu hỏi:
89 lượt xemCho hình hộp ABCD.A’B’C’D’, gọi G là trọng tâm của tam giác BDA’.
a) Biểu diễn theo và .
b) Từ câu a, hãy chứng tỏ ba điểm A, G và C’ thẳng hàng.
Lời giải
Hướng dẫn giải:
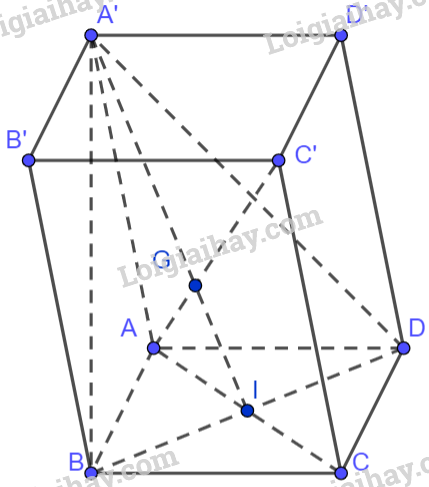
Gọi I là giao điểm của AC và BD. Vì tứ giác ABCD là hình bình hành nên I là trung điểm của BD. Do đó, A’I là đường trung tuyến của tam giác A’BD. Mà G là trọng tâm tam giác A’BD nên .
Vì I là trung điểm BD nên:
Do đó,
Ta có:
b) Vì ABCD.A’B’C’D’ là hình hộp nên
Do đó, nên hai vectơ và cùng phương. Vậy ba điểm A, G và C’ thẳng hàng.
Cho hình hộp ABCD.A’B’C’D’. Khẳng định nào dưới đây là sai?
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho . Khẳng định nào dưới đây là sai?
A. .
B. .
C. .
D. .
Trong không gian Oxyz, cho . Tích vô hướng bằng
A. .
B. .
C. 11.
D. 2.
Trong không gian Oxyz, cho . Góc giữa hai vectơ bằng
A. .
B. .
C. .
D. .
Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật. Chứng minh rằng: .
Cho tứ diện ABCD, lấy hai điểm M, N thỏa mãn và . Hãy biểu diễn theo và .

