Câu hỏi:
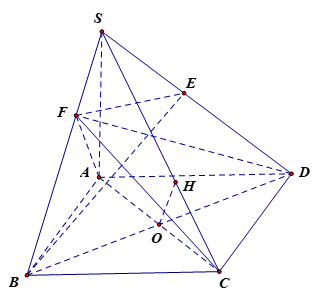
238 lượt xemCho hình chóp S.ABCD có SA (ABCD), biết ABCD là hình vuông cạnh bằng a và SA = a .
a) Chứng minh rằng (SAC) (SBD) và (SAD) (SCD).
b) Gọi BE, DF là hai đường cao của tam giác SBD. Chứng minh rằng (ACF) (SBC) và (AEF) (SAC).
c) Tính theo a khoảng cách giữa hai đường thẳng BD và SC.
Lời giải
Hướng dẫn giải:
a) Ta có ABCD là hình vuông nên AC BD. Mà SA (ABCD) nên SA BD.
Do đó BD (SAC) mà BD (SBD) nên (SAC) (SBD).
Vì ABCD là hình vuông nên AD CD mà SA (ABCD) nên CD SA.
Do đó CD (SAD) mà CD (SCD) nên (SAD) (SCD).
b) Vì ABCD là hình vuông nên AD AB mà SA (ABCD) nên AD SA.
Do đó AD (SAB), suy ra AD SB.
Vì DF là đường cao của tam giác SBD nên SB DF mà AD SB do đó SB (ADF), suy ra SB AF.
Vì ABCD là hình vuông nên AB BC, mà SA (ABCD) nên SA BC.
Do đó BC (SAB) nên BC AF.
Có SB AF và BC AF, do đó AF (SBC) mà AF (ACF) nên (ACF) (SBC).
Vì AF (SBC) nên AF SC.
Vì CD (SAD), suy ra CD AE.
Vì ABCD là hình vuông nên AD AB mà SA (ABCD) nên AB SA.
Vì AD AB và AB SA nên AB (SAD), suy ra AB SD.
Lại có BE là đường cao của tam giác SBD nên BE SD.
Vì AB SD và BE SD nên SD (ABE), suy ra SD AE.
Vì SD AE mà CD AE nên AE (SCD), suy ra AE SC mà AF SC.
Do đó SC (AEF) mà SC (SAC) nên (AEF) (SAC).
c) Gọi O là giao điểm của AC và BD, kẻ OH SC tại H.
Có AC BD và BD SA nên BD (SAC), suy ra OH BD.
Do đó OH là đoạn vuông góc chung của BD và SC hay d(BD, SC) = OH.
Xét tam giác ABC vuông tại B, có AC = .
Do ABCD là hình vuông nên O là trung điểm của AC nên OC = .
Xét tam giác SAC vuông tại A nên SC =
Xét CHO và CAS có góc C chung và nên CHO đồng dạng với CAS, suy ra .
Vậy d(BD, SC) = .