Câu hỏi:
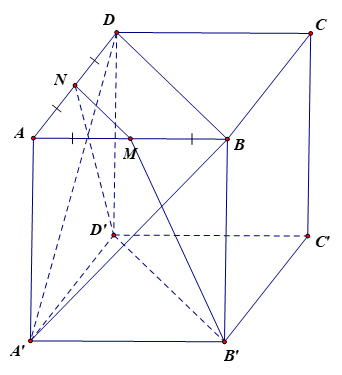
262 lượt xemCho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD.
a) Tính theo a thể tích khối chóp cụt AMN.A'B'D'.
b) Tính theo a khoảng cách giữa hai đường thẳng MN và A'B.
Lời giải
Hướng dẫn giải:
a) Ta có mà ABCD và A'B'C'D' là hình vuông nên .
Vì M, N lần lượt là trung điểm của AB, AD nên .
Xét AMN và ABD có góc A chung và nên AMN đồng dạng với ABD.
Suy ra .
(Ngoài cách trên, ta có thể tính được AM = AN = , suy ra .AM.AN = )
Khi đó
.
b) Xét tam giác ABD có M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác ABD. Do đó MN // BD. Suy ra MN // (A'BD).
Do đó d(MN, A'B) = d(MN, (A'BD)) = d(M, (A'BD)).
Vì M là trung điểm của AB nên d(M,(A'BD)) = d(A,(A'BD)).
Đặt h = d(A, (A'BD)).
Áp dụng kết quả bài 7.7 trang 28 SBT Toán 11 tập 2, ta có:
.
Vậy d(MN,A'B) =