Câu hỏi:
105 lượt xem Tự luận
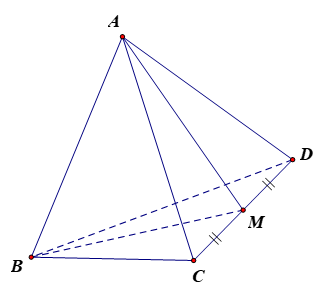
Cho tứ diện đều ABCD có cạnh bằng a, côsin của góc giữa hai mặt phẳng (ACD) và (BCD) bằng
A. .
B. .
C. .
D. .
Lời giải
Hướng dẫn giải:
Đáp án đúng là: D
Gọi M là trung điểm của CD.
Do tam giác ACD và BCD là tam giác đều nên AM CD và BM CD.
Khi đó góc giữa hai mặt phẳng (ACD) và (BCD) bằng góc giữa hai đường thẳng AM và BM, mà (AM,BM) = .
Vì tam giác ACD và BCD là tam giác đều cạnh bằng a nên AM = BM = .
Áp dụng định lí côsin cho tam giác ABM có:
.
Vậy côsin góc giữa hai mặt phẳng (ACD) và (BCD) bằng .
Câu 1:
Câu 3:
Câu 4:
Câu 6:
Câu 7:
Câu 8:
Câu 9:
Câu 10:
Câu 11:
Câu 12:
Câu 13:
Câu 14:
Câu 15: