Câu hỏi:
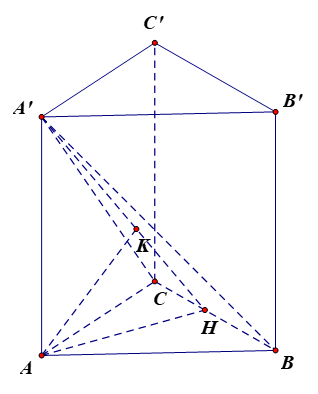
369 lượt xemCho hình lăng trụ đứng ABC.A'B'C' có , AB = 2a, AC = 3a và số đo của góc nhị diện [A', BC, A] bằng 45°.
a) Tính theo a khoảng cách từ điểm A đến mặt phẳng (A'BC).
b) Tính theo a thể tích khối lăng trụ ABC.A'B'C'.
Lời giải
Hướng dẫn giải:
a) Kẻ AH BC tại H.
Vì ABC.A'B'C' là lăng trụ đứng nên A'A (ABC), suy ra A'A BC mà AH BC nên BC (A'AH).
Kẻ AK A'H tại K, lại có BC AK (do BC (A'AH)) nên AK (A'CB).
Do đó d(A, (A'BC)) = AK.
Có BC (A'AH) nên BC A'H mà AH BC nên góc nhị diện [A', BC, A] bằng , suy ra .
Áp dụng định lí côsin trong tam giác ABC, có
- 2.AB.AC.cos = 4a2+9a2-2.2a.3a.cos60o = 7a2.
BC = a.
Vì
= .
Xét tam giác AHK vuông tại K, có AK = AH . sin45° = .
Vậy d(A, (A'BC)) = .
b) Vì tam giác A'AH vuông tại A, nên tam giác A'AH vuông cân tại A nên AA' = AH = .
Ta có: AA' = .AB.AC.sin.AA'
= .2a.3a.sin60o.= .