Câu hỏi:
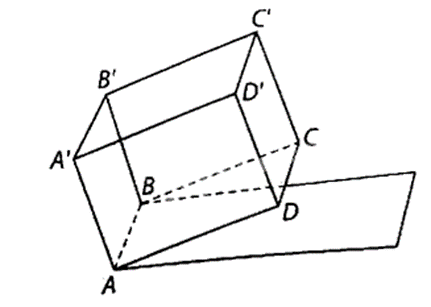
173 lượt xemMột bể chứa nước hình hộp chữ nhật ABCD.A'B'C'D' được đặt trên một mái nhà nghiêng so với mặt đất nằm ngang góc 10°, AB = 1 m, AD = 1,5 m, AA' = 1 m. Đáy bể là hình chữ nhật ABCD. Các điểm A, B cùng ở độ cao 5 m (so với mặt đất), các điểm C, D ở độ cao lớn hơn so với độ cao của các điểm A, B. Khi nước trong bể phẳng lặng người ta đo được khoảng cách giữa đường mép nước ở mặt phẳng (ABB'A') và mặt đáy của bể là 80 cm. Tính thể tích của phần nước trong bể.
Lời giải
Hướng dẫn giải:
Gọi MN là đường mép nước ở trên mặt (ABB'A'), EF là đường mép nước trên mặt (CDD'C'). Khi đó ABNM.DCEF là một hình chóp cụt. Kẻ MH DD' tại H. Khi đó ADHM là hình chữ nhật nên MH = AD = 1,5 m, AM = DH = 80 cm = 0,8 m.
Xét tam giác MHF vuông tại H, (do mái nhà nghiêng so với mặt đất nằm ngang góc 10° và MF song song với mặt đất), có: HF = MH × tan10° = 1,5tan10° (m).
Suy ra DF = DH – HF = AM – HF = 0,8 – 1,5tan10° 0,54 (m).
Do DCEF là hình chữ nhật nên S1 = SDCEF = DF × CD = DF ∙ AB 0,54 (m2);
Do ABNM là hình chữ nhật nên S2 = SABNM = AB × AM = 0,8 (m2).
Thể tích phần nước trong bể là:
.
Vậy thể tích nước trong bể khoảng 1 m3.