Cho hình vẽ biết , và vuông góc với nhau,
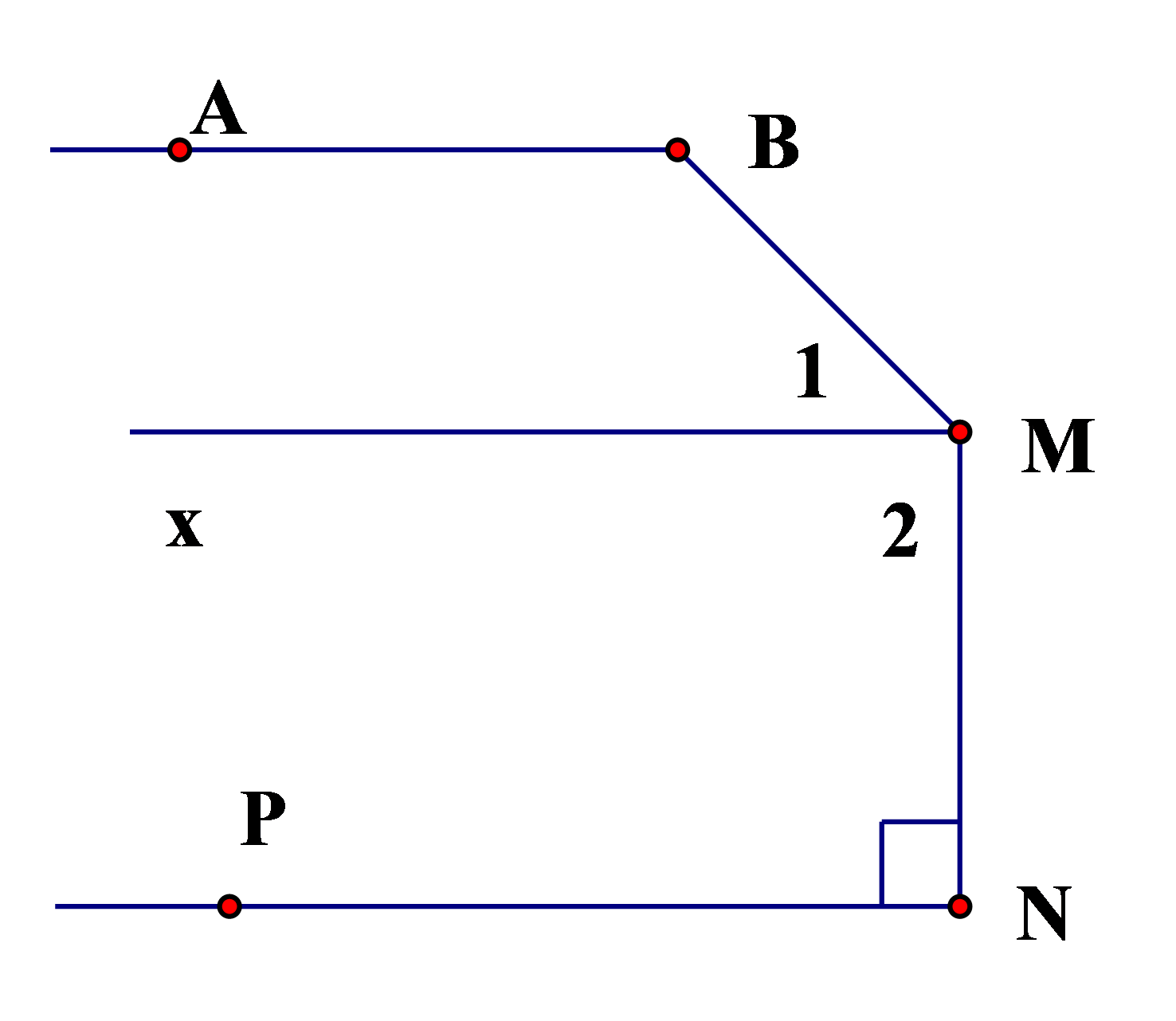
1) Tính số đo các góc .
2) Chứng minh: .
3) Kẻ tia phân giác của , cắt tia tại điểm . Chứng minh: .
Hướng dẫn giải:
GT, KL: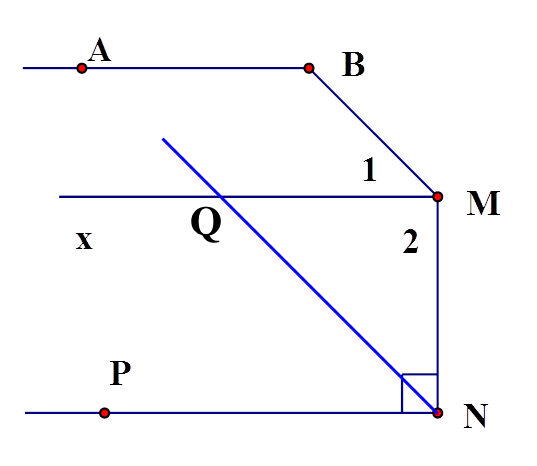
Để làm ý 1,2 HS không cần thiết phải vẽ hình
1) Ta có: Þ
Hay Þ
Vì ÞÞ
2) Vì Þ
Mà (gt)
Nên (vì cùng vuông góc với )
Do đó (vì cùng song song với ).
3) Vì MQ là tia phân giác của
Þ Þ
Vì Þ (cặp góc so le trong)
Þ Þ (đpcm)
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 2
Tùng, Huy và Minh cùng trồng hoa cúc trong chậu để bán dịp tết. Tùng trồng được 6 chậu hoa, Huy trồng được 4 chậu hoa và Minh trồng được 5 chậu hoa. Ba bạn bán hết hoa thu được tổng số tiền là 1,5 triệu đồng. Ba bạn quyết định chia tiền tỉ lệ với số chậu hoa trồng được. Tính số tiền mỗi bạn nhận được?
Hướng dẫn giải:
Gọi số tiền ba bạn Tùng, Huy và Minh nhận được lần lượt là (triệu đồng)
Vì tổng số tiền ba bạn nhận được khi bán hết chậu hoa là triệu đồng nên ta có: .
Vì số tiền mỗi bạn nhận được tỉ lệ với số chậu hoa trồng được nên ta có: .
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
Suy ra:
(thỏa mãn)
Vậy số tiền bạn Tùng, Huy và Minh nhận được lần lượt là: 0,6 triệu đồng, 0,4 triệu đồng, 0,5 triệu đồng.
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 2
và
a) Chứng minh
b) Tính số đo
a) Chứng minh
b) Chứng minh và
c) Gọi là trung điểm của đoạn thẳng
Chứng minh ba điểm là ba điểm thẳng hàng.
(Ý 2.c học sinh vẽ thêm hình vào hình trên.)
Hướng dẫn giải:
1)
a) Ta có ,
(định lý)
b)
Vì (hai góc so le trong)
Vì (hai góc kề bù)
2)
a)
Xét và có:
(gt)
(gt)
chung
b)
+) Ta có (hai góc kề bù)
(hai góc kề bù)
mà (cmt)
+) Vì (cmt) (hai góc tương ứng)
+) Ta có
+) Xét và có:
(cmt)
(cmt)
(cmt)
Do đó (g.c.g)
c)
+) Lập luận được là tia phân giác
+) Lập luận được là tia phân giác
Tia trùng với tia
Ba điểm là ba điểm thẳng hàng.
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 1
1) Kết quả tìm hiểu về khả năng tự nấu ăn của các bạn lớp 7A được cho bởi bảng sau:
|
Khả năng tự nấu ăn |
Không đạt |
Đạt |
Giỏi |
Xuất sắc |
|
Số bạn nữ tự đánh giá |
|
|
|
|
a) Trong hai dãy dữ liệu trên, dãy nào là dãy số liệu? Dãy nào không là dãy số liệu?
b) Dữ liệu trên có đại diện cho khả năng tự nấu ăn của các bạn lớp 7A được không? Tại sao?
2) Ngày 12/12/2022, An khảo sát dự đoán của tất cả các bạn trong lớp 7B về đội vô địch World cup 2022 của bốn đội vào vòng Tứ kết (mỗi bạn chỉ được chọn một đội); thu được kết quả như sau:
|
Đội bóng |
Argentina |
Croatia |
Morocco |
Pháp |
|
Số bạn dự đoán |
|
|
|
|
a) Tính số bạn tham gia cuộc khảo sát.
b) Tính tỉ lệ các bạn trong lớp 7B dự đoán đội vô địch World cup 2022 của bốn đội trên.
c) Hoàn thiện biểu đồ sau để biểu diễn kết quả dự đoán đội vô địch World cup 2022.
(Học sinh vẽ trực tiếp vào biểu đồ dưới đây.)
Hướng dẫn giải:
1)
a) Dãy số liệu là: số bạn nữ tự đánh giá nấu ăn (không đạt, đạt, giỏi và xuất sắc):
Dãy dữ liệu không là số liệu là: Khả năng nấu ăn: không đạt, đạt, giỏi, xuất sắc.
b) Dữ liệu trên không đại diện cho khả năng tự nấu ăn của các bạn học sinh lớp 7A được.
Vì các dữ liệu trên chỉ được thu thập từ việc khảo sát các bạn nữ.
2)
a)
Số bạn tham gia cuộc khảo sát là:
(bạn)
b)
Tỉ lệ phần trăm các bạn lớp 7B dự đoán đội Argentina vô địch là:
Tỉ lệ phần trăm các bạn lớp 7B dự đoán đội Croatia vô địch là:
Tỉ lệ phần trăm các bạn lớp 7B dự đoán đội Morocco vô địch là:
Tỉ lệ phần trăm các bạn lớp 7B dự đoán đội Pháp vô địch là:
c)
Tô màu hoặc đánh dấu đúng các hình quạt.
Tên biểu đồ và Chú thích đúng.
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 1
Lan làm thí nghiệm đun nước tinh khiết trong điều kiện bình thường và đo nhiệt độ của nước tại một số thời điểm sau khi bắt đầu đun được kết quả như sau:
|
Số phút sau khi bắt đầu đun |
|
|
|
|
|
|
|
|
Nhiệt độ |
|
|
|
|
|
|
|
Giá trị nào không hợp lý trong dữ liệu về nhiệt độ của nước mà Lan thu được ?
Đề thi học kì 1 Toán 7 KNTT có đáp án - Đề 1
Cho hình vẽ bên:
a) Viết tên hai cặp góc đối đỉnh, hai cặp góc so le trong.
b) Chứng minh .
c) Cho Tính số đo .
Hướng dẫn giải:
a) (1,0 điểm)
Các cặp góc đối đỉnh: và ; và ; và ; và .
Các cặp góc so le trong: và ; và .
b) (1,0 điểm)
Ta có và là hai góc so le trong.
Mà nên (dấu hiệu nhận biết hai đường thẳng song song).
c) (1,0 điểm)
Ta có (hai góc kề bù)
Vậy .
Đề thi giữa kì 1 Toán 7 KNTT có đáp án - Đề 5 có đáp án
a) Tìm , biết: .
b) Tính hợp lí: .
c) So sánh và .
d) Cho biết 1 inch ≈ 2,54 cm. Tìm độ dài đường chéo màn hình tivi 48 inch đơn vị cm và làm tròn đến hàng phần chục.
Hướng dẫn giải:
a) (0,5 điểm)
b) (0,5 điểm)
c) (0,5 điểm)
• ;
• .
.
d) (0,5 điểm)
Đường chéo là: (cm).
Vậy đường chéo làm tròn đến phần chục là cm.
Đề thi giữa kì 1 Toán 7 KNTT có đáp án - Đề 5 có đáp án
Trong các câu sau câu nào không cho một định lí?
Đề thi giữa kì 1 Toán 7 KNTT có đáp án - Đề 5 có đáp án