Lý thuyết Hình bình hành (Cánh diều 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 4: Hình bình hành

A. Lý thuyết Hình bình hành

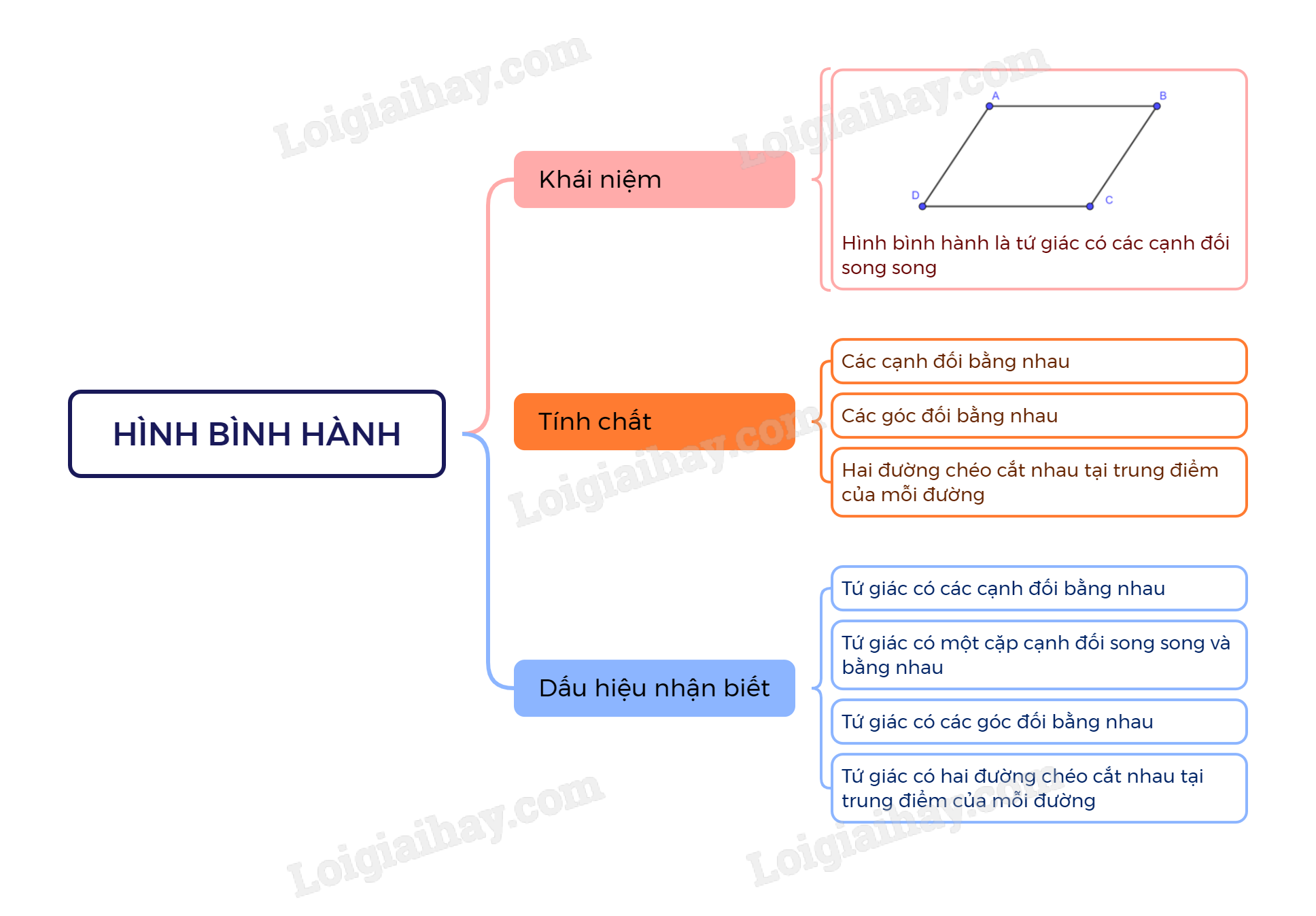
1. Khái niệm

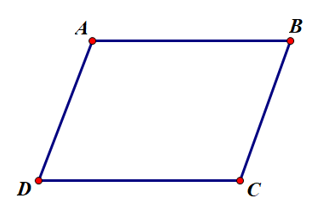
Hình bình hành là tứ giác có các cạnh đối song song.

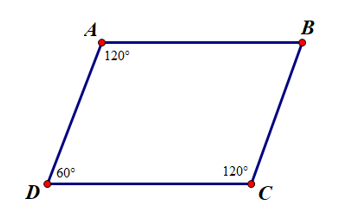
Ví dụ: Cho hình vẽ, tứ giác ABCD có phải là hình bình hành không? Vì sao?

Hướng dẫn giải

Tứ giác ABCD có: $\widehat{A}+\widehat{D}=120°+60°=180°$

Mà hai góc ở vị trí trong cùng phía

Suy ra AB // CD    (1)

Lại có: $\widehat{C}+\widehat{D}=120°+60°=180°$

Mà hai góc ở vị trí trong cùng phía

Suy ra AD // BC    (2)

Từ (1) và (2) suy ra ABCD là hình bình hành.

2. Tính chất

Trong hình bình hành:

- Các cạnh đối bằng nhau;

- Các góc đối bằng nhau;

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

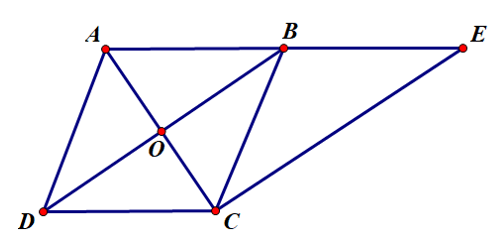
Ví dụ: Cho hai hình bình hành ABCD và BECD, AC cắt BD tại O. Chứng minh:

a) AB = BE;

b) $OB=\frac{1}{2}CE$ .

Hướng dẫn giải

Do ABCD là hình bình hành nên:

AB = CD, $OB=OD=\frac{1}{2}BD$ .

Do BECD là hình bình hành nên BE = CD, BD = CE.

a) Từ AB = CD và BE = CD, suy ra AB = BE (vì cùng bằng CD).

Vậy AB = BE.

b) Từ $OB=\frac{1}{2}BD$  và BD = CE.

Do đó $OB=\frac{1}{2}CE$ .

3. Dấu hiệu nhận biết

- Tứ giác có các cạnh đối bằng nhau là một hình bình hành.

- Tứ giác có một cặp cạnh đối song song và bằng nhau là một hình bình hành.

- Tứ giác có các góc đối bằng nhau là một hình bình hành.

- Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là một hình bình hành.

Ví dụ: 

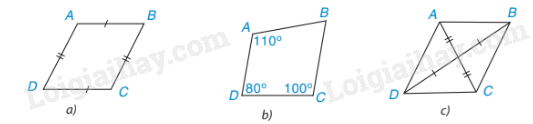
Hình a và c là hình bình hành do:

Hình a có các cặp cạnh đối bằng nhau.

Hình b có các đường chéo cắt nhau tại trung điểm của mỗi đường.

B. Bài tập Hình bình hành

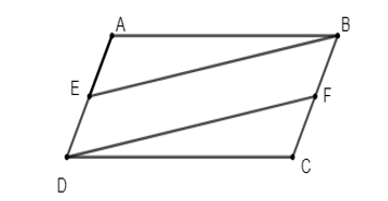
Bài 1. Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh:

a) BE = DF;

b) BE // DF.

Hướng dẫn giải

Vì E là trung điểm của AD, F là trung điểm của BC nên:

 $AE=DE=\frac{1}{2}AD$ và $\text{BF}=\text{CF}=\frac{1}{2}AD$

Mà AD = BC nên AE = CF.

Xét ΔABE và ΔCDF có:

AB = DC

$\widehat{\text{EAB}}=\widehat{\text{DCF}}$ (Vì ABCD là hình bình hành)

AE = CF

Suy ra ΔABE = ΔCDF (c.g.c)

Suy ra BE = DF.

Vậy BE = DF.

b) Xét tứ giác EBFD có: BE = DF và DE = BF

Suy ra tứ giác EBFD là hình bình hành.

Do đó BE // DF.

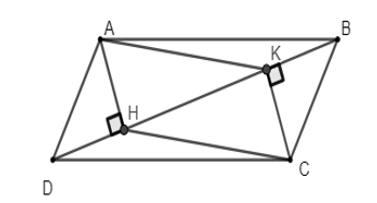
Bài 2. Cho hình bình hành ABCD, đường chéo BD. Kẻ AH và CK vuông góc với BD lần lượt tại H và K. Chứng minh tứ giác AHCK là hình bình hành.

Hướng dẫn giải

Vì tứ giác ABCD là hình bình hành nên: AD = BC và AD // BC.

Vì AD // BC nên $\widehat{ADH}=\widehat{CBK}$  (hai góc so le trong).

Ta có: $\text{AH}\perp \text{BD}$  và $\text{CK}\perp \text{BD}$ . Suy ra: $\widehat{\text{AHD}}=\widehat{\text{CKB}}=90°$  và AH // CK.

Xét ΔAHD và ΔCKB có:

$\widehat{\text{AHD}}=\widehat{\text{CKB}}=90°$

$\widehat{\text{ADH}}=\widehat{\text{CBK}}$

AD = BC (cmt)

Do đó ΔAHD = ΔCKB (cạnh huyền – góc nhọn)

Suy ra AH = CK (hai cạnh tương ứng)

Xét tứ giác AHCK có:

AH = CK và AH // CK

Vậy tứ giác AHCK là hình bình hành.