Lý thuyết Mặt phẳng tọa độ. Đồ thị của hàm số (Cánh diều 2024) Toán 8
Tóm tắt lý thuyết Toán 8 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số ngắn gọn, chính xác sách Cánh diều sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 8.
Lý thuyết Toán lớp 8 Bài 2: Mặt phẳng tọa độ. Đồ thị của hàm số
A. Lý thuyết Mặt phẳng tọa độ. Đồ thị của hàm số
1. Mặt phẳng tọa độ
Trên mặt phẳng, ta vẽ hai trục số Ox, Oy vuông góc với nhau và cắt nhau tại gốc O của mỗi trục. Khi đó ta có trục tọa độ Oxy.
Trục Ox, Oy gọi là các trục tọa độ. Ox là trục hoành, Oy là trục tung. O là gốc tọa độ.
Mặt phẳng có hệ trục tọa độ Oxy gọi là mặt phẳng Oxy.
Chú ý. Các đơn vị độ dài trên hai trục tọa độ được chọn bằng nhau.
2. Tọa độ của một điểm trong mặt phẳng tọa độ
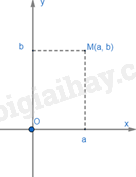
Cho điểm M nằm trong mặt phẳng tọa độ.
Giả sử hình chiếu của điểm M lên Ox là điểm a, lên Oy là điểm b. Cặp số (a;b) gọi là tọa độ của điểm M, a là hoành độ, b là tung độ.
Điểm M có tọa độ (a; b) kí hiệu là M(a; b).
3. Độ thị của hàm số
Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x;f(x)) trên mặt phẳng tọa độ.
Ví dụ: Xét hàm số y = 2x
Giá trị y1;y2 tương ứng với x1=−1;x2=1 là: y1=2.(−1)=−2;y2=2.1=2
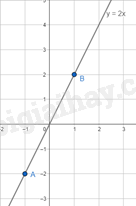
Hàm số y = 2x có đồ thị như sau:

B. Bài tập Mặt phẳng tọa độ. Đồ thị của hàm số
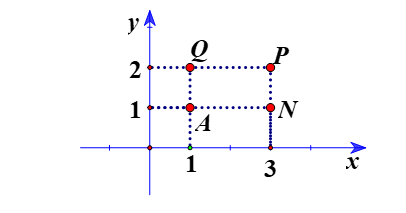
Bài 1: Viết tọa độ các điểm A, N, P, Q trong hình bên dưới.
Hướng dẫn giải
Cách xác định:
- Từ điểm đã cho kẻ đường thẳng song song với trục tung, cắt trục hoành tại một điểm biểu diễn hoành độ của điểm đó.
- Từ điểm đã cho kẻ đường thẳng song song với trục hoành, cắt trục tung tại một điểm biểu diễn tung độ của điểm đó.
- Hoành độ và tung độ tìm được là tọa độ của điểm đã cho.
Từ đó, ta các định được tọa độ các điểm là: A(1; 1), N(3; 1), P(3; 2), Q(1; 2).
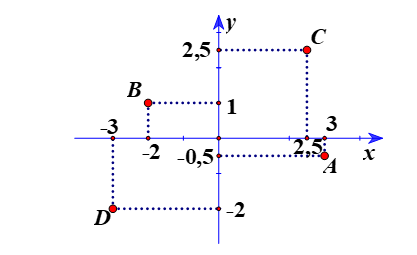
Bài 2: Vẽ mặt phẳng tọa độ Oxy và đánh dấu vị trí các điểm sau trên đó A(3; −0,5), B(−2; 1), C(2,5; 2,5), D(−3; −2).
Hướng dẫn giải
Cách xác định:
- Từ điểm biểu diễn hoành độ của điểm cho trước, kẻ một đường thẳng song song với trục tung.
- Tử điểm biểu diễn tung độ của điểm cho trước, kẻ một đường thẳng song song với trục hoành.
- Giao điểm của hai đường thẳng vừa dựng là điểm phải tìm.