Lý thuyết Hình vuông (Cánh diều 2024) Toán 8

Lý thuyết Toán lớp 8 Bài 7: Hình vuông

A. Lý thuyết Hình vuông

1. Khái niệm

Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

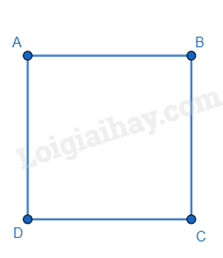
2. Tính chất

- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường

- Hai đường chéo là các đường phân giác của các góc ở đỉnh.

3. Dấu hiệu nhận biết hình vuông

- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.

- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

- Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông.

Ví dụ:

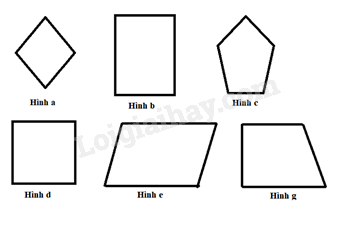
Hình d là hình vuông

B. Bài tập Hình vuông

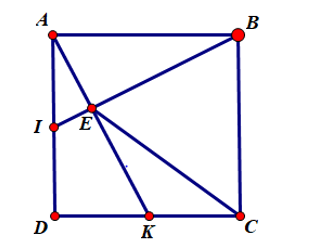
Bài 1. Cho hình vuông ABCD. Gọi I, K lần lượt là trung điểm của AD và DC.

a) Chứng minh rằng BI ⊥ AK.

b) Gọi E là giao điểm của BI và AK. Chứng minh rằng $\widehat{EBC}=\widehat{EKD}$ .

Hướng dẫn giải

Xét ∆BAI và ∆ADK có:

AB = AD

$AI=DK=\frac{1}{2}AB=\frac{1}{2}DA$

$\widehat{A}=\widehat{D}$

Suy ra ∆BAI = ∆ADK  (c.g.c)

Suy ra $\widehat{ABI}=\widehat{DAK}$  (góc tương ứng bằng nhau)

Mà $\widehat{IAE}+\widehat{EAB}=90°$

Suy ra $\widehat{ABI}+\widehat{EAB}=90°$

• Xét ∆ABE có $\widehat{EAB}+\widehat{ABE}+\widehat{AEB}=180°$

Suy ra $\widehat{AEB}=180°-\left(\widehat{ABE}+\widehat{BAE}\right)=180°-90°=90°$

Hay AK ⊥ BI (đpcm)

• Xét tứ giác EBCK có $\widehat{KEB}+\widehat{EBC}+\widehat{BCK}+\widehat{CKE}=360°$

Suy ra $\widehat{EBC}+\widehat{EKC}=180°$

Mà $\widehat{AKD}+\widehat{AKC}=180°$ .

Do đó $\widehat{EBC}=\widehat{EKD}$ .

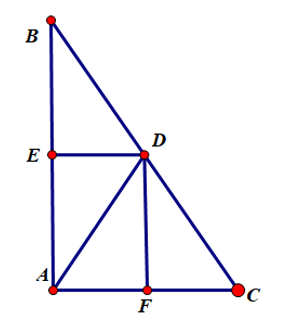
Bài 2. Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.

Hướng dẫn giải

Xét tứ giác AEDF có:

$\widehat{A}=\widehat{E}=\widehat{F}=90°$

Suy ra AEDF là hình chữ nhật (1)

Theo giả thiết ta có: AD là đường phân giác của góc $\widehat{\text{A}}$ .

Suy ra $\widehat{\text{EAD}}=\widehat{\text{DAF}}=45°$ .

Xét ΔAED có: $\widehat{\text{AED}}=90°$

$\widehat{\text{EAD}}=45°$

Suy ra $\widehat{\text{EDA}}=45°$ .

Suy ra ΔAED vuông cân tại E nên AE = ED (2).

Từ (1) và (2) suy ra AEDF là hình vuông.

Vậy AEDF là hình vuông.