Vận dụng trang 74 Toán 10 Tập 2:
a) Dùng hai số hạng đầu tiên trong khai triển của (1 + 0,05)4 để tính giá trị gần đúng của 1,054.
b) Dùng máy tính cầm tay tính giá trị của 1,054 và tính sai số tuyệt đối của giá trị gần đúng nhận được ở câu a.
Giải Toán 10 (Kết nối tri thức) Bài 25: Nhị thức Newton
Giải Toán 10 trang 74 Tập 2
Hoạt động 4 trang 74 Toán 10 Tập 2: Tương tự như HĐ3, sau khi khai triển (a + b)5, ta thu được một tổng gồm 25 đơn thức có dạng x . y . z . t . u, trong đó mỗi kí hiệu x, y, z, t, u là a hoặc b. Chẳng hạn, nếu x, z là a, còn y, t, u là b thì ta có đơn thức a . b . a . b . b, thu gọn là a2b3. Để có đơn thức này, thì trong 5 nhân tử x, y, z, t, u có 3 nhân tử là b, 2 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a2b3 trong tổng là .
Lập luận tương tự như trên, dùng kiến thức về tổ hợp, hãy cho biết, trong tổng nhận được nêu trên có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:
• a5; • a4b; • a3b2; • a2b3; •ab4; •b5.
Giải Toán 10 (Kết nối tri thức) Bài 25: Nhị thức Newton
Giải Toán 10 trang 73 Tập 2
Hoạt động 3 trang 73 Toán 10 Tập 2: Sơ đồ hình cây của khai triển (a + b)4 được mô tả như Hình 8.9. Sau khi khai triển, ta thu được một tổng gồm 24 (theo quy tắc nhân) đơn thức có dạng x . y . z . t, trong đó mỗi x, y, z, t là a hoặc b. Chẳng hạn, nếu x, y, t là a, còn z là b thì ta có đơn thức a . a . b . a, thu gọn là a3b. Để có đơn thức này, thì trong 4 nhân tử x, y, z, t có 1 nhân tử là b, 3 nhân tử còn lại là a. Khi đó số đơn thức đồng dạng với a3b trong tổng là .
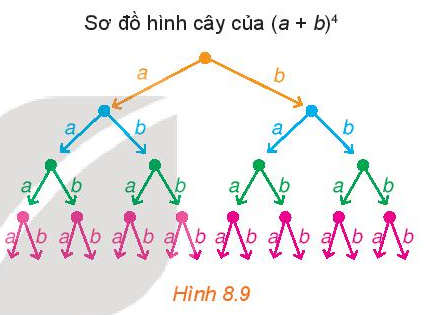
Lập luận tương tự trên, dùng kiến thức về tổ hợp, hãy cho biết trong tổng nêu trên, có bao nhiêu đơn thức đồng dạng với mỗi đơn thức thu gọn sau:
• a4; • a3b; • a2b2; • ab3; • b4.
Giải Toán 10 (Kết nối tri thức) Bài 25: Nhị thức Newton
Hoạt động 2 trang 72 Toán 10 Tập 2: Hãy cho biết các đơn thức còn thiếu (...) trong sơ đồ hình cây (H.8.7) của tích (a + b) . (a + b) . (a + b).
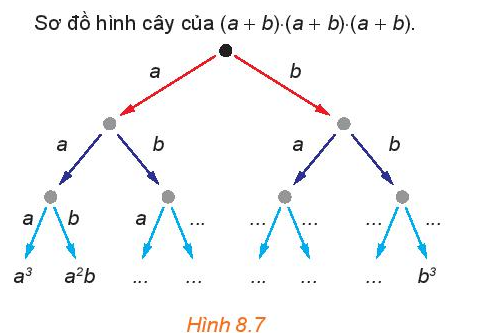
Có bao nhiêu tích nhận được lần lượt bằng a3, a2b, ab2, b3?
Hãy so sánh chúng với các hệ số nhận được khi khai triển (a + b)3.
Giải Toán 10 (Kết nối tri thức) Bài 25: Nhị thức Newton
Hoạt động 1 trang 72 Toán 10 Tập 2: Sơ đồ hình cây của tích hai nhị thức (a + b) . (c + d) được xây dựng như sau:
• Từ một điểm gốc, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức (gọi là nhãn của mũi tên) của nhị thức thứ nhất (H.8.6);
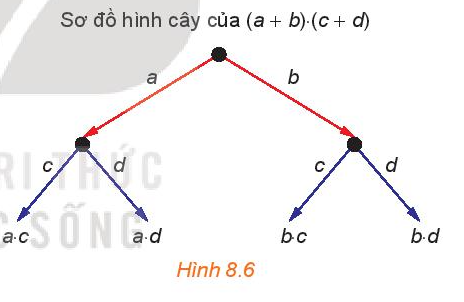
• Từ ngọn của mỗi mũi tên đã xây dựng, kẻ các mũi tên, mỗi mũi tên tương ứng với một đơn thức của nhị thức thứ hai;
• Tại ngọn của các mũi tên xây dựng tại bước sau cùng, ghi lại tích của các nhãn của các mũi tên đi từ điểm gốc đến đầu mút đó.
Hãy lấy tổng của các tích nhận được và so sánh kết quả với khai triển của tích (a + b) . (c + d).
Giải Toán 10 (Kết nối tri thức) Bài 25: Nhị thức Newton
Giải bài tập Toán 10 Bài 25: Nhị thức Newton
A. Các câu hỏi trong bài
Giải Toán 10 trang 72 Tập 2
Mở đầu trang 72 Toán 10 Tập 2: Ở lớp 8, khi học về hằng đẳng thức, ta đã biết khai triển: (a + b)2 = a2 + 2ab + b2; (a + b)3 = a3 + 3a2b + 3ab2 + b3.
Quan sát các đơn thức ở vế phải của các đẳng thức trên, hãy nhận xét về quy luật số mũ của a và b. Có thể tìm được cách tính các hệ số của đơn thức trong khai triển (a + b)n khi n ∈ {4; 5} không?
Giải Toán 10 (Kết nối tri thức) Bài 25: Nhị thức Newton
Giải Toán 10 trang 70 Tập 2
Vận dụng trang 70 Toán 10 Tập 2: Một câu lạc bộ có 20 học sinh.
a) Có bao nhiêu cách chọn 6 thành viên vào Ban quản lí?
b) Có bao nhiêu cách chọn Trưởng ban, 1 Phó ban, 4 thành viên khác vào Ban quản lí?
Giải Toán 10 (Kết nối tri thức) Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Giải Toán 10 trang 71 Tập 2
Bài 8.10 trang 71 Toán 10 Tập 2: Một câu lạc bộ cờ vua có 10 bạn nam và 7 bạn nữ. Huấn luyện viên muốn chọn 4 bạn đi thi đấu cờ vua.
a) Có bao nhiêu cách chọn 4 bạn nam?
b) Có bao nhiêu cách chọn 4 bạn không phân biệt nam, nữ?
c) Có bao nhiêu cách chọn 4 bạn, trong đó có 2 bạn nam và 2 bạn nữ?
Giải Toán 10 (Kết nối tri thức) Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Giải Toán 10 trang 69 Tập 2
Luyện tập 3 trang 69 Toán 10 Tập 2: Trong ngân hàng đề kiểm tra cuối học kì II môn Vật lí có 20 câu lí thuyết và 40 câu bài tập. Người ta chọn ra 2 câu lí thuyết và 3 câu bài tập trong ngân hàng đề để tạo thành một đề thi. Hỏi có bao nhiêu cách lập đề thi gồm 5 câu hỏi theo cách chọn như trên?
Giải Toán 10 (Kết nối tri thức) Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Giải Toán 10 trang 68 Tập 2
Luyện tập 2 trang 68 Toán 10 Tập 2: Trong một giải đua ngựa gồm 12 con ngựa, người ta chỉ quan tâm đến 3 con ngựa: con nhanh nhất, nhanh nhì và nhanh thứ ba. Hỏi có bao nhiêu kết quả có thể xảy ra?
Giải Toán 10 (Kết nối tri thức) Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Hoạt động 2 trang 67 Toán 10 Tập 2: Trong lớp 10T có bốn bạn Tuấn, Hương, Việt, Dung tham gia cuộc thi hùng biện của trường. Hỏi có bao nhiêu cách chọn:
a) Hai bạn phụ trách nhóm từ bốn bạn?
b) Hai bạn phụ trách nhóm, trong đó một bạn làm nhóm trưởng, một bạn làm nhóm phó?
Giải Toán 10 (Kết nối tri thức) Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Hoạt động 1 trang 66 Toán 10 Tập 2: Một nhóm gồm bốn bạn Hà, Mai, Nam, Đạt xếp thành một hàng, từ trái sang phải, để tham gia một cuộc phỏng vấn.

a) Hãy liệt kê ba cách sắp xếp bốn bạn trên theo thứ tự.
b) Có bao nhiêu cách sắp xếp thứ tự bốn bạn trên để tham gia phỏng vấn?
Giải Toán 10 (Kết nối tri thức) Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Giải bài tập Toán 10 Bài 24: Hoán vị, chỉnh hợp và tổ hợp
A. Các câu hỏi trong bài
Giải Toán 10 trang 66 Tập 2
Mở đầu trang 66 Toán 10 Tập 2: Danh sách các cầu thủ của Đội tuyển bóng đá quốc gia tham dự một trận đấu quốc tế có 23 cầu thủ gồm 3 thủ môn, 7 hậu vệ, 8 tiền vệ và 5 tiền đạo. Huấn luyện viên rất bí mật, không cho ai biết đội hình (danh sách 11 cầu thủ) sẽ ra sân. Trong cuộc họp báo, ông chỉ tiết lộ đội sẽ đá theo sơ đồ 3 – 4 – 3 (nghĩa là 3 hậu vệ, 4 tiền vệ, 3 tiền đạo và 1 thủ môn). Đối thủ đã có danh sách 23 cầu thủ (tên và vị trí của từng cầu thủ) và rất muốn dự đoán đội hình, họ xét hết các khả năng có thể xảy ra. Hỏi nếu đối thủ đã dự đoán trước vị trí thủ môn thì họ sẽ phải xét bao nhiêu đội hình có thể?
Giải Toán 10 (Kết nối tri thức) Bài 24: Hoán vị, chỉnh hợp và tổ hợp
Bài 8.5 trang 65 Toán 10 Tập 2: a) Mật khẩu của chương trình máy tính quy định gồm 3 kí tự, mỗi kí tự là một chữ số. Hỏi có thể tạo được bao nhiêu mật khẩu khác nhau?
b) Nếu chương trình máy tính quy định mới mật khẩu vẫn gồm 3 kí tự, nhưng kí tự đầu tiên phải là một chữ cái in hoa trong bảng chữ cái tiếng Anh gồm 26 chữ (từ A đến Z) và 2 kí tự sau là các chữ số (từ 0 đến 9). Hỏi quy định mới có thể tạo được nhiều hơn quy định cũ bao nhiêu mật khẩu khác nhau?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Bài 8.3 trang 65 Toán 10 Tập 2: Ở một loài thực vật, A là gene trội quy định tính trạng hoa kép, a là gene lặn quy định tính trạng hoa đơn.
a) Sự tổ hợp giữa hai gene trên tạo ra mấy kiểu gene? Viết các kiểu gene đó.
b) Khi giao phối ngẫu nhiên, có bao nhiêu kiểu giao phối khác nhau từ các kiểu gene đó?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
B. Bài tập
Bài 8.1 trang 65 Toán 10 Tập 2: Trên giá sách có 8 cuốn truyện ngắn, 7 cuốn tiểu thuyết và 5 tập thơ (tất cả đều khác nhau). Vẽ sơ đồ hình cây minh hoạ và cho biết bạn Phong có bao nhiêu cách chọn một cuốn để đọc vào ngày cuối tuần.
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Giải Toán 10 trang 65 Tập 2
Vận dụng trang 65 Toán 10 Tập 2: Khối lớp 10 của một trường trung học phổ thông có ba lớp 10A, 10B, 10C. Lớp 10A có 30 bạn, lớp 10B có 35 bạn, lớp 10C có 32 bạn. Nhà trường muốn chọn 4 bạn để thành lập đội cờ đỏ của khối sao cho có đủ đại diện của các lớp. Hỏi có bao nhiêu cách lựa chọn?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Giải Toán 10 trang 64 Tập 2
Luyện tập 2 trang 64 Toán 10 Tập 2: Tại kì World Cup năm 2018, vòng bảng gồm có 32 đội tham gia, được chia vào 8 bảng, mỗi bảng 4 đội thi đấu vòng tròn (mỗi đội chơi một trận với từng đội khác trong cùng bảng). Hỏi tổng cộng vòng bảng có bao nhiêu trận đấu?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Giải Toán 10 trang 63 Tập 2
Hoạt động 4 trang 63 Toán 10 Tập 2: Để lắp ghế vào một phòng chiếu phim, các ghế được gắn nhãn bằng một chữ cái in hoa (trong bảng 26 chữ cái tiếng Anh từ A đến Z) đứng trước và một số nguyên từ 1 đến 20, chẳng hạn X15, Z2,...
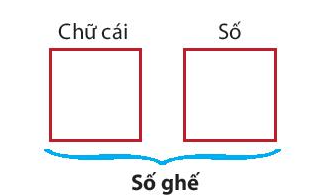
Hỏi có thể gắn nhãn tối đa được bao nhiêu ghế?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Hoạt động 3 trang 62 Toán 10 Tập 2: Thầy Trung muốn đi từ Hà Nội vào Huế, rồi từ Huế vào Quảng Nam. Biết rằng từ Hà Nội vào Huế có thể đi bằng 3 cách: ô tô, tàu hỏa hoặc máy bay. Còn từ Huế vào Quảng Nam có thể đi bằng 2 cách: ô tô hoặc tàu hỏa (H.8.5).
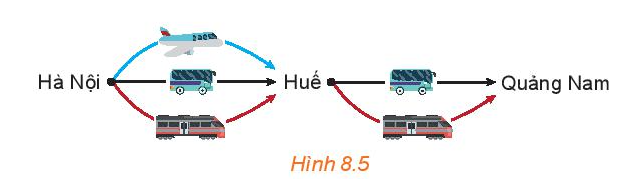
Hỏi thầy Trung có bao nhiêu cách chọn các phương tiện để đi từ Hà Nội vào Quảng Nam?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Hoạt động 2 trang 61 Toán 10 Tập 2: Chọn vé tàu (H.8.2)
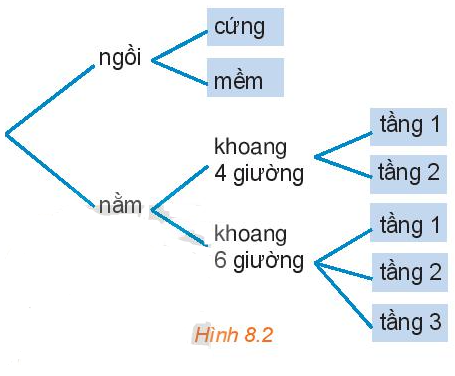
Bạn An đã quyết định mua vé tàu đi từ Hà Nội vào Vinh trên chuyến tàu SE7. Trên tàu có các toa ghế ngồi và các toa giường nằm. Toa ngồi có hai loại vé: ngồi cứng và ngồi mềm. Toa nằm có loại khoang 4 giường và khoang 6 giường. Khoang 4 giường có hai loại vé: tầng 1 và tầng 2, khoang 6 giường có ba loại vé: tầng 1, tầng 2 và tầng 3. Hỏi:
a) Có bao nhiêu loại vé ghế ngồi và bao nhiêu loại vé giường nằm?
b) Có bao nhiêu loại vé để bạn An lựa chọn?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Giải Toán 10 trang 61 Tập 2
Hoạt động 1 trang 61 Toán 10 Tập 2: Chọn chuyến đi (H.8.1)
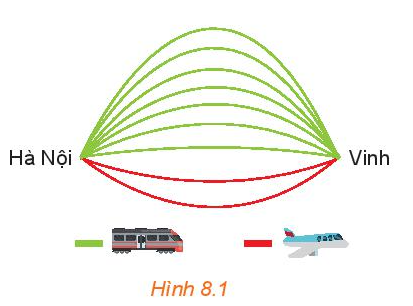
Từ Hà Nội vào Vinh mỗi ngày có 7 chuyến tàu hỏa và 2 chuyến máy bay. Bạn An muốn ngày Chủ nhật này đi từ Hà Nội vào Vinh bằng tàu hỏa hoặc máy bay. Hỏi bạn An có bao nhiêu cách chọn chuyến đi?
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Giải bài tập Toán 10 Bài 23: Quy tắc đếm
A. Các câu hỏi trong bài
Giải Toán 10 trang 60 Tập 2
Mở đầu trang 60 Toán 10 Tập 2: Đếm là một bài toán cổ xưa nhất của nhân loại. Trong khoa học và trong cuộc sống, người ta cần đếm các đối tượng để giải quyết các vấn đề khác nhau. Chẳng hạn như bài toán sau:
Mỗi mật khẩu của một trang web là một dãy có từ 2 tới 3 kí tự, trong đó kí tự đầu tiên là một trong 26 chữ cái in thường trong bảng chữ cái tiếng Anh (từ a đến z), mỗi kí tự còn lại là một chữ số từ 0 đến 9. Hỏi có thể tạo được bao nhiêu mật khẩu khác nhau?
Bài học này sẽ giúp em hiểu và áp dụng hai quy tắc đếm cơ bản để giải quyết bài toán trên.
Giải Toán 10 (Kết nối tri thức) Bài 23: Quy tắc đếm
Bài 7.37 trang 59 Toán 10 Tập 2: Một cột trụ hình hyperbol (H.7.36), có chiều cao 6m, chỗ nhỏ nhất ở chính giữa và rộng 0,8m, đỉnh cột và đáy cột đều rộng 1m. Tính độ rộng của cột ở độ cao 5m (Tính theo đơn vị mét và làm tròn tới hai chữ số sau dấu phẩy).
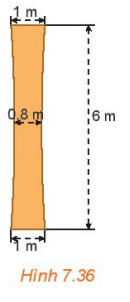
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 7
Bài 7.36 trang 59 Toán 10 Tập 2: Cho hypebol có phương trình :
a) Tìm các giao điểm A1, A2 của hypebol với trục hoành (hoành độ của A1 nhỏ hơn của A2).
b) Chứng minh rằng, nếu điểm M(x; y) thuộc nhánh nằm bên trái trục tung của hypebol thì x ≤ –a, nếu điểm M(x; y) thuộc nhánh nằm bên phải trục tung của hypebol thì x ≥ a.
c) Tìm các điểm M1, M2 tương ứng thuộc các nhánh bên trái, bên phải trục tung của hyperbol để M1M2 nhỏ nhất.
Giải Toán 10 (Kết nối tri thức) Bài tập cuối chương 7