Bài 5.26 trang 90 Toán 10 Tập 1: Tỉ lệ trẻ em suy dinh dưỡng (tính theo cân nặng tương ứng với độ tuổi) của 10 tỉnh thuộc Đồng bằng sông Hồng được cho như sau:

5,5   13,8   10,2   12,2   11,0   7,4   11,4   13,1    12,5   13,4.

(Theo Tổng cục Thống kê)

a) Tính số trung bình, trung vị, khoảng biến thiên và độ lệch chuẩn của mẫu số liệu trên.

b) Thực hiện làm tròn đến hàng đơn vị cho các giá trị trong mẫu số liệu. Sai số tuyệt đối của phép làm tròn này không vượt quá bao nhiêu?

Bài 5.25 trang 90 Toán 10 Tập 1: Hai mẫu số liệu sau đây cho biết số lượng trường Trung học phổ thông ở mỗi tỉnh/thành phố thuộc Đồng bằng sông Hồng và Đồng bằng sông Cửu Long năm 2017:

Đồng bằng sông Hồng: 187  34   35   46   54    57   37   39   23   57   27.

Đồng bằng sông Cửu Long: 33   34   33   29   24   39   42   24   23   19   24   15   26.

(Theo Tổng cục Thống kê)

a) Tính số trung bình, trung vị, các tứ phân vị, mốt, khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn cho mỗi mẫu số liệu trên.

b) Tại sao số trung bình của hai mẫu số liệu có sự sai khác nhiều trong khi trung vị thì không?

c) Tại sao khoảng biến thiên và độ lệch chuẩn của hai mẫu số liệu khác nhau nhiều trong khi khoảng tứ phân vị thì không?

Giải Toán 10 trang 90 Tập 1

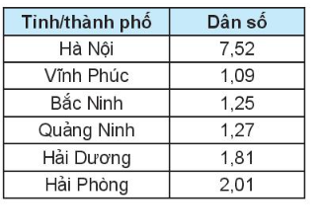
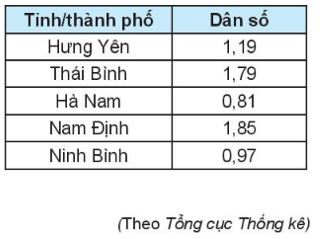
Bài 5.24 trang 90 Toán 10 Tập 1: Bảng sau cho biết dân số của các tỉnh/thành phố Đồng bằng Bắc Bộ năm 2018 (đơn vị triệu người).

Bài 5.23 trang 89 Toán 10 Tập 1: Điểm Toán và Tiếng Anh của 11 học sinh lớp 10 được cho trong bảng sau:

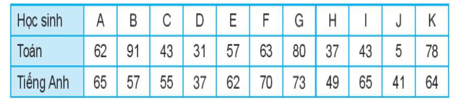
Hãy so sánh mức độ học đều của học sinh môn Tiếng Anh và môn Toán thông qua các số đặc trưng: khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn.

B. Tự luận

Bài 5.22 trang 89 Toán 10 Tập 1: Lương khởi điểm của 5 sinh viên vừa tốt nghiệp tại một trường đại học (đơn vị triệu đồng) là:

3,5     9,2     9,2     9,5     10,5.

a) Giải thích tại sao nên dùng trung vị để thể hiện mức lương khởi điểm của sinh viên tốt nghiệp từ trường đại học này.

b) Nên dùng khoảng biến thiên hay khoảng tứ phân vị để đo độ phân tán? Vì sao?

Bài 5.21 trang 89 Toán 10 Tập 1: Điểm trung bình môn học kì I một số môn học của An là: 8; 9; 7; 6; 5; 7; 3. Nếu An được cộng thêm mỗi môn 0,5 điểm chuyên cần thì các số đặc trưng nào sau đây của mẫu số liệu không thay đổi?

A. Số trung bình.

B. Trung vị.

C. Độ lệch chuẩn.

D. Tứ phân vị.

Bài 5.20 trang 89 Toán 10 Tập 1: Số đặc trưng nào sau đây đo độ phân tán của mẫu số liệu?

A. Số trung bình.

B. Mốt.

C. Trung vị.

D. Độ lệch chuẩn.

Bài 5.19 trang 89 Toán 10 Tập 1: Có 25% giá trị của mẫu số liệu nằm giữa Q1 và Q3, đúng hay sai?

A. Đúng.

B. Sai.

Giải bài tập Toán 10 Bài tập cuối chương 5

A. Trắc nghiệm

Giải Toán 10 trang 89 Tập 1

Bài 5.17 trang 89 Toán 10 Tập 1: Khi cân một bao gạo bằng một cân treo với thang chia 0,2 kg thì độ chính xác d là:

A. 0,1 kg.

B. 0,2kg.

C. 0,3 kg.

D. 0,4kg.

Bài 5.16 trang 88 Toán 10 Tập 1: Tỉ lệ thất nghiệp ở một quốc gia vào năm 2007 (đơn vị %) được cho như sau:

7,8     3,2     7,7     8,7     8,6     8,4     7,2     3,6

5,0     4,4     6,7     7,0     4,5     6,0     5,4.

Hãy tìm các giá trị bất thường (nếu có) của mẫu số liệu trên.

Bài 5.15 trang 88 Toán 10 Tập 1: Mẫu số liệu sau đây cho biết cân nặng của 10 trẻ sơ sinh (đơn vị kg):

2,977          3,155          3,920          3,412          4,236

2,593          3,270          3,813          4,042          3,387.

Hãy tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn cho mẫu số liệu này.

Bài 5.14 trang 88 Toán 10 Tập 1: Từ mẫu số liệu về thuế thuốc lá của 51 thành phố tại một quốc gia, người ta tính được:

Giá trị nhỏ nhất bằng 2,5; Q1 = 36; Q2 = 60; Q3 = 100; giá trị lớn nhất bằng 205.

a) Tỉ lệ thành phố có thuế thuốc lá lớn hơn 36 là bao nhiêu?

b) Chỉ ra hai giá trị sao cho có 50% giá trị của mẫu số liệu nằm giữa hai giá trị này.

c) Tìm khoảng tứ phân vị của mẫu số liệu.

Bài 5.13 trang 88 Toán 10 Tập 1: Cho mẫu số liệu gồm 10 số dương không hoàn toàn giống nhau. Các số đo độ phân tán (khoảng biến thiên, khoảng tứ phân vị, độ lệch chuẩn) sẽ thay đổi như thế nào nếu:

a) Nhân mỗi giá trị của mẫu số liệu với 2.

b) Cộng mỗi giá trị của mẫu số liệu với 2.

Bài 5.12 trang 88 Toán 10 Tập 1: Cho hai biểu đồ chấm điểm biểu diễn hai mẫu số liệu A, B như sau:

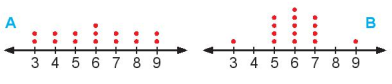
Không tính toán, hãy cho biết:

a) Hai mẫu số liệu này có cùng khoảng biến thiên và số trung bình không?

b) Mẫu số liệu nào có phương sai lớn hơn?

Bài 5.11 trang 88 Toán 10 Tập 1: Mỗi khẳng định sau đúng hay sai?

(1) Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch chuẩn càng lớn.

(2) Khoảng biến thiên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất, bỏ qua thông tin của các giá trị còn lại.

(3) Khoảng tứ phân vị có sử dụng thông tin của giá trị lớn nhất, giá trị bé nhất.

(4) Khoảng tứ phân vị chính là khoảng biến thiên của nửa dưới mẫu số liệu đã sắp xếp.

(5) Các số đo độ phân tán đều không âm.

Luyện tập 4 trang 87 Toán 10 Tập 1: Một mẫu số liệu có tứ phân vị thứ nhất là 56 và tứ phân vị thứ ba là 84. Hãy kiểm tra xem trong hai giá trị 10 và 100 giá trị nào được xem là giá trị bất thường.

Luyện tập 3 trang 87 Toán 10 Tập 1: Dùng đồng hồ đo thời gian có độ chia nhỏ nhất đến 0,001 giây để đo 7 lần thời gian rơi tự do của một vật bắt đầu từ điểm A(VA = 0) đến điểm B. Kết quả đo như sau:

0,398          0,399          0,408          0,410          0,406          0,405          0,402.

(Theo Bài tập Vật lí 10, Nhà xuất bản Giáo dục Việt Nam, 2018)

Hãy tìm phương sai và độ lệch chuẩn cho mẫu số liệu này. Qua các đại lượng này, em có nhận xét gì về độ chính xác của phép đo trên?

Luyện tập 2 trang 86 Toán 10 Tập 1: Mẫu số liệu sau đây cho biết số bài hát ở mỗi album trong bộ sưu tập của An:

12  7  10  9  12  9  10  11  10  14.

Hãy tìm khoảng tứ phân vị cho mẫu số liệu này.

HĐ 2 trang 85 Toán 10 Tập 1: Trong một tuần, nhiệt độ cao nhất trong ngày (đơn vị oC) tại hai thành phố Hà Nội và Điện Biên được cho như sau:

Hà Nội: 23  25  28  28  32  33 35.

Điện Biên: 16  24  26  26  26  27  28.

a) Tính khoảng biến thiên của mỗi mẫu số liệu và so sánh.

b) Em có nhận xét gì về sự ảnh hưởng của giá trị 16 đến khoảng biến thiên của mẫu số liệu về nhiệt độ cao nhất trong ngày tại Điện Biên?

c) Tính các tứ phân vị và hiệu Q3 – Q1 cho mỗi mẫu số liệu. Có thể dùng hiệu này để đo độ phân tán của mẫu số liệu không?

Luyện tập 1 trang 85 Toán 10 Tập 1: Mẫu số liệu sau cho biết chiều cao (đơn vị cm) của các bạn trong tổ:

163  159  172  167  165  168  170  161.

Tính khoảng biến thiên của mẫu số liệu này.

HĐ 1 trang 84 Toán 10 Tập 1: Một cổ động viên đã thống kê điểm số mà hai câu lạc bộ Leicester City và Everton đạt được trong năm mùa giải Ngoại hạng Anh gần đây, từ mùa giải 2014 – 2015 đến mùa giải 2018 – 2019 như sau:

Leicester City: 41   81   44   47   52.

Everton: 47   47   61   49    54.

Cổ động viên cho rằng, Everton thi đấu ổn hơn Leicester City. Em có đồng ý với nhận định này không? Vì sao?

Mở đầu trang 84 Toán 10 Tập 1: Dưới đây là điểm trung bình môn học kì I của hai bạn An và Bình:

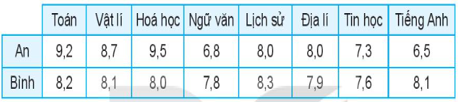
Điểm trung bình môn học kì của An và Bình đều là 8,0 nhưng rõ ràng Bình “học đều” hơn An. Có thể dùng những số đặc trưng nào để đo mức độ “học đều”?

Bài 5.10 trang 83 Toán 10 Tập 1: Bảng sau đây cho biết số chỗ ngồi của một số sân vận động được sử dụng trong Giải Bóng đá Vô địch Quốc gia Việt Nam năm 2018 (số liệu gần đúng).

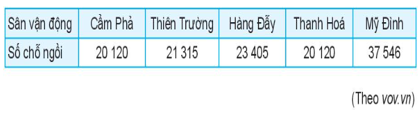
Các giá trị số trung bình, trung vị, mốt bị ảnh hưởng thế nào nếu bỏ đi số liệu chỗ ngồi của Sân vận động Quốc gia Mỹ Đình?

Giải Toán 10 trang 83 Tập 1

Bài 5.9 trang 83 Toán 10 Tập 1: Số học sinh giỏi Quốc gia năm 2018 – 2019 của 10 trường Trung học phổ thông được cho như sau:

0  0  4  0  0  0  10  0  6  0.

a) Tìm số trung bình, mốt, các tứ phân vị của mẫu số liệu trên.

b) Giải thích tại sao tứ phân vị thứ nhất và trung vị trùng nhau.

 Bài 5.8 trang 82 Toán 10 Tập 1: Hãy chọn số đặc trưng đo xu thế trung tâm của mỗi mẫu số liệu sau. Giải thích và tính giá trị của số đặc trưng đó.

a) Số mặt trăng đã biết của các hành tinh:

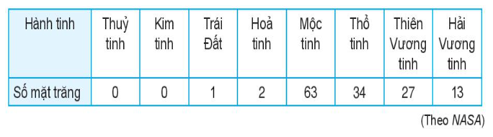
b) Số đường chuyền thành công trong một trận đấu của một số cầu thủ bóng đá:

32   24   20   14   23.

c) Chỉ số IQ của một nhóm học sinh:

80   102   83   103   108   94   110   106   104   100.

d) Các sai số trong một phép đo:

10   15   18   15   14   13   42   15   12   14   42.

Bài tập

Bài 5.7 trang 82 Toán 10 Tập 1: Tìm số trung bình, trung vị, mốt và tứ phân vị của mỗi mẫu số liệu sau đây:

a) Số điểm mà năm vận động viên bóng rổ ghi được trong một trận đấu:

9        8        15      8        20

b) Giá của một số loại giày (đơn vị nghìn đồng):

350    300    650    300    450    500    300    250

c) Số kênh được chiếu của một số hãng truyền hình cáp:

36      38      33      34      32      30      34      35

Giải Toán 10 trang 82 Tập 1

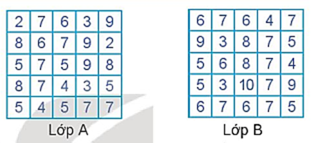
Vận dụng trang 82 Toán 10 Tập 1: Hãy tính các số đặc trưng đo xu thế trung tâm cho mẫu số liệu về điểm khảo sát của lớp A và lớp B ở đầu bài học để phân tích và so sánh hiệu quả học tập của hai phương pháp này.

3. Mốt

HĐ 5 trang 81 Toán 10 Tập 1: Một cửa hàng giày thể thao đã thống kê cỡ giày của một số khách hàng nam được chọn ngẫu nhiên cho kết quả như sau:

38   39   39   38   40   41   39   39   38   39   39   39   40   39   39.

a) Tính cỡ giày trung bình. Số trung bình này có ý nghĩa gì với cửa hàng không?

b) Cửa hàng nên nhập cỡ giày nào với số lượng nhiều nhất?

Giải Toán 10 trang 81 Tập 1

Luyện tập 3 trang 81 Toán 10 Tập 1: Bảng sau đây cho biết số lần học tiếng Anh trên Internet trong một tuần của một số học sinh lớp 10:

Hãy tìm các tứ phân vị cho mẫu số liệu này.

2. Tứ phân vị

Giải Toán 10 trang 80 Tập 1

HĐ 4 trang 80 Toán 10 Tập 1: Điểm (thang điểm 100) của 12 thí sinh cao điểm nhất trong cuộc thi như sau:

58      74      92      81      97      88      75      69      87      69      75      77.

Ban tổ chức muốn trao các giải Nhất, Nhì, Ba, Tư cho các thí sinh này, mỗi giải trao 25% số thí sinh (3 thí sinh).

Em hãy giúp ban tổ chức xác định các ngưỡng điểm để phân loại thí sinh.

Luyện tập 2 trang 79 Toán 10 Tập 1: Chiều dài (đơn vị feet) của 7 con cá voi trưởng thành được cho như sau:

48      53      51      31      53      112    52.

Tìm số trung bình và số trung vị của mẫu số liệu trên. Trong hai số đó, số nào phù hợp hơn để đại diện cho chiều dài của 7 con cá voi trưởng thành này?

HĐ 3 trang 79 Toán 10 Tập 1: Một công ty nhỏ gồm 1 giám đốc và 5 nhân viên, thu nhập hằng tháng của giám đốc là 20 triệu đồng, của mỗi nhân viên là 4 triệu đồng.

a) Tính thu nhập trung bình của các thành viên trong công ty.

b) Thu nhập trung bình có phản ánh đúng thu nhập của nhân viên trong công ty không?

Giải Toán 10 trang 79 Tập 1

Luyện tập 1 trang 79 Toán 10 Tập 1: Bảng sau cho biết thời gian chạy cự li 100 m của các bạn trong lớp (đơn vị giây):

HĐ 2 trang 78 Toán 10 Tập 1: Dựa trên điểm trung bình, hãy cho biết phương pháp học tập nào hiệu quả hơn.

1. Số trung bình và trung vị

Giải Toán 10 trang 78 Tập 1

HĐ 1 trang 78 Toán 10 Tập 1: Tính trung bình cộng điểm khảo sát Tiếng Anh của mỗi lớp A và B.

Giải bài tập Toán 10 Bài 13: Các số đặc trưng đo xu thế trung tâm

Mở đầu

Mở đầu trang 78 Toán 10 Tập 1: Hai phương pháp học Tiếng Anh khác nhau được áp dụng cho hai lớp A và B có trình độ tiếng Anh tương đương nhau. Sau hai tháng, điểm khảo sát tiếng Anh (thang điểm 10) của hai lớp được cho như hình bên.

Quan sát mẫu số liệu trên, có thể đánh giá được phương pháp học tập nào hiệu quả hơn không?

Bài 5.6 trang 77 Toán 10 Tập 1: Làm tròn số 8 316,4 đến hàng chục và 9,754 đến hàng phần trăm rồi tính sai số tuyệt đối của số quy tròn.

 Bài 5.5 trang 77 Toán 10 Tập 1: An và Bình cùng tính chu vi của hình tròn bán kính 2 cm với hai kết quả như sau:

Kết quả của An: S1 = 2πR ≈ 2 . 3,14 . 2 = 12,56 cm;

Bài 5.4 trang 77 Toán 10 Tập 1: Các nhà vật lí sử dụng ba phương pháp đo hằng số Hubble lần lượt cho kết quả như sau:

67,31 ± 0,96;

67,90 ± 0,55;

67,74 ± 0,46.

Phương pháp nào chính xác nhất tính theo sai số tương đối?

Bài 5.3 trang 77 Toán 10 Tập 1: Sử dụng máy tính cầm tay tìm số gần đúng cho $\sqrt[3]{7}$ với độ chính xác 0,0005.