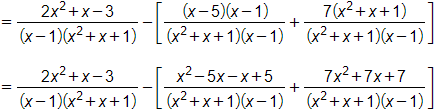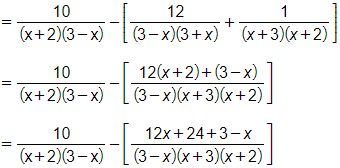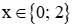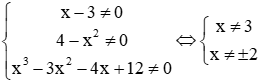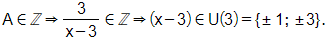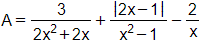30 câu Trắc nghiệm Cộng, trừ phân thức (có đáp án 2024) | Toán 8 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 6: Cộng, trừ phân thức đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 6
Trắc nghiệm Toán 8 Bài 6: Cộng, trừ phân thức
Câu 1. Tìm x, biết : 2x+3+3x2−9=0 (x≠± 3)
A. x = 0
B. x=12
C. x = 1
D. x=32
Đáp án đúng là: D
Ta có 2x+3+3x2−9=2x+3+3(x−3)(x+3)
=2(x−3)(x−3)(x+3)+3(x−3)(x+3)
=2(x−3)+3(x−3)(x+3)=2x−6+3(x−3)(x+3)=2x−3(x−3)(x+3)
Mà 2x+3+3x2−9=0 nên 2x−3(x−3)(x+3)=0
2x−3=0
2x=3
x=32
Vậy x=32.
Câu 2. Rút gọn biểu thức sau: A=2x2+x−3x3−1−x−5x2+x+1−7x−1.
A. A=−6x2+2x−15(x−1)(x2+x+1)
B. A=6x2(x−1)(x2+x+1)
C. A=6x2+15(x−1)(x2+x+1)
D. A=−6x2−15(x−1)(x2+x+1)
Đáp án đúng là: D
A=2x2+x−3x3−1−x−5x2+x+1−7x−1
=2x2+x−3x3−1−(x−5x2+x+1+7x−1)
=2x2+x−3(x−1)(x2+x+1)−x2−5x−x+5+7x2+7x+7(x−1)(x2+x+1)
=2x2+x−3(x−1)(x2+x+1)−8x2+x+12(x−1)(x2+x+1)
=(2x2+x−3)−(8x2+x+12)(x−1)(x2+x+1)
=2x2+x−3−8x2−x−12(x−1)(x2+x+1)=−6x2−15(x−1)(x2+x+1)
Câu 3. Giá trị của biểu thức A=52x+2x−32x−1+4x2+38x2−4xvới x=14 là
A. A=112
B. A=132
C. A=152
D. A=172
Đáp án đúng là: D
A=52x+2x−32x−1+4x2+38x2−4x
=52x+2x−32x−1+4x24x(2x−1)
=5 . 2(2x−1)4x(2x−1)+4x(2x−3)4x(2x−1)+4x2+34x(2x−1)
=20x−104x(2x−1)+8x2−12x4x(2x−1)+4x2+34x(2x−1)
=20x−10+8x2−12x+4x2+34x(2x−1)=12x2+8x−74x(2x−1)
=12x2−6x+14x−74x(2x−1)=6x(2x−1)+7(2x−1)4x(2x−1)
=(6x+7)(2x−1)4x(2x−1)=6x+74x.
Với x=14, ta có:
A=6⋅14+74⋅14=32+71=32+7=32+142=172.
Câu 4. Với x = 2023 hãy tính giá trị của biểu thức: B=1x−23−1x−3.
A. B=12 020
B. B=1202 000
C. B=1200 200
D. B=120 200
Đáp án đúng là: B
B=1x−23−1x−3=x−3(x−23)(x−3)−x−23(x−23)(x−3)
=(x−3)−(x−23)(x−23)(x−3)=x−3−x+23(x−23)(x−3)=20(x−23)(x−3)
Với x = 2023, ta có:
B=20(2023−23)(2023−3)=202000 . 2020
=2020 . 100 . 2020=1100 . 2020=1202 000.
Câu 5. Tính tổng sau: A=11.2+12.3+13.4+...+199.100.
A. A = 1
B. A = 0
C. A=12
D. A=99100
Đáp án đúng là: D
A=11.2+12.3+13.4+...+199.100
=(1−12)+(12−13)+(13−14)+...+(199−1100)
=1−12+12−13+13−14+...+199−1100
=1−1100=99100
Câu 6. Chọn khẳng định đúng.
A. AB−CD=A−CB−D
B. AB−CD=ADBC
C. AB−CD=AD−BCBD
D. AB−CD=A−CBD
Đáp án đúng là: C
Quy đồng mẫu thứcABvà CD, ta có:
AB=ADBD; CD=BCBD.
Do đó AB−CD=ADBD−BCBD=AD−BCBD.
Câu 7. Phân thức đối của phân thức 2x−1x+1 là
A. 2x+1x+1
B. 1−2xx+1
C. x+12x−1
D. x+11−2x
Đáp án đúng là: B
Phân thức đối của phân thức 2x−1x+1 là −2x−1x+1=1−2xx+1.
Câu 8. Thực hiện phép tính sau:x2x+2−4x+2 (x≠−2)
A. x + 2
B. 2x
C. x
D. x – 2
Đáp án đúng là: D
x2x+2−4x+2=x2−4x+2=(x−2)(x+2)x+2
=(x−2)(x+2):(x+2)(x+2):(x+2)=x−21=x−2.
Câu 9. Tìm phân thức A thỏa mãn: x−1x2−2x+A=−x−1x2−2x.
A. 2x−2
B. 22−x
C. 1x
D. 1x+2
Đáp án đúng là: B
x−1x2−2x+A=−x−1x2−2x
Suy ra A=−x−1x2−2x−x−1x2−2x
=−x−1−(x−1)x2−2x=−x−1−x+1x2−2x
=−2xx2−2x=−2xx(x−2)=−2x−2=22−x.
Câu 10. Cho A=2x−16x2−6x−34x2−4. Phân thức thu gọn của A có tử thức là:
A. 4x2−7x−212x(x−1)(x + 1)
B. 4x2−7x+2
C. 4x2−7x−2
D. 12x(x−1)(x + 1)
Đáp án đúng là: C
A=2x−16x2−6x−34x2−4=2x−16x(x−1)−34(x2−1)
=2x−16x(x−1)−34(x−1)(x+1)=2(2x−1)(x+1)−3.3x12x(x−1)(x+1)
=2(2x2−x+2x−1)−9x12x(x−1)(x+1)=2(2x2+x−1)−9x12x(x−1)(x+1)
=4x2+2x−2−9x12x(x−1)(x+1)=4x2−7x−212x(x−1)(x+1).
Câu 11. Cho11−x+11+x+21+x2+41+x4+81+x8=...1−x16. Số thích hợp điền vào chỗ trống là
A. 16
B. 8
C. 4
D. 20
Đáp án đúng là: A
11−x+11+x+21+x2+41+x4+81+x8
=1+x+1−x(1−x)(1+x)+21+x2+41+x4+81+x8
=21−x2+21+x2+41+x4+81+x8
=2(1+x2)+2(1−x2)(1−x2)(1+x2)+41+x4+81+x8
=41−x4+41+x4+81+x8
=4(1+x4)+4(1−x4)(1−x4)(1+x4)+81+x8
=81−x8+81+x8=8(1+x8)+8(1−x8)(1−x8)(1+x8)=161−x16.
Câu 12. Cho 3y – x = 63. Tính giá trị của biểu thức A = xy−2+2x−3yx−6.
A. 1
B. 2
C. 3
D. 4
Đáp án đúng là: D
Ta có 3y – x = 6 nên x = 3y – 63
Thay x = 3y – 6 vàoA = xy−2+2x−3yx−6, ta được:
A=3y−6y−2+2(3y−6)−3y3y−6−6
=3(y−2)y−2+6y−12−3y3y−12
=3+3y−123y−12=3+1=4
Câu 13. Kết luận nào sau đây là đúng khi nói về giá trị của biểu thức A=10(x+2)(3−x)−12(3−x)(3+x)−1(x+3)(x+2) tại x=−34?
A. 0 < A < 1
B. A = 0
C. A = 1
D. A=74
Đáp án đúng là: A
A=10(x+2)(3−x)−12(3−x)(3+x)−1(x+3)(x+2)
=10(x+2)(3−x)−11x+27(3−x)(x+3)(x+2)
=10(x+3)(3−x)(x+2)(x+3)−11x+27(3−x)(x+2)(x+3)
=10(x+3)−(11x+27)(3−x)(x+2)(x+3)=10x+30−11x−27(3−x)(x+2)(x+3)
=−x+3(3−x)(x+2)(x+3)=1(x+2)(x+3)
Tại x=−34ta có A=1(−34+2)(−34+3)=154⋅94=14516=1645
Vậy 0 < A < 1.
Câu 14. Tìm giá trị nguyên của x để biểu thức A = 6x2+ 8x + 7x3−1+xx2+ x + 1−6x−1 có giá trị là một số nguyên.
A. x = 0
B. x = 1
C. x=±1
D.
Đáp án đúng là: D
A = 6x2+ 8x + 7x3−1+xx2+ x + 1−6x−1
=6x2+8x+7(x−1)(x2+x+1)+xx2+x+1−6x−1
=6x2+8x+7+x(x−1)−6(x2+x+1)(x−1)(x2+x+1)
=6x2+8x+7+x2−x−6x2−6x−6(x−1)(x2+x+1)
=x2+x+1(x−1)(x2+x+1)=1x−1
Để A∈ℤhay 1x−1∈ℤ thì x – 1 ∈ Ư(1) = {−1; 1}.
Ta có bảng sau:
|
x – 1 |
−1 |
1 |
|
x |
0 (TM) |
2 (TM) |
Câu 15. Có bao nhiêu giá trị của x để biểu thức A = 3x−3−x24−x2−4x−12x3−3x2−4x + 12 có giá trị là một số nguyên?
A. 1
B. 2
C. 3
D. 4
Đáp án đúng là: C
Điều kiện:
A = 3x−3−x24−x2−4x−12x3−3x2−4x + 12
=3x−3−x24−x2−4x−12x2(x−3)−4(x−3)
=3x−3+x2x2−4−4x−12(x2−4)(x−3)
=3(x2−4)+x2(x−3)−(4x−12)(x−3)(x2−4)
=3x2−12+x3−3x2−4x+12(x−3)(x2−4)
=x3−4x(x−3)(x2−4)=x(x2−4)(x−3)(x2−4)
=xx−3=1+3x−3
Để
Ta có bảng sau:
|
x – 3 |
–3 |
–1 |
1 |
3 |
|
x |
0 (TM) |
2 (KTM) |
4 (TM) |
6 (TM) |
Vậy có 3 giá trị của x để biểu thức A có giá trị là một số nguyên.
Câu 16. Rút gọn biểu thức
biết x>12; x≠1.
A. 12x(x−1)
B. 12x(x+1)
2(x−1)(x+1)
D. 2x(x−1)(x+1)
Đáp án đúng là: A
=32x2+2x+2x−1(x−1)(x+1)−2x
=3(x−1)+2x(2x−1)−4(x−1)(x+1)2x(x−1)(x+1)
=3x−3+4x2−2x−4x2+42x(x−1)(x+1)
=x+12x(x−1)(x+1)=12x(x−1)