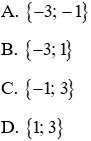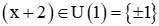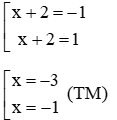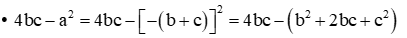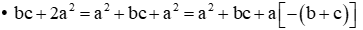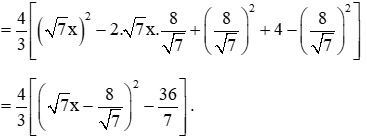30 câu Trắc nghiệm Nhân, chia phân thức (có đáp án 2024) – Toán 8 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 7: Nhân, chia phân thức đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 7
Trắc nghiệm Toán 8 Bài 7: Nhân, chia phân thức
Câu 1. Tìm biểu thức A thỏa mãn biểu thức: x+3y4x+8y . A=x2−9y2x+2y.
A. 4(x – 2y)
B. 4(x + 2y)
C. 4(x + 3y)
D. 4(x – 3y)
Đáp án đúng là: D
x+3y4x+8y . A=x2−9y2x+2y
A=x2−9y2x+2y:x+3y4x+8y
=(x−3y)(x+3y)x+2y:x+3y4(x+2y)
=(x−3y)(x+3y)x+2y⋅4(x+2y)x+3y=4(x−3y).
Câu 2. Tìm mối liên hệ giữa x và y, biết x+yx3+x2y+xy2+y3:x2+xy−2y2x4−y4=2.
A. x = y
B. x = 3y
C. x = – y
D. x = –3y
Đáp án đúng là: D
x+yx3+x2y+xy2+y3:x2+xy−2y2x4−y4
=x+yx2(x+y)+y2(x+y):x2+2xy−xy−2y2(x2−y2)(x2+y2)
=x+y(x2+y2)(x+y):x(x+2y)−y(x+2y)(x−y)(x+y)(x2+y2)
=1(x2+y2):(x−y)(x+2y)(x−y)(x+y)(x2+y2)
=1(x2+y2):x+2y(x+y)(x2+y2)
=1(x2+y2)⋅(x+y)(x2+y2)x+2y=x+yx+2y.
Ta có x+yx3+x2y+xy2+y3:x2+xy−2y2x4−y4=2
x+yx+2y=2
x+y=2x+4y
x=−3y
Câu 3. Tìm x thỏa mãn 3x+15x2−4:x+5x−2=1 (x≠± 2; x≠−5)
A. x = 0
B. x = 1
C. x = – 1
D. x = 3
Đáp án đúng là: B
3x+15x2−4:x+5x−2=3(x+5)(x−2)(x+2):x+5x−2
=3(x+5)(x−2)(x+2)⋅x−2x+5=3x+2
Khi đó 3x+15x2−4:x+5x−2=1
3x+2=1
x+2=3
x=1 (TM)
Câu 4. Cho A=x2+y2+xyx2−y2:x3−y3x2+y2−2xy và B=x2−y2x2+y2:x2−2xy+y2x4−y4.
Khi x + y = 5 hãy so sánh A và B.
A. A = B
B. A≥B
C. A > B
D. A < B
Đáp án đúng là: D
A=x2+y2+xyx2−y2:x3−y3x2+y2−2xy
=x2+y2+xy(x+y)(x−y):(x−y)(x2+y2+xy)(x−y)2
=x2+y2+xy(x+y)(x−y)⋅(x−y)2(x−y)(x2+y2+xy)=1x+y.
Với x + y = 5 ta có A=15
B=x2−y2x2+y2:x2−2xy+y2x4−y4
=(x−y)(x+y)x2+y2:(x−y)2(x2+y2)(x−y)(x+y)
=(x−y)(x+y)x2+y2⋅(x2+y2)(x−y)(x+y)(x−y)2=(x+y)2
Với x + y = 5 ta có B=52=25
Câu 5. Rút gọn biểu thức A=x+1x2+x+1=x3−1x2−1.
A. x2+x+1
B. 1
C. x + 1
D. x – 1
Đáp án đúng là: B
A:x+1x2+x+1=x3−1x2−1
A=x3−1x2−1⋅x+1x2+x+1=(x−1)(x2+x+1)(x−1)(x+1)⋅x+1x2+x+1=1
Câu 6. Phân thức nghịch đảo của phân thức 2x+1x+2 với x≠−12; x≠−2 là
A. 2x+1x+2
B. x+22x+1
C. −x+22x+1
D. −2x+1x+2
Đáp án đúng là: B
Phân thức nghịch đảo của phân thức 2x+1x+2làx+22x+1.
Câu 7. Kết quả phép tính 3x+124x−16⋅8−2xx+4 là
A. 32
B. 32(x−4)
C. −32(x−4)
D. −32
Đáp án đúng là: D
3x+124x−16⋅8−2xx+4=3(x+4)4(x−4)⋅2(4−x)x+4
=3(x+4)4(x−4)⋅−2(x−4)x+4=−32.
Câu 8. Kết quả của phép chia 4x+12(x+4)2:3(x+3)x+4 là
A. 4x+4
B. −4x+4
C. 43(x+4)
D. −43(x+4)
Đáp án đúng là: C
4x+12(x+4)2:3(x+3)x+4=4(x+3)(x+4)2:3(x+3)x+4
=4(x+3)(x+4)2⋅x+43(x+3)=43(x+4).
Câu 9. Kết quả của phép chia x3+1x2+2x+1:3x2−3x+3x2−1 có tử thức gọn nhất là
A. x – 1
B. 3
C. –3
D. x + 1
Đáp án đúng là: A
x3+1x2+2x+1:3x2−3x+3x2−1
=(x+1)(x2−x+1)(x+1)2:3(x2−x+1)(x−1)(x+1)
=(x+1)(x2−x+1)(x+1)2.(x−1)(x+1)3(x2−x+1)
=(x+1)2(x2−x+1)(x−1)3(x+1)2(x2−x+1)=x−13.
Vậy kết quả của phép chia x3+1x2+2x+1:3x2−3x+3x2−1 có tử thức là x − 1.
Câu 10. TínhA=(1−122)(1−132)⋅⋅⋅(1−120102)
A. 20092010
B. 20112010
C. 20114020
D. 20094020
Đáp án đúng là: C
(1−122)(1−132)(1−142)(1−152)⋅⋅⋅(1−1n2)
=22−122⋅32−132⋅42−142⋅52−152⋯n2−1n2
=1. 322⋅2 . 432⋅3 . 542⋅4 . 652⋯(n−1)(n+1)n2
=1.2.3.4...(n−1)2.3.4.5...n.3.4.5.6...(n+1)2.3.4.5...n
=1n.n+12=n+12n
Áp dụng với n = 2010 , ta có:
A=(1−122)(1−132)⋅⋅⋅(1−120102)=2010+12 . 2010=20114020.
Câu 11. Biết x + 3x2−4.8−12x + 6x2−x39x + 27=−AB. Tìm A, B.
A. A = (x−2)2; B = 9(x + 2)
B. A = 9(x + 2); B = (x−2)2
C. A = 9(x−2); B = (x + 2)2
D. A = (x + 2)2; B = 9(x−2)
Đáp án đúng là: A
x + 3x2−4.8−12x + 6x2−x39x + 27
=x + 3(x−2)(x + 2).(2−x)39(x + 3)
=−(x−2)29(x + 2).
Vậy A = (x−2)2; B = 9(x + 2).
Câu 12. Giá trị biểu thức A=52−132−1:92−172−1:132−1112−1:...:552−1532−1là:
A. 928
B. 289
C. 1814
D. 328
A=52−132−1:92−172−1:132−1112−1:...:552−1532−1
=52−132−1⋅72−192−1⋅112−1132−1...532−1552−1
=4.62.4⋅6.88.10⋅10.1212.14...52.5454.56
=62⋅610⋅1014...5256
=3⋅656=928
Đáp án đúng là: A
Câu 13. Tìm giá trị của x để phân thức A chia hết cho phân thức B biết:
A=x3−x2−x+11x−2; B=x+2x−2.
Đáp án đúng là: A
A:B=x3−x2−x+11x−2:x+2x−2=x3−x2−x+11x−2⋅x−2x+2
=x3−x2−x+11x+2=x3+2x2−3x2−6x+5x+10+1x+2
=x2(x+2)−3x(x+2)+5(x+2)+1x+2
=(x+2)(x2−3x+5)+1x+2=x2−3x+5+1x+2.
Để phân thức A chia hết cho phân thức B thì AB∈ℤ.
Suy ra (x2−3x+5+1x+2)∈ℤ
Mà (x2−3x+5)∈ℤ ∀x∈ℤhay
Câu 14. Cho a + b + c = 0. Tính A=4bc−a2bc+2a2⋅4ca−b2ca+2b2⋅4ab−c2ab+2c2.
A. 1
B. 0
C. – 1
D. 2
Đáp án đúng là: A
Do a+b+c=0nên a=−(b+c).
=2bc−b2−c2=−(b−c)2
=a2+bc−ab−ac=(a2−ab)−(ac−bc)
=a(a−b)−c(a−b)=(a−c)(a−b)
Khi đó 4bc−a2bc+2a2=−(b−c)2(a−c)(a−b).
Tương tự, ta có: 4ca−b2ca+2b2=−(c−a)2(b−a)(b−c);
4ab−c2ab+2c2=−(a−b)2(c−a)(c−b)
A=4bc−a2bc+2a2⋅4ca−b2ca+2b2⋅4ab−c2ab+2c2
=−(b−c)2(a−c)(a−b)⋅−(c−a)2(b−a)(b−c)⋅−(a−b)2(c−a)(c−b)=1.
Câu 15. Rút gọn biểu thức sau: A=(1−122)(1−132)...(1−1n2)
A. n+12n
B. n−12n
C. nn−1
D. nn+1
Đáp án đúng là: A
A=(1−122)(1−132)...(1−1n2)
=22−122⋅32−132⋅42−142⋅52−152⋯n2−1n2
=1.322.2.432.3.542.4.652...(n−1)(n+1)n2
=1.2.3.4...(n−1)2.3.4.5...n.3.4.5.6...(n+1)2.3.4.5...n
=1n.n+12=n+12n
Câu 16. Tìm giá trị nhỏ nhất của biểu thức A=(4x2−16).7x−23x+6
A. −367
B. 367
C. −487
D. 487
Đáp án đúng là: C
A=(4x2−16).7x−23x+6=(4x2−16)(7x−2)3x+6
=4(x−2)(x+2)7x−23(x+2)=4(x−2)7x−23
=43(7x2−2x−14x+4)=43(7x2−16x+4)
Ta có: (√7x−8√7)2≥0∀x⇒(√7x−8√7)2−367≥−367∀x
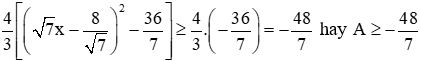
Dấu “=” xảy ra khi và chỉ khi (√7x−8√7)2=0 hay x=87.
Vậy giá trị nhỏ nhất của biểu thức A là−487 khi x=87.