30 câu Trắc nghiệm Hai tam giác đồng dạng (có đáp án 2024) – Toán 8 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 1: Hai tam giác đồng dạng đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 1
Trắc nghiệm Toán 8 Bài 1: Hai tam giác đồng dạng
Câu 1 : Cho ΔABC∽ΔDEF biết ˆA=50o;ˆB=60o . Khi đó số đo góc D bằng
- A
50o .
- B
60o .
- C
70o .
- D
80o .
Đáp án : A
Vì ΔABC∽ΔDEF⇒ˆA=ˆD (hai góc tương ứng)
Mà ˆA=50o(gt)⇒ˆD=50o
Câu 2 : Cho tam giác ABC, trên AB lấy điểm D. Qua D kẻ đường thẳng song song với BC cắt AC ở E. Khẳng định nào sau đâyđúng
- A
ΔABC∽ΔADE .
- B
ΔABC∽ΔAED .
- C
ΔBAC∽ΔADE .
- D
ΔACB∽ΔDEA .
Đáp án : A
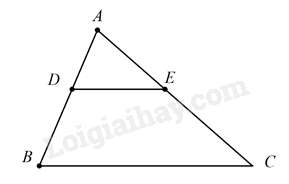
Vì DE//BC⇒ΔABC∽ΔADE(gt)
Câu 3 : Cho ΔABC∽ΔMNP theo tỉ số k1 , ΔMNP∽ΔDEF theo tỉ số k2 . Hỏi ΔABC∽ΔMNP theo tỉ số nào ?
- A
k1 .
- B
k2k1 .
- C
k1k2 .
- D
k1k2 .
Đáp án : C
Vì ΔABC∽ΔDEF theo tỉ số k1⇒ABDE=k1
Vì ΔMNP∽ΔDEF theo tỉ số k2⇒MNDE=k2
⇒ABMN=ABDE:MNDE=k1k2
Câu 4 : Cho ΔABC∽ΔMNP . Biết AB=5cm;BC=6cm;MN=10cm;MP=5cm . Hãy chọn đáp án đúng:
- A
NP=2,5cm;AC=12cm
- B
NP=12cm;AC=2,5cm
- C
NP=5cm;AC=10cm
- D
NP=10cm;AC=5cm
Đáp án : A
Vì ΔABC∽ΔMNP⇒ABMN=ACMP=BCNP (hai cạnh tương ứng)
⇒510=AC5=6NP⇒AC=5.510=2,5cm;NP=10.65=12cm
Câu 5 : Cho ΔABC,ΔMNP biết AB=3cm;AC=4cm;BC=5cm;MN=6cm;MP=8cm;NP=10cm và ˆA=90o;ˆB=60o;ˆM=90o;ˆP=30o thì:
- A
ΔABC∽ΔPNM .
- B
ΔABC∽ΔNMP .
- C
ΔABC∽ΔMNP .
- D
ΔABC∽ΔMPN .
Đáp án : C
ΔABC có ˆC=180o−(ˆA+ˆB)=180o−(90o+80o)=30o (Định lý tổng ba góc trong tam giác )
ΔMNP có ˆN=180o−(ˆM+ˆP)=180o−(90o+30o)=60o (Định lý tổng ba góc trong tam giác)
Xét ΔABC và ΔMNP có:
ABMN=186=3;ACMP=248=3;BCNP=3010=3
⇒ABMN=ACMP=BCNP
Vậy ˆA=ˆM(=90o);ˆB=ˆN(=60o);ˆC=ˆP(=30o)
Câu 6 : Hãy chọn câu đúng.
- A
Hai tam giác bằng nhau thì đồng dạng.
- B
Hai tam giác đồng dạng thì bằng nhau.
- C
Hai tam giác bằng nhau thì không đồng dạng.
- D
Hai tam giác vuông luôn đồng dạng với nhau.
Đáp án : A
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên câu A đúng, câu C sai.
+ Hai tam giác đồng dạng thì chưa chắc bằng nhau nó chỉ bằng nhau khi tỉ số đồng dạng bằng 1 nên câu B sai.
+ Hai tam giác vuông chưa chắc đồng dạng (chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau) nên câu D sai.
Câu 7 : Hãy chọn câu sai.
- A
Hai tam giác bằng nhau thì đồng dạng.
- B
Hai tam giác đều luôn đồng dạng.
- C
Hai tam giác cân thì đồng dạng.
- D
Hai tam giác đồng dạng là hai tam giác có tất cả các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ.
Đáp án : C
+ Hai tam giác bằng nhau có các cặp góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau nên chúng đồng dạng theo tỉ số 1 nên A đúng.
+ Hai tam giác đều có các góc đều bằng 600 và các cạnh của mỗi tam giác bằng nhau nên các cạnh tương ứng tỉ lệ . Vậy hai tam giác đều luôn đồng dạng nên B đúng.
+ Hai tam giác cân chưa đủ điều kiện các cạnh tương ứng tỉ lệ, các góc tương ứng bằng nhau nên không đồng dạng nên C sai
+ Câu D đúng vì là định nghĩa hai tam giác đồng dạng.
Câu 8 : Cho ΔABC,ΔMNP nếu có ˆA=ˆM;ˆB=ˆN;ˆC=ˆP để ΔABC∽ΔMNP theo định nghĩa hai tam giác đồng dạng thì cần bổ sung thêm điều kiện nào?
- A
ABMN=ACMP=BCNP .
- B
ABNP=ACMP=BCNM .
- C
ABMN=ACNP=BCMP .
- D
ABMP=ACNP=BCNM .
Đáp án : A
ΔABC∽ΔMNP⇔{ABMN=ACMP=BCNPˆA=ˆM;ˆB=ˆN;ˆC=ˆP
Mà ˆA=ˆM;ˆB=ˆN;ˆC=ˆP(gt)
nên cần bổ sung thêm điều kiện ABMN=ACMP=BCNP thì ΔABC∽ΔMNP (định nghĩa).
Câu 9 : Cho ΔABC∽ΔMNP theo tỉ số 2. Khẳng định nào sau đây là đúng
- A
MN=2AB .
- B
AC=2NP .
- C
MP=2BC .
- D
BC=2.NP .
Đáp án : D
Vì ΔABC∽ΔMNP theo tỉ số 2 (gt) ⇒BC=2NP
Câu 10 : Hãy chọn câu đúng
Nếu ΔABC∽ΔMNP theo tỉ số k=23 thì ΔMNP∽ΔABC theo tỉ số
- A
23 .
- B
32 .
- C
49 .
- D
43 .
Đáp án : B
Vì ΔABC∽ΔMNP theo tỉ số đồng dạng là k=23 ⇒ΔMNP∽ΔABC theo tỉ số đồng dạng là 1k=32
Câu 11 : ΔABC∽ΔDEF theo tỉ số k=23 , biết ΔABC có chu vi bằng 42cm. Chu vi ΔDEF là:
- A
28cm
- B
2cm
- C
8cm
- D
18cm
Đáp án : A
Vì ΔABC∽ΔDEF theo tỉ số
k=32⇒ABDE=ACDF=BCEF=AB+AC+BCDE+FD+EF=32⇒CVΔABCCVΔEFD=32⇒42CVΔDEF=32⇒CVΔEFD=42.23=28(cm)
Câu 12 : Cho hình vẽ, biết AB // DE. Tính tỉ số độ dài của x và y.
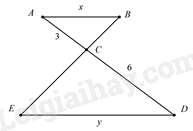
- A
18.
- B
19 .
- C
2.
- D
12 .
Đáp án : D
Vì AB // DE ⇒ΔABC∽ΔDEC (định lí)
⇒ABDE=ACCD (các cạnh tương ứng) ⇒xy=35=12
Câu 13 : Cho ΔABC∽ΔA1B1C1 theo tỉ số 2:3 và ΔA1B1C1∽ΔA2B2C2 theo tỉ số 1 :3. Vậy ΔABC∽ΔA2B2C2 theo tỉ số k bằng
- A
k=3:9
- B
k=2:9
- C
k=2:6
- D
k=1:3
Đáp án : B
Vì ΔABC∽ΔA1B1C1 theo tỉ số 2:3⇒ABA1B1=23
Vì ΔA1B1C1∽ΔA2B2C2 theo tỉ số 1:3⇒A1B1A2B2=13
⇒ABA2B2=ABA1B1.A1B1A2B2=23.13=29
Vậy ΔABC∽ΔA2B2C2 theo tỉ số k=2:9 .
Câu 14 : Cho ΔA1B1C1∽ΔABC theo tỉ số đồng dạng k=23 . Tỉ số chu vi của hai tam giác đó là:
- A
49.
- B
32.
- C
34.
- D
23.
Đáp án : D
Vì ΔA1B1C1∽ΔABC theo tỉ số đồng dạng k=23 .
⇒A1B1AB=A1C1AC=B1C1BC=A1B1+A1C1+B1C1AB+AC+BC=23⇒CVΔA1B1C1CVΔABC=23
Hai tam giác đồng dạng theo tỉ số nào thì chu vi cũng đồng dạng theo tỉ số đó.
Câu 15 : Nếu ΔA1B1C1 đồng dạng với ΔABC theo tỉ số 4 thì tỉ số chu vi của ΔA1B1C1 và ΔABC là
- A
4
- B
16
- C
8
- D
0,25
Đáp án : A
Vì ΔA1B1C1 đồng dạng với ΔABC theo tỉ số 4
⇒A1B1AB=A1C1AC=B1C1BC=A1B1+A1C1+B1C1AB+AC+BC=4⇒CVΔA1B1C1CVΔABC=4
Câu 16 : Cho ΔMNI∽ΔABC theo tỉ số k=57 và hiệu chu vi của 2 tam giác là 16m. Tính chu vi mỗi tam giác.
- A
CΔMNI=30m,CΔABC=46m.
- B
CΔMNI=56m,CΔABC=40m.
- C
CΔMNI=24m,CΔABC=40m.
- D
CΔMNI=40m,CΔABC=56m.
Đáp án : D
Vì ΔMNI∽ΔABC theo tỉ số k=57
⇒MNAB=MIAC=NIBC=MN+MI+NIAB+AC+BC=57⇒CVΔMNICVΔABC=57⇒CVΔMNICVΔABC−CVΔMNI=57−5⇒CVΔMNI16=52⇒CVΔMNI=16.52=40(cm).⇒CVΔABC=40+16=56(cm).
Câu 17 : Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm E sao cho AC = 3.AE. Qua E vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
(I)ΔAME∽ΔADC , tỉ số đồng dạng k1=13
(II)ΔCBA∽ΔADC , tỉ số đồng dạng k2=1
(III)ΔCNE∽ΔADC , tỉ số đồng dạng k3=23
Chọn câu đúng:
- A
(I) đúng, (II) và (III) sai.
- B
(I) và (II) đúng, (III) sai.
- C
(I) , (II), (III) đều đúng.
- D
(I), (II), (III) đều sai.
Đáp án : C
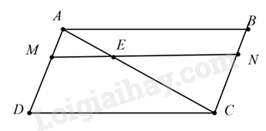
Xét ΔADC có ME//CD (gt) ⇒ΔAME∽ΔADC(1) theo tỉ số đồng dạng k1=AEAC=13
Vì ABCD là hình bình hành nên
+ ⌢B=⌢D
+ AB//CD⇒^BAC=^ACD (so le trong)
+ AD//BC⇒^ACB=^CAD (so le trong)
+ AD = BC ; AB = CD
Xét ΔCBA và ΔADC có :
+ ⌢B=⌢D;^BAC=^ACD;^ACB=^CAD(cmt)
+ ABCD=BCAD=ACAC(=1)
⇒ΔCBA∽ΔADC theo tỉ lệ đồng dạng k2=1
Xét ΔABC có :
EN//CD (gt) mà AB//CD (cmt)
⇒EN//AB⇒ΔCNE∽ΔCBA
Mà ΔCBA∽ΔADC(cmt)
⇒ΔCNE∽ΔADC theo tỉ lệ đồng dạng k3=CEAC=23 (Vì AC=3AE⇒CE=23AC)
Vậy khẳng định (I), (II), (III) đều đúng.
Câu 18 : Cho hình bình hành ABCD.Trên đường chéo AC lấy điểm I sao cho AC=32AI . Qua I vẽ đường thẳng song song với CD cắt AD và BC theo thứ tự ở M và N. Cho các khẳng định sau:
(I)ΔAMI∽ΔADC tỉ số đồng dạng k1=23
(II)ΔCBA∽ΔADC , tỉ số đồng dạng k2=1
(III)ΔCNI∽ΔADC , tỉ số đồng dạng k3=23 .
Số khẳng định đúng là:
- A
1
- B
2
- C
3
- D
4
Đáp án : B
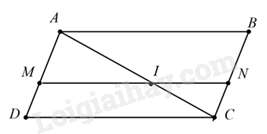
Xét tam giác ADC có MI//CD⇒ΔAMI∽ΔADC(1) theo tỉ số đồng dạng k1=AIAC=23
Vì ABCD là hình bình hành nên:
+ ˆB=ˆD
+ AB//CD⇒^BAC=^ACD (so le trong)
+ AD//BC⇒^ACB=^CAD (so le trong)
+ AD = BC; AB = DC
Xét ΔCBA và ΔADC có :
+ˆB=ˆD;^BAC=^ACD;^ACB=^CAD
+ ABCD=BCAD=ACAC(=1)
⇒ΔCBA∽ΔADC theo tỉ số đồng dạng k2=1
Xét ΔADC có IN // CD (gt) mà AB // CD (cmt)
⇒IN//AB⇒ΔCNI∽ΔCBA
Mà ΔCBA∽ΔADC (cmt)
⇒ΔCNI∽ΔADC theo tỉ số đồng dạng k3=CIAC=13 .
Vậy có 2 khẳng định (I), (II) đúng.
Câu 19 : Cho tam giác ABC , lấy M trên cạnh BC sao cho MBMC=12 Qua M kẻ đường thẳng song song với AC cắt AB tại D và đường thẳng song song với AB cắt AD tại E biết chu vi tam giác MEC bằng 24 cm thì chu vi tam giác DBM là
- A
12cm .
- B
24 cm.
- C
48 cm.
- D
36cm .
Đáp án : A
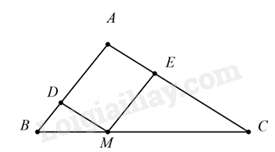
Vì MD // AC ⇒ΔDBM∽ΔABC
Vì ME // AB ⇒ΔEMC∽ΔABC
⇒ΔDBM∽ΔEMC(∽ΔABC)
⇒DBEM=DMEC=BMMC=DB+DM+BMEM+EC+MC=12CVΔDBMCVΔEMC=12
Mà chu vi tam giác MEC bằng 24 cm
Chu vi tam giác DBM bằng 24 : 2 = 12 (cm).
Câu 20 : Cho tam giác ABC , lấy E trên cạnh BC sao cho EBEC=23 Qua E kẻ đường thẳng song song với AC cắt AB tại I và đường thẳng song song với AB cắt AC tại K , biết hiệu chu vi tam giác EKC và chu vi tam giác BEI bằng 24 cm thì chu vi tam giác BEI là
- A
12cm .
- B
24 cm.
- C
48 cm.
- D
36 cm.
Đáp án : C
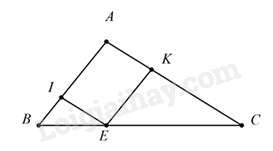
Vì EI // AC ⇒ΔIBE∽ΔABC
Vì EI // AB ⇒ΔKEC∽ΔABC
⇒ΔIBE∽ΔKEC(∽ΔABC)
⇒IBKE=IEKC=BEEC=IB+IE+BEKE+KC+EC=23CVΔIBECVΔKEC=23⇒CVΔIBECVΔKEC−CVΔIBE=23−2⇒CVΔIBE24=21
Chu vi của tam giác IBE bằng 24. 2 = 48 cm