30 câu Trắc nghiệm Hình thang – Hình thang cân (có đáp án 2024) – Toán 8 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 8 (có đáp án) Bài 3: Hình thang – Hình thang cân đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 8 Bài 3
Trắc nghiệm Toán 8 Bài 3: Hình thang – Hình thang cân
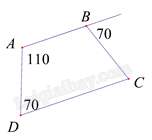
Câu 1 : Cho hình vẽ, số đo ^BCD bằng:
- A
70o
- B
110o
- C
80o
- D
140o
Đáp án : A
Tứ giác ABCD có ˆA+ˆD=110o+70o=180o nên AB // CD suy ra ABCD là hình thang.
Mặt khác ta có: ^ABC=180o−70o=110o
Hình thang ABCD có ˆA=ˆB=110o . Suy ra ABCD là hình thang cân
Suy ra: ˆC=ˆD=70o
Câu 2 : Cho hình thang cân ABCD có AB // CD và AC = 12 cm, AB = 6 cm. Tình BD
- A
12 cm
- B
13 cm
- C
7 cm
- D
6 cm
Đáp án : A
Hình thang cân có hai đường chéo bằng nhau.
Câu 3 : Cho hình thang cân ABCD có AB // CD. Gọi M là giao điểm của AC và BC. Tam giác MCD là tam giác gì:
- A
Tam giác cân
- B
Tam giác nhọn
- C
Tam giác vuông
- D
Tam giác tù
Đáp án : A
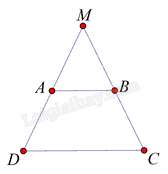
Vì ABCD là hình thang cân có hai đáy là AB và CD nên ˆC=ˆD
Mặt khác xét tam giác MCD có ˆC=ˆD . Suy ra tam giác MCD là tam giác cân.
Câu 4 : Cho hình thang ABCD có AB // CD, hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD. Tìm khẳng định sai trong các khẳng định sau:
- A
ABCD là hình thang cân
- B
AC = BD
- C
BC = AD
- D
Tam giác AOD cân tại C.
Đáp án : D
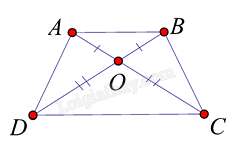
Ta có: OA=OB;OC=OD⇒OA+OC=OB+OD⇒AC=BD
Hình thang ABCD (AB //CD) có AC = BD nên ABCD là hình thang cân
Suy ra: BC = AD
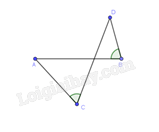
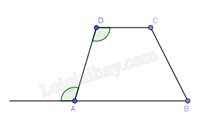
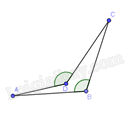
Câu 5 : Trong các tứ giác sau,tứ giác nào là hình thang?
- A
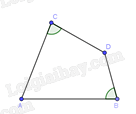 .
. - B
 .
. - C
 .
. - D
 .
.
Đáp án : C
Vậy tứ giác ABCD là hình thang
Câu 6 : Trong các khẳng định sau, khẳng định nào sai?
- A
Tứ giác có hai cạnh bên bằng nhau là hình thang cân.
- B
Hình thang cân có hai cạnh bên bằng nhau.
- C
Hình thang cân có hai góc đối bù nhau.
- D
Hình thang cân có hai góc kề một cạnh đáy bằng nhau.
Đáp án : A
Câu 7 : Hình thang cân là hình thang có
- A
hai góc kề bằng nhau.
- B
hai góc đối bằng nhau.
- C
hai cạnh đối bằng nhau.
- D
hai đường chéo bằng nhau.
Đáp án : D
Câu 8 : Số trục đối xứng của hình thang cân là
- A
0.
- B
1.
- C
2.
- D
3.
Đáp án : B
Câu 9 : Tứ giác ABCD là hình thang vì có
- A
AB // CD.
- B
AB = CD .
- C
AB⊥CD .
- D
AB=CD .
Đáp án : A
Câu 10 : Tứ giác ABCD có AB // CD là một hình thang, ta gọi
- A
các đoạn thẳng AB và CD là các cạnh bên.
- B
các đoạn thẳng AB và CD là các cạnh đáy.
- C
các đoạn thẳng AB và CD là các đường chéo.
- D
các đoạn thẳng AB và CD là các đường cao.
Đáp án : B
Câu 11 : Trong hình thang có hai góc tù:
- A
hai góc còn lại cũng là góc tù.
- B
hai góc còn lại là hai góc vuông.
- C
hai góc còn lại gồm một góc tù và một góc nhọn
- D
hai góc còn lại là hai góc nhọn.
Đáp án : D
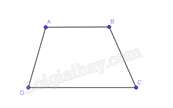
Xét hình thang ABCD có AB // CD nên ˆA+ˆD=180o (2 góc trong cùng phía) suy ra hai góc đó có nhiều nhất một góc nhọn, có nhiều nhất một góc tù.
Tương tự ˆB và ˆC cũng vậy.
Do đó trong bốn góc A, B, C, D có hai góc tù thì hai góc còn lại là hai góc nhọn.
Câu 12 : Cho hình thang ABCD (AB // CD) ta có:
- A
ˆA+ˆD=180o;ˆC+ˆB=180o
- B
ˆA+ˆB=180o;ˆC+ˆD=180o
- C
ˆA+ˆC=180o;ˆB+ˆD=180o
- D
ˆA+ˆB+ˆC+ˆD=180o
Đáp án : A
Hình thang ABCD có AB // CD thì ˆA và ˆD ; ˆB và ˆC là các cặp góc trong cùng phía nên ˆA+ˆD=180o;ˆB+ˆD=180o
Câu 13 : Hình thang cân có một góc bằng 50o . Hiệu giữa hai góc kề một cạnh bên là:
- A
130o
- B
100o
- C
80o
- D
50o
Đáp án : C
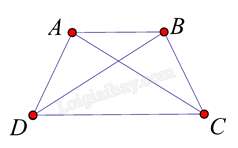
Giả sử ABCD là hình thang có đáy lớn là DC; đáy nhỏ là AB; ˆC=ˆD=50o . Khi đó:
ˆA=ˆB=360o−ˆC−ˆD2=360o−50o−50o2=130o
⇒ˆB−ˆC=ˆA−ˆD=130o−50o=80o
Câu 14 : Cho hình thang ABCD (AB //CD) biết ˆA=58o thì:
- A
ˆD=122o
- B
ˆD=212o
- C
ˆD=22o
- D
ˆD=0o
Đáp án : A
Mà ˆA=58o nên 58o+ˆD=180o⇒ˆD=180o−58o=122o
Câu 15 : Tứ giác nào sau đây không phải hình thang:
- A
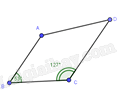 .
. - B
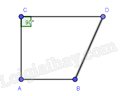 .
. - C
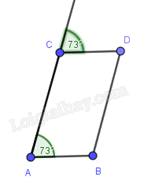 .
. - D
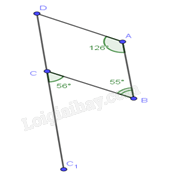 .
.
Đáp án : D
Ta có: ˆA+ˆB=126o+55o=181o nên Bc và AD không song song
Lại có: ˆB≠^BCC1 nên AB và CD không song song với nhau
Vậy tứ giác ABCD ở hình D không phải là hình thang.
Câu 16 : Cho hình vẽ sau. Biết ABCD là hình thang cân (AB // CD).
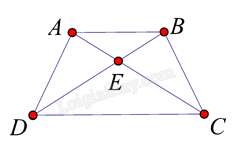
Tìm khẳng định đúng trong các khẳng định sau:
- A
ΔABC=ΔBDA
- B
^CBA=^DBA
- C
ΔABE cân
- D
ΔAED cân
Đáp án : C

Xét tam giác ABC và tam giác BAD có:
AB là cạnh chung
^ABC=^BAC (hai góc kề một đáy của hình thang cân)
BC = AD (hai cạnh bên của hình thang cân)
Suy ra: ΔABC=ΔBAD (c – g – c). Suy ra: ^CAB=^DBA (hai góc tương ứng)
Tam giác ABE có ^EAB=^EBA nên suy ra tam giác ABE là tam giác cân.
Câu 17 : Cho tam giác ABC. Các điểm D và E lần lượt trên các cạnh AB, AC sao cho
DE // BC. Tứ giác DBEC là hình thang cân nếu:
- A
Tam giác ABC vuông tại A.
- B
Tam giác ABC cân tại C.
- C
Tam giác ABC cân tại B.
- D
Tam giác ABC cân tại A.
Đáp án : D
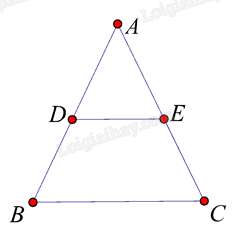
Tứ giác BDEC có DE // BC nên BDEC là hình thang . Để BDEC là hình thang cân thì ˆB=ˆC nên suy ra ABC là tam giác cân tại A.
Câu 18 : Cho tam giác ABC cân tại A. các điểm D và E lần lượt trên các cạnh AB, AC sao cho DE // BC. Tìm khẳng định đúng:
- A
BE = DC
- B
BE = DE
- C
DC = DE
- D
DC = BC
Đáp án : A

Tứ giác DBCE có DE // BC nên DBCE là hình thang
Hình thang DBCE có ˆB=ˆC nên DBCE là hình thang cân
Suy ra: BE = DC
Câu 19 : Cho hình thang cân ABCD (AB // CD) đáy nhỏ AB = 3 cm, đường cao
AH = 5 cm. Biết ˆD=45o . Độ dài đáy lớn CD là:
- A
8cm
- B
11 cm
- C
12 cm
- D
13 cm
Đáp án : D
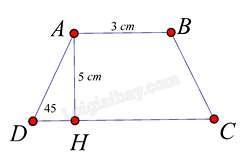
Ta có tam giác AHD vuông cân tại H vì ˆD=45o . Do đó DH = AH = 5 cm
Mà CD = AB + 2DH ⇒CD=3+2.5=13cm
Câu 20 : Cho hình thang cân ABCD có đáy nhỏ AB = 12cm., đáy lớn CD = 22 cm, cạnh bên BC = 13 cm thì đường cao AH bằng:
- A
6 cm
- B
8 cm
- C
9 cm
- D
12 cm
Đáp án : D
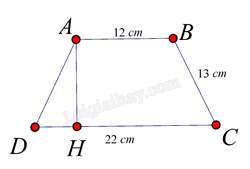
Xét hình thang cân ABCD có đáy lớn CD và đáy nhỏ AB đường cao AH ta có:
CD=AB+2.DH⇒DH=CD−AB2⇒DH=22−122=5cm
Áp dụng định lí Pythago cho tam giác AHD vuông tại H có AD = BC = 13 cm và
DH = 5 cm ta có:
AH2=AD2−DH2=132−52=144⇒AH=√144=12cm
Câu 21 : Cho hình vẽ sau, tính các góc A, C của hình thang ABCD (AB // CD) biết:

- A
ˆA=ˆC=111o
- B
ˆA=ˆC=130o
- C
ˆA=111o;ˆC=130o
- D
ˆA=130o;ˆC=111o
Đáp án : D
Hình thang ABCD có AB // CD nên ˆA=^ADE=130o;ˆC=^ABF=111o
Câu 22 : Hình thang ABCD (AB // CD) có các tia phân giác của ˆA,ˆD cắt nhau tại M thì
- A
^AMD=180o
- B
^AMD=150o
- C
^AMD=90o
- D
^AMD=60o
Đáp án : C
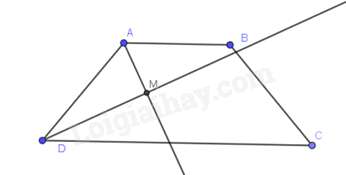
Hình thang ABCD (AB // CD) có các tia phân giác của ˆA,ˆD cắt nhau tại M nên
^DAM+^ADM=12(ˆA+ˆD)=12.180o=90o
Vậy ^AMD=90o
Câu 23 : Hình thang ABCD (AB // CD) biết ˆA−ˆD=40o,ˆB=3ˆC . Các góc của hình thang là:
- A
ˆA=70o;ˆB=135o;ˆC=45o;ˆD=110o
- B
ˆA=110o;ˆB=135o;ˆC=45o;ˆD=70o
- C
ˆA=70o;ˆB=45o;ˆC=135o;ˆD=110o
- D
ˆA=135o;ˆB=70o;ˆC=45o;ˆD=110o
Đáp án : B
Hình thang ABCD (AB // CD) có ˆA+ˆD=180o mà ˆA−ˆD=40o
⇒ˆA=220o:2=110o
Do đó: ˆD=180o−110o=70o
Lại có: ˆB+ˆC=180o (2 góc trong cùng phía) mà ˆB=3ˆC nên
4ˆC=180o⇒ˆC=180o:4=45o
Suy ra: ˆB=3ˆC=3.45o=135o
Câu 24 : Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC vẽ tam giác BCD vuông cân tại B. Tứ giác ABCD có:
- A
^ACD=30o
- B
^ACD=45o
- C
^ACD=60o
- D
^ACD=90o
Đáp án : D
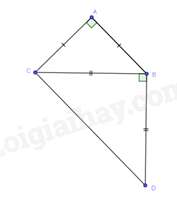
Xét tam giác BCD vuông cân tại B có ^BCD=^BDC=45o (2)
Từ (10, (2) suy ra: ^ACB+^BCD=90o=^ACD
Câu 25 : Cho hình thang cân ABCD (AB // CD). Giả sử AB≤CD . Tìm khẳng định đúng:
- A
BD2−BC2=CD.AB
- B
BD2−BC2=AB2
- C
BD2−BC2=2CD.AB
- D
BD2−BC2=BC.AB
Đáp án : A
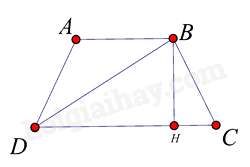
Kẻ BH⊥CD tại H.
Xét tam giác vuông BDH, theo định lý Pytago ta có: BD2=DH2+BH2
Xét tam giác vuông CBH, theo định lý Pytago ta có: BC2=CH2+BH2
Suy ra: BD2−BC2=DH2−CH2=(DH+CH)(DH−CH)=CD.AB
DH + CH = CD; DH – CH = AB