30 câu Trắc nghiệm Hình tam giác đều. Hình vuông. Hình lục giác đều (có đáp án 2024) – Toán 6 Kết nối tri thức

Trắc nghiệm Toán lớp 6 Bài 18: Hình tam giác đều. Hình vuông. Hình lục giác đều

Phần 1. Trắc nghiệm Hình tam giác đều. Hình vuông. Hình lục giác đều

I. Nhận biết

Câu 1. Hình lục giác đều có bao nhiêu đường chéo?

A. 1

B. 2

C. 3

D. 6

Lời giải Hình lục giác đều có tất cả ba đường chéo.

Đáp án: C

Câu 2. Trong các hình vẽ dưới đây, Có bao nhiêu hình là hình lục giác đều?

A. 1

B. 2

C. 3

D. 4

Lời giải

Hình 1) là hình các viên gạch lục giác đều.

Hình 2) là hộp mứt tết cổ truyền có dạng hình lục giác đều.

Hình 3) là tổ ong có dạng hình lục giác đều.

Hình 4) là khay đựng bánh kẹo có dạng hình lục giác đều.

Vậy cả 4 hình đều là hình lục giác đều.

Đáp án: D

Câu 3. Quan sát các hình dưới đây và cho biết hình nào là hình vuông, hình nào là hình tam giác đều, hình nào là hình lục giác đều?

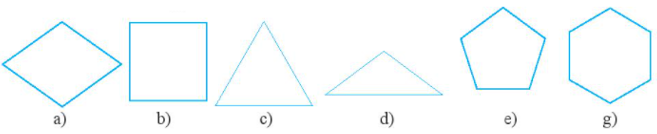
A. Hình vuông là b), tam giác đều là d), lục giác đều là e).

B. Hình vuông là a), tam giác đều là c), lục giác đều là g).

C. Hình vuông là a), tam giác đều là d), lục giác đều là e).

D. Hình vuông là b), tam giác đều là c), lục giác đều là g).

Lời giải

Quan sát hình vẽ và tiến hành đo ta thấy:

- Hình vuông: b;

- Hình tam giác đều: c;

- Hình lục giác đều: g.

Đáp án: D

Câu 4. Hình nào có số cạnh ít nhất trong các hình sau:

A. Hình tam giác đều

B. Hình vuông

C. Hình lục giác đều

D. Cả ba hình có số cạnh bằng nhau.

Lời giải

- Số cạnh của tam giác đều là 3;

- Số cạnh của hình vuông là: 4;

- Số cạnh của hình lục giác đều là: 6;

Đáp án: A

Câu 5. Phát biểu nào dưới đây là sai?

A. Hình vuông có hai đường chéo vuông góc với nhau.

B. Hình lục giác đều có sáu góc bằng nhau.

C. Hình tam giác đều có ba đường chéo bằng nhau.

D. Hình vuông có bốn góc bằng nhau bằng 900.

Lời giải Hình tam giác đều không có đường chéo nên phát biểu C là sai.

Đáp án: C

Câu 6. Hình nào dưới đây là hình biểu diễn tam giác đều?

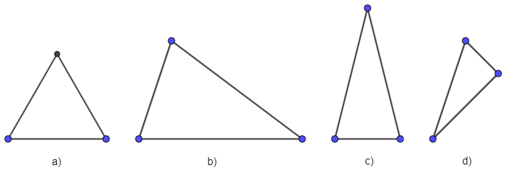
A. Hình a)

B. Hình b)

C. Hình c)

D. Hình d)

Lời giải Trong các hình trên: Hình a) là hình biểu diễn tam giác đều.

Đáp án: A

Câu 7. Cho phát biểu sau: “……….. là hình có ba cạnh bằng nhau và ba góc bằng nhau bằng 600. Điền từ thích hợp vào chỗ trống.

A. Hình vuông

B. Hình lục giác đều

C. Hình tam giác đều

D. Cả A, B và C đều sai.

Lời giải Tam giác đều là hình có ba cạnh bằng nhau và ba góc bằng nhau bằng 600.

Đáp án: C

Câu 8. Cho các biển báo giao thông dưới đây:

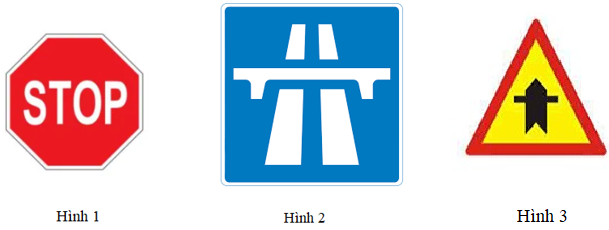
Phát biểu nào dưới đây là đúng?

A. Hình 1 là biển báo dừng lại có hình lục giác đều.

B. Hình 2 là biển báo chỉ đường có hình vuông.

C. Hình 3 là biển báo đường giao nhau có hình tam giác đều.

D. Cả A, B và C đều đúng.

Lời giải

Hình 1 là biển báo dừng lại có hình lục giác đều. Do đó A đúng.

Hình 2 là biển báo chỉ đường có hình vuông. Do đó B đúng.

Hìn 3 là biển báo đường giao nhau có hình tam giác đều. Do đó C đúng.

Vậy cả A, B và C đều đúng.

Đáp án: D

Câu 9. Có bao nhiêu tính chất dưới đây là của hình vuông?

i) Hình vuông có bốn cạnh bằng nhau.

ii) Hình vuông có bốn góc bằng nhau và bằng 600.

iii) Hình vuông có hai đường chéo bằng nhau.

A. 0   

B. 1

C. 2

D. 3

Lời giải

Trong hình vuông:

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng 900.

- Hai đường chéo bằng nhau.

Suy ra i) và iii) là tính chất của hình vuông. 

Vậy có 2 tính chất thỏa mãn của hình vuông.

Đáp án: C

Câu 10. Hình lục giác đều là hình:

A. Có 6 cạnh.

B. Có 5 cạnh bằng nhau.

C. Có 4 cạnh bằng nhau.

D. Có 6 cạnh bằng nhau.

Lời giải Hình lục giác đều là hình có 6 cạnh bằng nhau.

Đáp án: D

II. Thông hiểu 

Câu 1. Phát biểu nào dưới đây là sai?

A. Nếu tam giác MNP có MN = NP thì tam giác MNP là tam giác đều.

B. Nếu tam giác MNP có góc M bằng góc N bằng góc P bằng 600 thì tam giác MNP là tam giác đều.

C. Nếu tam giác MNP có MN = NP = PQ thì tam giác MNP đều.

D. Nếu tam giác MNP có NP = PQ thì chưa chắc tam giác MNP đã là tam giác đều.

Lời giải

Nếu tam giác MNP có ba cạnh MN = NP = PQ thì tam giác MNP đều hoặc nếu tam giác MNP có ba góc M, góc N, góc P đều bằng 600 thì tam giác MNP đều.  Do đó B, C đúng.

Còn nếu tam giác MNP chỉ có hai cạnh bằng nhau thì chưa chắc là tam giác đều. Do đó D đúng và A sai.

Đáp án: A

Câu 2. Nối cột A với cột B để được các bước vẽ hình vuông 7cm một cách chính xác:

Cột A		Cột B
1) Bước 1		a) Vẽ đường thẳng đi qua B vuông góc với AB. Trên đường thẳng này lấy điểm C sao cho BC bằng 7cm.
2) Bước 2		b) Nối điểm B với điểm C lại ta được hình vuông ABCD cạnh 7cm.
3) Bước 3		c) Vẽ cạnh AB bằng 7cm
4) Bước 4		d) Vẽ đường thẳng đi qua A vuông góc với AB. Trên đường thẳng này lấy điểm D sao cho AD bằng 7cm

A. 1 – c; 2 – a; 3 – d; 4 – b.

B. 1 – c; 2 – b; 3 – d; 4 – a.

C. 3 – d; 4 – a; 1 – c; 2 – b.

D. 4 – a; 3 – d; 1- c; 2 – b.

Lời giải

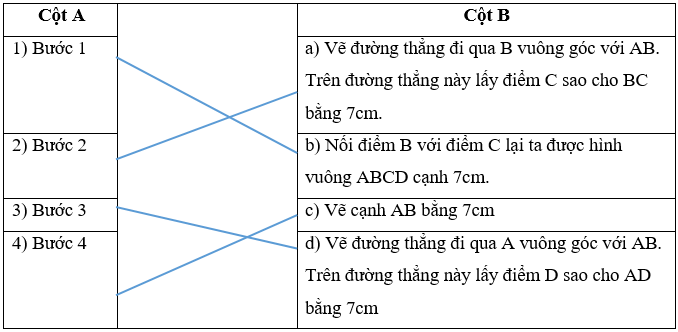
Vậy 1 – c; 2 – a; 3 – d; 4 – b. 

Chú ý: Giữa hai bước 3 và bước 4 có thể thức hiện bước nào trước cũng được.

Đáp án: A

Câu 3. Hình lục giác đều có đường chéo chính dài 18 cm. Số đo cạnh của hình lục giác đều là:

A. 18cm

B. 6cm

C. 12cm

D. 9cm

Lời giải

Do hình lục giác được ghép từ 6 tam giác đều như sau:

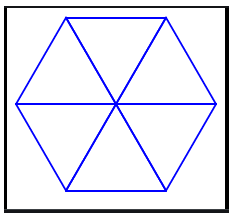
Do đó cạnh tam giác đều bằng: 18:2 = 9cm.

Mà cạnh của tam giác đều cũng chính là cạnh của hình lục giác đều.

Vậy số đo cạnh của hình lục giác đều có đường chéo chính dài 18cm là: 9cm.

Đáp án: D

Câu 4. Sắp xếp các bước vẽ hình tam giác đều cạnh 2cm: 

1) Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 2cm.

2) Vẽ đoạn thẳng AB bằng 2cm.

3) Nối các điểm A với C, B với C ta được tam giác đều ABC cạnh 2 cm.

4) Hai đường tròn tâm A và tâm B cắt nhau tại điểm C. 

A. 1 – 3 – 2 – 4 

B. 1 – 2 – 4 – 3 

C. 2 – 3 – 1 – 4 

D. 2 – 1 – 4 – 3 

Lời giải

Các bước để vẽ tam giác đều như sau: 

2) Vẽ đoạn thẳng AB bằng 2cm.

1) Vẽ đường tròn tâm A bán kính 2cm và đường tròn tâm B bán kính 2cm.

4) Hai đường tròn tâm A và tâm B cắt nhau tại điểm C. 

3) Nối các điểm A với C, B với C ta được tam giác đều ABC cạnh 2 cm.

Đáp án: D

Câu 5. Trong hình dưới đây có bao nhiêu hình vuông?

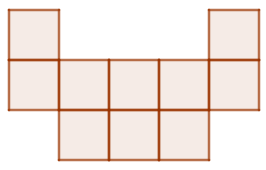
A. 10

B. 11

C. 12

D. 13

Lời giải

Có 10 hình vuông nhỏ

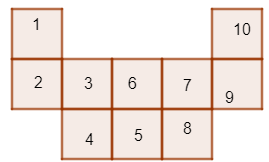
Và hai hình vuông vừa:

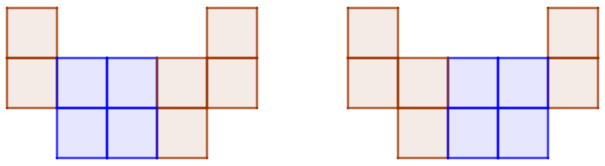
Vậy tổng cộng có 12 hình vuông.

Đáp án: C

Câu 6. Hình lục giác đều được ghép từ:

A. 5 hình tam giác đều.

B. 3 tam giác đều.

C. 6 tam giác đều.

D. 4 tam giác đều.

Lời giải

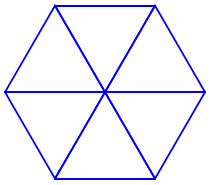
Ta thấy hình lục giác đều được ghép từ 6 tam giác đều.

Đáp án: C

Phần 2. Lý thuyết Hình tam giác đều, hình vuông, hình lục giác đều

1. Hình tam giác đều

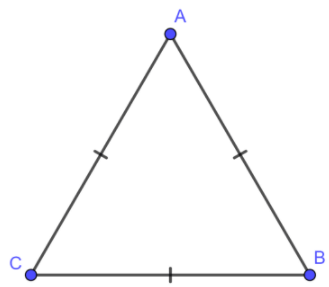
Trong tam giác đều:

- Ba cạnh bằng nhau.

- Ba góc bằng nhau và bằng 600C.

Ví dụ 1. Trong các hình dưới đây, hình nào là tam giác đều:

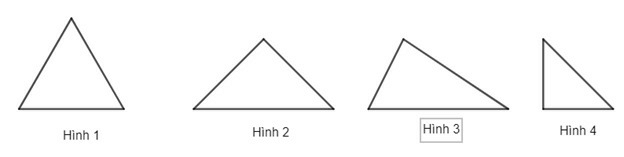
Lời giải

Sử dụng thước thẳng đo lần lượt các cạnh của từng hình, ta nhận thấy:

Hình 1 có độ dài các cạnh bằng nhau. Do đó HÌnh 1 là tam giác đều.

2. Hình vuông

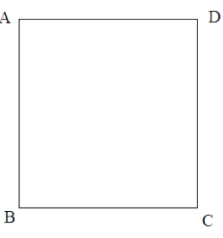
Trong hình vuông:

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng 900.

- Hai đường chéo bằng nhau.

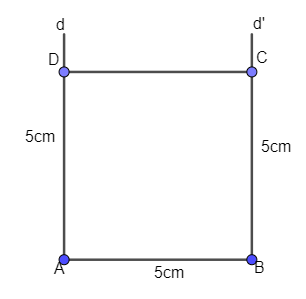
Ví dụ 2. Vẽ hình vuông ABCD có cạnh bằng 5cm.

Lời giải

Bước 1. Vẽ đoạn thẳng AB = 5cm;

Bước 2. Qua A dựng đường thẳng d vuông góc với AB, qua B dựng đường thẳng d’ vuông góc với AB.

Bước 3. Trên đường thẳng d lấy điểm D sao cho AD = 5cm, trên d’ lấy điểm C sao cho BC = 5cm.

Bước 4. Nối D với C ta được hình vuông ABCD.

3. Hình lục giác đều

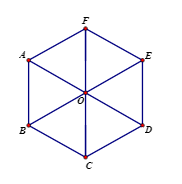
Hình lục giác đều có:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau, mỗi góc bằng 1200.

- Ba đường chéo chính bằng nhau.

Ví dụ 3. Hãy quan sát hình vẽ:

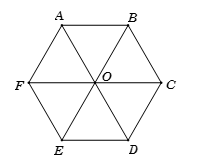
a) Hãy kể tên các đường chéo chính của hình lục giác đều ABCDEF.

b) Hãy so sánh độ dài các đường chéo chính với nhau.

Lời giải

a) Các đường chéo chính của hình lục giác đều ABCDEF là: AD, BE, CF.

b) Sau khi đo độ dài ta thấy AD = BE = CF = 2,1 cm.