30 câu Trắc nghiệm Phép nhân hai số nguyên (có đáp án 2024) – Toán 6 Kết nối tri thức

Trắc nghiệm Toán lớp 6 Bài 16: Phép nhân hai số nguyên

Phần 1. Trắc nghiệm Phép nhân hai số nguyên

I. Nhận biết

Câu 1. Tích của các số nguyên âm có số thừa số là số chẵn thì:

A. là số lẻ

B. là số chẵn

C. là số dương

D. là số âm

Lời giải Tích của các số nguyên âm có số thừa số là số chẵn thì có dấu dương.

Đáp án: C

Câu 2. Cho tích 213.3 = 639. Từ đó suy ra nhanh kết quả của các tích sau: (- 213).3; 

A. -639

B. 639

C. 1 278

D. -1 278

Lời giải

Ta có: 213.3 = 639

Từ đó suy ra: 

(- 213).3 = - 639

Đáp án: A

Câu 3. Tích của một số nguyên a bất kì với số 0 có kết quả là:

A. a

B. 1

C. 0

D. a2

Lời giải Ta có: a.0 = 0

Đáp án: C

Câu 4. Tích của các số nguyên âm có số thừa số là số lẻ thì:

A. là số lẻ

B. là số chẵn

C. là số dương

D. là số âm

Lời giải Tích của các số nguyên âm có số thừa số là số lẻ thì mang dấu âm.

Đáp án: D

Câu 5. Tích của hai số nguyên âm là số thế nào?

A. là số nguyên âm

B. là số nguyên dương

C. là số 0

D. vừa là số nguyên âm vừa là số nguyên dương

Lời giải

Sau bài này ta sẽ biết được là:

Tích của hai số nguyên âm sẽ là một số nguyên dương.

Đáp án: B

Câu 6. Thực hiện phép tính sau: (-5).4

A. – 20

B. 20

C. 10

D. -10 

Lời giải (-5).4 = -(5.4) = - 20

Đáp án: A

Câu 7. Phép nhân có tính chất gì:

A. Tính chất giao hoán

B. Tính chất kết hợp

C. Tính chất phân phối của phép nhân với phép cộng

D. Cả ba tính chất trên

Lời giải Phép nhân có cả ba tính chất: giao hoán, kết hợp và phân phối của phép nhân với phép cộng.

Đáp án: D

II. Thông hiểu

Câu 1. Không thực hiện phép tính, hãy so sánh: (+4).(-8) với 0; 

A. (+4).(-8) ≥ 0  

B. (+4).(-8) > 0

C. (+4).(-8) = 0

D. (+4).(-8) < 0

Lời giải Vì (+4).(- 8) ra kết quả mang dấu âm. Do đó (+4).(- 8) < 0.

Đáp án: D

Câu 2. Thực hiện phép tính: (- 3).(- 2).(- 5). 4;                                             

A. 150

B. 120

C. -120

D. -150

Lời giải (- 3).(- 2) .(- 5) .4 = [(-3).4)].[(-2).(-5)] = (-12).10 =  -120.

Đáp án: C

Câu 3. Một kho lạnh đang ở nhiệt độ , một công nhân cần đặt chế độ làm cho nhiệt độ của kho trung bình cứ mỗi phút giảm đi. Hỏi sau 5 phút nữa nhiệt độ trong kho là bao nhiêu?

A. 20C

B. 100C

C. – 100C

D. – 20C

Lời giải

Cứ mỗi phút giảm 

Sau 5 phút nhiệt độ giảm: 5.2 = 100C

Vậy: Sau 5 phút nữa nhiệt độ trong kho là: 8 – 10 = -20C.

Đáp án: D

Câu 4. Tính giá trị của biểu thức trong mỗi trường hợp sau: 19x với x = - 7;

A. 124

B. -124

C. 133

D. - 133

Lời giải

Thay x = -7 vào 19x, ta được:

19.(-7) = -133.

Vậy với x = -7 thì giá trị biểu thức là -133.

Đáp án: D

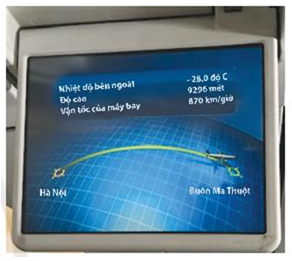
Câu 5. Bạn Hồng đang ngồi trên máy bay, bạn ấy thấy màn hình thông bảo nhiệt độ bên ngoài máy bay là . Máy bay đang hạ cánh, nhiệt độ bên ngoài trung bình mỗi phút tăng lên . Hỏi sau 10 phút nữa nhiệt độ bên ngoài máy bay là bao nhiêu độ C? 

A. 40C

B. 400C

C. 220C

D. 120C

Lời giải

Nhiệt độ bên ngoài trung bình mỗi phút tăng lên 40C.

Sau 10 phút nữa nhiệt độ tăng: 4.10 = 400C.

Vậy: Sau 10 phút nữa nhiệt độ bên ngoài máy bay là:  - 28 + 40 = 120C.

Đáp án: D

Câu 6. Một xí nghiệp may gia công có chế độ thưởng và phạt như sau: Một sản phẩm tốt được thưởng 50 000 đồng, một sản phẩm có lỗi bị phạt 40 000 đồng. Chị Mai làm được 20 sản phẩm tốt và 4 sản phẩm bị lỗi. Chị Mai nhận được bao nhiêu tiền?

A. 84 000 đồng

B. 1 000 000 đồng

C. -160 000 đồng

D. 840 000 đồng

Lời giải

Chị Mai nhận được số tiền là: 

20. (+50 000) + 4. (-40 000) = 1 000 000 + (- 160 000) = 840 000 (đồng)

Vậy chị Mai nhận được 840 000 đồng.

Đáp án: D

Câu 7. Tính tổng hai tích sau: a = (-2).(-3) và c = (+3).(+2);      

A. a + c = 6

B. a + c = 12

C. a + c = -12

D. a + c = -6          

Lời giải

a = (-2).(-3) = 2.3 = 6;

c = (+3).(+2) = 3.2 = 6;

suy ra a + c = 6 + 6 = 12

Đáp án: B

Câu 8. P là tích của 8 số nguyên khác 0 trong đó có đúng 4 số dương. Q là tích của 6 số nguyên khác 0 trong đó có duy nhất một số dương. Hãy cho biết P và Q là số dương hay số âm. 

A. P dương, Q âm

B. P âm, Q dương

C. P, Q đều âm

D. P, Q đều dương

Lời giải

P là tích của 8 số nguyên khác 0 và có đúng 4 số dương nên 4 số còn lại nguyên âm. 

Mà tích của 4 số nguyên dương là một số nguyên dương, tích của 4 số nguyên âm còn lại cùng là một số nguyên dương. Do đó P dương.

Q là tích của 6 số nguyên khác 0 trong đó có duy nhất một số dương nên 5 số còn lại là số nguyên âm và tích của 5 số nguyên âm cũng là một số nguyên âm. Do đó Q âm.

Đáp án: A

Câu 9. Thực hiện phép tính: (-2).29 + (-2).(-99) + (-2).(-30).

A. 199

B. 299

C. 200

D. -199

Lời giải

(-2).29 + (-2).(-99) + (-2).(-30).

= (-2).[29 + (-99) + (-30)]         

= (-2).[(-70) + (-30)]

= (-2).(-100)

= 2 . 100

= 200.

Đáp án: C

Câu 10. Tính:  (-8).(-6)(-125);  

A. 480

B. - 4 800

C. - 6 000    

D. -1 200

Lời giải (-8).(-6)(-125) = [(-8).(-125)].(-6) = 1 000.(-6) = -6 000;

Đáp án: C

III. Vận dụng

Câu 1. Báo cáo kinh doanh trong 6 tháng đầu năm của công ty Bình An được thống kê như sau:

Tháng	Lợi nhuận (triệu đồng)
Tháng 1	50
Tháng 2	-10
Tháng 3	50
Tháng 4	40
Tháng 5	-20
Tháng 6	-10

Sau 6 tháng đầu năm, công ty Bình An kinh doanh lãi hay lỗ với số tiền là bao nhiêu?

A. 50 (triệu đồng)

B. 100 (triệu đồng)

C. 150 (triệu đồng)

D. -50 (triệu đồng)

Lời giải

Số tiền của công ty Bình An thu được sau 6 tháng đầu năm là:

50 + (-10) + 50 + 40 + (-20) + (-10) = 100 (triệu đồng)

Vậy sau 6 tháng đầu năm, công tu Bình An kinh doanh lãi 100 triệu đồng.

Đáp án: B

Câu 2. So sánh hai biểu thức sau:

P = (8 765 – 5 678).[5 678 – 9 765 + (-12)] và Q = 4 342.

A. P > Q

B. P < Q

C. P = Q

D. P ≤ Q

Lời giải

Ta có 8 765 – 5 678 > 0, 5 678 – 9 765 + (-12) < 0.

Do đó (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 0 mà 4 342 > 0.

Vậy (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 4 342 hay P < Q.

Đáp án: B

Câu 3. Cho hai số nguyên x, y (x ≠ 0, y ≠ 0, x > y, x ≠ -y).

Gọi m = x2.y2.(x – y).(x + y)4. Khẳng định nào sau đây đúng về giá trị của m?

A. m là số nguyên âm

B. m là số nguyên dương

C. m = 0

D. m là một số nguyên âm nhỏ hơn -1.

Lời giải

Vì x > y nên x – y > 0.

Ta có x2 ≥ 0 với mọi x mà x ≠ 0 nên x2 > 0.

Ta có y2 ≥ 0 với mọi x mà y ≠ 0 nên y2 > 0.

Ta lại có x ≠ - y nên x + y ≠ 0 suy ra (x + y)4 > 0.

Do đó m = x2.y2.(x – y).(x + y)4 > 0.

Vậy m là một số nguyên dương.

Đáp án: B

Câu 4. Tìm số nguyên x thỏa mãn: (x – 6).(x – 3) = 0;                         

A. x = 6

B. x = 3

C. x = -6, x = -3

D. x = 6, x = 3            

Lời giải

(x – 6).(x – 3) = 0

TH1: x – 6 = 0

x = 6.

TH2: x – 3 = 0

x = 3

Vậy x = 6 hoặc x = 3.               

Đáp án: D

Câu 5. Thực hiện phép tính: (-8).(-8).(-8).(-8) – 84 + 105.

A. 2.84

B. 84 + 10

C. 0

D. 105

Lời giải

(-8).(-8).(-8).(-8) – 84 + 105

= 84 – 84 + 105

= 0 + 105

= 105.

Đáp án: D

Câu 6. Tính giá trị của biểu thức trong trường hợp sau:

(- 2021)abc + ab với a = -21, b = -11 và c = 0.

A. 0

B. 231

C. – 2021

D. 221

Lời giải

Thay a = -21, b = -11 và c = 0 vào biểu thức (- 2021)abc + ab, ta được:

(- 2021)(-21).(-11).0 + (-21).(-11)

= 0 + 231

= 231.

Vậy với a = -21, b = -11 và c = 0 thì giá trị biểu thức là 231.

Đáp án: B

Câu 7. Tính một cách hợp lí: 121.(-63) + 63.(-53) – 63.26.

A. -12 000

B. 12 000

C. 12 600

D. – 12 600

Lời giải

121.(-63) + 63.(-53) – 63.26

= 121.(-63) + (-63).53 + (-63).26

= (-63).(121 + 53 + 26)

= (-63).200

= -12 600.

Đáp án: D

Phần 2. Lý thuyết Phép nhân số nguyên

1. Nhân hai số nguyên khác dấu

Quy tắc nhân hai số nguyên khác dấu

Muốn nhân hai số nguyên khác dấu, ta nhân phần số tự nhiên của hai số đó với nhau rồi đặt dấu “-” trước kết quả nhận được.

Nếu m, n ∈ N* thì m.(-n) = (-n).m = - (m.n).

Ví dụ 1. Thực hiện phép nhân sau:

a) (-23).12;                     b) 134.(-25);                            c) 6.(-32).

Lời giải

a) (-23).12 = - (23.12) = -276;

b) 134.(-25) = - (134.25) = - 3350;

c) 6.(-32) = - (6.32) = -192.

2. Nhân hai số nguyên cùng dấu

Quy tắc nhân hai số nguyên âm 

Muốn nhân hai số nguyên âm, ta nhân phần số tự nhiên của hai số đó với nhau.

Nếu m, n ∈ N*  thì (-m).(-n) = (-n).(-m) = m.n.

Ví dụ 2. Thực hiện các phép nhân sau:

a) (-12).(-32);                           b) (-138).(-25);                         c) (-10).(-5 134).

Lời giải

a) (-12).(-32) = 12.32 = 384;

b) (-138).(-25) = 138.25 = 3450;

c) (-10).(-5 134) = 10. 5 134 = 51 340.

3. Tính chất của phép nhân

Phép nhân các số nguyên có các tính chất:

Giao hoán: a.b = b.a;

Kết hợp: (a.b).c = a.(b.c);

Phân phối của phép nhân đối với phép cộng: a.(b + c) = a.b + a.c.

Ví dụ 3. Tính một cách hợp lí:

a) (125).(-134).(-8);

b) 12.(-27) + 12.(-73);

c) 4.(1 930 + 2 019) + 4.(-2 019).

Lời giải

a) (125).(-134).(-8)

= [125.(-8)].(-134)

= (-1000).(-134)

= 134 000.

b) 12.(-27) + 12.(-73)

= 12.[(-27) + (-73)]

= 12. (-100)

= - 1 200.

c) 4.(1 930 + 2 019) + 4.(-2 019)

= 4.1 930 + 4.2 019 + 4.(-2 019)

= 4.1 930 + [4.2 019 + 4.(-2 019)]

= 4.1 930 + 4.[2019 + (-2 019)]

= 4.1 930 + 4.0

= 7 720.