30 câu Trắc nghiệm Tính toán với số thập phân (có đáp án 2024) – Toán 6 Kết nối tri thức

Trắc nghiệm Toán lớp 6 Bài 29: Tính toán với số thập phân

Phần 1. Trắc nghiệm Tính toán với số thập phân

Câu 1. Thực hiện các phép tính sau: 0,15.4,4 ta được kết quả là:

A. 6,6

B. 0,66

C. 6,60

D. 0,066

Trả lời:

0,15.4,4 = 0,66

Đáp án cần chọn là: B

Câu 2. Thực hiện phép tính: (−4,5) + 3,6 + 4,5 + (−3,6) ta được kết quả là:

A. 0

B. 1

C. 2

D. 3

Trả lời:

(−4,5) + 3,6 + 4,5 + (−3,6) = [(−4,5) + 4,5] + [3,6 + (−3.6)] = 0 + 0 = 0

Đáp án cần chọn là: A

Câu 3. Thực hiện các phép tính sau: (−45,5).0,4 ta được kết quả là:

A. 18,2

B. −18,2

C. −182

D. −1,82

Trả lời:

 (−45,5).0,4 = −(45,5.0,4) = −18,2

Đáp án cần chọn là: B

Câu 4. Thực hiện các phép tính sau: −0,18.(−1,5) ta được kết quả là:

A. −0,27

B. −2,7

C. 0,27

D. 2,7

Trả lời:

−0,18.(−1,5) = 0,18.1,5 = 0,27

Đáp án cần chọn là: C

Câu 5. Tính diện tích S của một hình tròn có bán kính R = 10cm theo công thức 

S = πR2 với π = 3,142

A. 31,4cm2

B. 314cm2

C. 64,8cm2

D. 314cm2

Trả lời:

Diện tích hình tròn là: S = 3,14.102 = 314cm2

Đáp án cần chọn là: B

Câu 6.

Điền số thích hợp vào chỗ trống

Thực hiện phép tính: 3,176 − (2,104 + 1,18) ta được kết quả là: ….

Trả lời:

3,176 − (2,104 + 1,18) = 3,176 − 3,284 = −0,108

Câu 7. Điền vào chỗ trống:

Diện tích một hình chữ nhật có chiều dài 31,21 cm và chiều rộng 22,52 cm là

…. cm2

Trả lời:

Diện tích của hình chữ nhật đó là:

31,21.22,52 = 702,8492(cm2)

Câu 8.

 Khối lượng vitamin C trung bình trong một quả ớt chuông là 0,135 g, còn trong một quả cam là 0,045 g. Khối lượng vitamin C trong quả ớt chuông gấp bao nhiêu lần trong quả cam?

A. 2 lần

B. 3 lần

C. 4 lần

D. 5 lần

Trả lời:

Khối lượng vitamin C trong quả ớt chuông gấp số lần trong quả cam là:

0,135 : 0,045 = 3 ( lần)

Đáp số: 3 lần.

Đáp án cần chọn là: B

Câu 9. Tính chu vi của một hình tròn có bán kính R = 1,25 m theo công thức

C = 2πR với π = 3,14.

A. 7,855 m2

B. 7,855 m

C. 7,585 m2

D. 7,558 m2

Trả lời:

Chu vi của hình tròn đó là:

C = 2πR = 2.3,142.1,25 = 7,855 (m2)

Đáp số: 7,855 m2

Đáp án cần chọn là: A

Câu 10. Điền số thích hợp vào ô trống

Thực hiện phép tính sau: 12,3 + 5,67 ta được kết quả là …..

Hiển thị đáp án

Trả lời:

12,3 + 5,67 = 17,97

Câu 11. Điền số thích hợp vào ô trống

Kết quả của phép tính ( −12,3) + (−5,67) là …..

Trả lời:

 (−12,3) + (−5,67) = −17,97   

Câu 12. Điền số thích hợp vào ô trống

Thực hiện phép tính −5,5 + 90,67 ta được kết quả là:…

Trả lời:

−5,5 + 90,67 = 90,67 − 5,5 = 85,17

Câu 13. Điền số thích hợp vào ô trống

Kết quả của phép trừ 0,008 − 3,9999 là :…..

Trả lời:

0,008 − 3,9999 = 0,008 + (−3,9999) = −(3,9999 − 0,008) = −3,9919

Câu 14. Điền số thích hợp vào ô trống

Cho biết một quả chuối nặng 100 g có chứa:

- Chất béo: 0,3 g

- Kali: 0,42 g.

Trong quả chuối đó, khối lượng kali nhiều hơn khối lượng chất béo là : ……

Trả lời:

Khối lượng kali nhiều hơn khối lượng chất béo là: 

0,42 − 0,3 = 0,12(g)

Câu 15. Tính một cách hợp lí: 89,45 + (−3,28) + 0,55 + (−6,72) ta được kết quả bằng

A. 80

B. −80

C. 100

D. −100

Trả lời:

89,45 + (−3,28) + 0,55 + (−6,72)

= 89,45 + 0,55 + (−3,28) + (−6,72)

= (89,45+0,55) + [(−3,28) + (−6,72)]

 = 90 + (−10) = 90 – 10 = 80

Đáp án cần chọn là: A

Câu 16. Bạn Nam cao 1,57 m, bạn Linh cao 1,53 m, bạn Loan cao 1,49 m.

Trong ba bạn đó, bạn nào cao nhất? Bạn nào thấp nhất?

A. Bạn Nam cao nhất, bạn Loan thấp nhất

B. Bạn Linh cao nhất, bạn Loan thấp nhất

C. Bạn Nam cao nhất, bạn Linh thấp nhất

D. Bạn Loan cao nhất, bạn Nam thấp nhất

Trả lời:

Ta thấy: 1,57 > 1,53 > 1,49

=> Bạn Nam cao nhất, bạn Loan thấp nhất.

Đáp án cần chọn là: A

Câu 17. Nam cao 1,57 m, bạn Linh cao 1,53 m, bạn Loan cao 1,49 m. hiểu

Chiều cao của bạn cao nhất hơn bạn thấp nhất là bao nhiêu mét?

A. 0,18m

B. 0,08m

C. 0,04m

D. 0,14m

Trả lời:

Chiều cao của bạn cao nhất hơn bạn thấp nhất là: 1,57 - 1,49 = 0,08 (m)

Đáp án cần chọn là: B

Câu 18. Bác Đồng của ba thanh gỗ: thanh thứ nhất dài 1,85 m, thanh thứ hai dài hơn thanh thứ nhất 10 cm. Độ dài thanh gỗ thứ ba ngắn hơn tổng độ dài hai thanh gỗ đầu tiên là 1,35 m. Thanh gỗ thứ ba mà bác Đồng đã cưa dài bao nhiêu mét?

A. 1,95m

B. 3,8m

C. 2,48m

D. 2,38m

Trả lời:

Đổi 10cm = 0,1m

Chiều dài thanh gỗ thứ hai là: 1,85 + 0,1 = 1,95 (m)

Tổng chiều dài hai thanh gỗ đầu tiên là: 1,85 + 1,95 = 3,8(m)

Chiều dài thanh gỗ thứ ba là: 3,8 − 1,35 = 2,48 (m)

Đáp án cần chọn là: C

Câu 19.  Tính chu vi của hình tam giác sau:

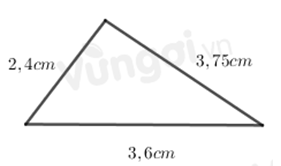
A. 7,85(cm)

B. 7,95(cm2)

C. 7,55(cm2)

D. 7,95(cm)

Trả lời:

Chu vi hình tam giác là: 

2,4 + 3,75 + 3,6 = 7,95 (cm).

Đáp án cần chọn là: D

Phần 2. Lý Thuyết Tính toán với số thập phân

1. Phép cộng, trừ số thập phân

– Muốn cộng hai số thập phân âm, ta cộng hai số đối của của chúng và đặt dấu trừ đằng trước.

(–a) + (–b) = – (a + b) với a, b > 0

– Muốn cộng hai số thập phân khác dấu ta làm như sau: 

+ Nếu 0 < a b thì (–a) + b = b – a

+ Nếu a > b > 0 thì (–a) + b = –(a – b)

– Tương tự với phép cộng của số nguyên và phép cộng của phân số, phép cộng hai số thập phân cũng có các tính chất giao hoán, tính chất kết hợp, tính chất cộng với số 0.

Cho a, b, c là ba số thập phân khi đó ta có: 

Tính chất giao hoán: a + b = b + a

Tính chất kết hợp: (a + b) + c = a + (b + c)

Tính chất cộng với số 0: a + 0 = 0 + a = a.

– Phép trừ hai số thập phân được đưa về phép cộng hai số đối:

a – b  = a + (–b)

Ví dụ 1: 

a) 3, 17 + (–1, 12) =  3, 17 – 1, 12 = 2, 05

Trình bày theo cách đặt tính

 

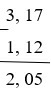
b) 4, 06 – 5, 13 = 4, 06 + (–5, 13) = –(5, 13 – 4, 06) = –1, 07

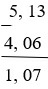
2. Phép nhân số thập phân

Ta thực hiện phép nhân hai số thập phân theo quy tắc tương tự như phép nhân hai số nguyên.

– Nhân hai số cùng dấu: (–a).(–b) = a.b  với a, b > 0

– Nhân hai số khác dấu: (–a).b = a.(–b) = – (a.b) với a, b > 0

– Tương tự với phép nhân số nguyên và phép nhân phân số, phép nhân các số thập phân cũng có các tính chất giao hoán, tính chất kết hợp, tính chất nhân với 1, tính chất phân phối của phép cộng và phép nhân.

Cho ba số thập phân a, b, c ta có: 

– Tính chất giao hoán: a.b = b.a

– Tính chất kết hợp: (a.b).c = a.(b.c)

– Tính chất nhân với số 1: a.1 = 1. a = a

– Tính chất phân phối giữa phép cộng và phép nhân: (a + b).c = a.c + b.c

Ví dụ 2: 

(–2, 14) . (–3, 12) = 2, 14 . 3, 12 = 6, 6768

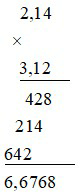
3. Phép chia số thập phân

Ta thực hiện phép chia hai số thập phân theo quy tắc tương tự như phép chia hai số nguyên.

– Chia hai số nguyên cùng dấu:

(–a) : (–b) = a : b với a, b > 0

– Chia hai số nguyên khác dấu:

(–a) : b = a : (–b) = –(a:b) với a, b > 0

Ví dụ 3: 

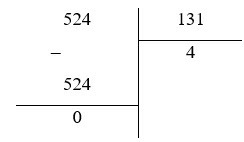
a) (–5, 24) : 1, 31 = –(5, 24 : 1, 31) = –(524 : 131) = –4

b) 24, 25 : (–0, 625) = –(24, 250 : 0, 625) = –(24 250 : 625) = –38,8

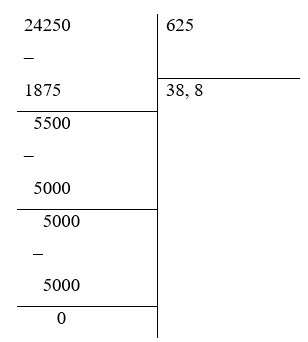
4. Tính giá trị biểu thức với số thập phân

Phép cộng và phép nhân số thập phân cũng có các tính chất giao hoán, kết hợp, phân phối như phép cộng, phép nhân số nguyên và phân số. Vận dụng các tính chất này và quy tắc dấu ngoặc, ta có thể tính giá trị biểu thức một cách hợp lí.

Ví dụ 4: 

a) 12, 53 + 3, 47 – 2, 53 + 6, 53

= (12, 53 – 2, 53) + (3, 47 + 6, 53)

= 10 + 10 = 20

b) 35, 17 . 64, 25 + 35, 17 . 35, 75 – 2, 14 . 100

= 35, 17. (64, 25 + 35, 75) – 2, 14 . 100

= 35, 17. 100 – 2, 14 . 100

= 100 . (35, 17 – 2, 14) 

= 100 . 33, 03 = 3303