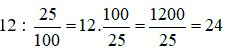30 câu Trắc nghiệm Một số bài toán về tỉ số và tỉ số phần trăm (có đáp án 2024) – Toán 6 Kết nối tri thức
Bộ 30 câu hỏi trắc nghiệm Toán 6 (có đáp án) Bài 31: Một số bài toán về tỉ số và tỉ số phần trăm đầy đủ các mức độ sách Kết nối tri thức giúp học sinh ôn luyện trắc nghiệm Toán 6 Bài 31.
Trắc nghiệm Toán lớp 6 Bài 31: Một số bài toán về tỉ số và tỉ số phần trăm
Phần 1. Trắc nghiệm Một số bài toán về tỉ số và tỉ số phần trăm
Dạng 1.Một số bài toán về tỉ số và tỉ số phần trăm
Câu 1. Tỉ số giữa học sinh nam và học sinh nữ là 80%. Tìm số học sinh nam, biết lớp 6A có 36 học sinh?
A. 20 học sinh.
B. 17 học sinh.
C. 19 học sinh.
D. 16 học sinh.
Trả lời:
Đổi 80%=45, tức là số học sinh nam bằng 45 số học sinh nữ.
Tổng số phần là: 4 + 5 = 9 (phần)
Lớp 6A có số học sinh nam là:
36 : 9.4 = 16 (học sinh)
Vậy lớp có 16 học sinh nam.
Đáp án cần chọn là: D
Câu 2. Hiệu của hai số là 21. Biết 37,5% số lớn bằng 0,6 số nhỏ. Hai số đó là
A. 56; 35
B. 45; 56
C. 60; 39
D. 56; 45
Trả lời:
Đổi 37,5%=38;0,6=35
Tỉ số giữa số lớn và số nhỏ là: 35:38=85
Hiệu số phần bằng nhau là:
8 – 5 = 3 (phần)
Số lớn là: 21:3 × 8 = 56
Số nhỏ là: 56 – 21 = 35
Vậy hai số đó là 56; 35
Đáp án cần chọn là:
Câu 3. Chọn câu sai. Viết dưới dạng tỉ số của hai số tự nhiên.
A.21112618=1021
B.6623%=1125
C.0,72:2,7=415
D.0,075:5%=32
Trả lời:
Đáp án A: 21112618=21112:618=3512:498=3512.849=1021 nên A đúng.
Đáp án B: 6623%=2003:100=2003.1100=23 nên B sai.
Đáp án C: 0,72:2,7=72100:2710=1825.1027=415 nên C đúng
Đáp án D: 0,075:5%=751000:5100=751000.1005=32 nên D đúng.
Đáp án cần chọn là: B
Câu 4. Tìm một số biết 35% của nó bằng 00,3.
A. 100
B. 60
C. 30
D. 50
Trả lời:
Đổi 35%=35:100=3500
Số đó là: 0,3:3500=310.5003=50
Vậy số cần tìm là 50
Đáp án cần chọn là: D
Câu 5. Sắp xếp theo thứ tự tăng dần 23%;12100;−1112;−3124;512 ta được:
A.−3124<−1112<12100<512<23%
B.−3124<−1112<23%<12100<512
C.−3124<−1112<12100<23%<512
D.−1112<−3124<12100<23%<512
Trả lời:
Ta có:23%=23100;−1112=−1312;512=112
Ta chia thành hai nhóm phân số là: 23100;12100;112 và −1312;−3124
Nhóm 1: 12100<23100<1<112 nên 12100<23100<112
Nhóm 2: −1312;−3124
−1312=−2624>−3124 nên −1312>−3124
Vậy −3124<−1312<12100<23100<112 hay −3124<−1112<12100<23%<512
Đáp án cần chọn là: C
Câu 6. Tìm x biết (1,16−x).5,25(1059−714).2217=75%
A. 0
B. 65
C. 425
D. 1
Trả lời:
(1,16−x).5,25(1059−714).2217=75%(116100−x).525100(959−294).3617=75100(2925−x).21411936.3617=34(2925−x).2147=34(2925−x).214.4=7.3(2925−x).21=212925−x=21:212925−x=1x=2925−1=425
Đáp án cần chọn là: C
Câu 7. Tìm y biết 2y + 30%y = −2,3
A. 1
B. 2
C. −1
D. −2
Trả lời:
2y+30%y=−2,32y+310y=−23102310y=−2310y=−2310:2310=-1
Đáp án cần chọn là: C
Dạng 2.Các dạng toán về tỉ số và tỉ số phần trăm
Câu 1. Tỉ số và tỉ số phần trăm của số 2700m và 6km lần lượt là
A.920;45%
B.920;4,5%
C.450;45000%
D.9200;4,5%
Trả lời:
Đổi 6000m
+ Tỉ số của 2700m và 6000m là 2700:6000 = 920
+ Tỉ số phần trăm của 2700m so với 6000m là 2700.1006000%=45%
Đáp án cần chọn là: A
Câu 2. Minh đọc quyển sách trong 4 ngày. Ngày thứ nhất Minh đọc được 25 số trang sách. Ngày thứ hai Minh đọc được 35 số trang sách còn lại. Ngày thứ ba đọc được 80% số trang sách còn lại sau ngày thứ hai và ngày thứ tư đọc 30 trang cuối cùng. Hỏi cuốn sách đó có bao nhiêu trang?
A. 375 trang
B. 625 trang
C. 500 trang
D. 650 trang
Trả lời:
Số phần trang sách còn lại sau ngày thứ nhất là: 1−25=35 (quyển sách)
Số phần trang sách đọc được của ngày thứ hai là: 35.35=925 (quyển sách)
Số phần trang sách còn lại sau ngày thứ hai là: 1−25−925=625 (quyển sách)
Số phần trang sách đọc được ngày thứ ba là: 625.80%=24125 (quyển sách)
Số phần trang sách ứng với 30 trang cuối của ngày thứ tư là:
1−25−925−24125=6125 (quyển sách)
Số trang sách của quyển sách là: 30:6125=625 (trang sách)
Vậy quyển sách có 625 trang
Đáp án cần chọn là: B
Câu 3. Một lớp có chưa đến 50 học sinh. Cuối năm có 30% số học sinh xếp loại giỏi; 38 số học sinh xếp loại khá, còn lại là trung bình. Tính số học sinh trung bình.
A. 15 học sinh
B. 13 học sinh
C. 20 học sinh
D. 9 học sinh
Trả lời:
Đổi 30%=310
Vì số học sinh phải là số tự nhiên nên phải chia hết cho 10 và 8
BCNN(10,8) = 40 nên số học sinh của lớp là 40
Phân số chỉ số học sinh trung bình là: 1−310=38=1340 (số học sinh)
Số học sinh trung bình là: 40.1340=13 (học sinh)
Vậy lớp có 13 học sinh trung bình.
Đáp án cần chọn là: B
Câu 4. Tỉ số của hai số aa và bb là 120%. Hiệu của hai số đó là 16. Tìm tổng hai số đó.
A. 96
B. 167
C. 150
D. 176
Trả lời:
Đổi 120%=120100=65
Hiệu số phần bằng nhau là:
6 – 5 = 1 (phần)
Số lớn là: 16:1.6 = 96
Số bé là: 16:1.5 = 80
Tổng hai số là: 96 + 80 = 176
Đáp án cần chọn là: D
Câu 5. Trong một khu vườn có trồng ba loại cây mít, hồng và táo. Số cây táo chiếm 30% tổng số cây, số cây hồng chiếm 50% tổng số cây, số cây mít là 40 cây. Hỏi tổng số cây trong vườn là bao nhiêu?
A. 20 cây
B. 200 cây
C. 100 cây
D. 240 cây
Trả lời:
40 cây mít ứng với:
100% − 30% − 50% = 20% (tổng số cây)
Tổng số cây trong vườn là: 40:20%=40:20100=200 (cây)
Vậy có 200 cây trong vườn.
Đáp án cần chọn là: B
Câu 6. Một cửa hàng bán một tấm vải trong 4 ngày. Ngày thứ nhất bán 16 tấm vải và 5m; ngày thứ hai bán 20% số còn lại và 10m; ngày thứ ba bán 25% số còn lại và 9m; ngày thứ tư bán 13 số vải còn lại. Cuối cùng, tấm vải còn lại 13m.13m. Tính chiều dài tấm vải ban đầu.
A. 87m
B. 78m
C. 60
D. 38
Trả lời:
Số mét vải của ngày thứ tư khi chưa bán là: 13:(1−13)=392(m)
Số mét vải của ngày thứ ba khi chưa bán là: (392+9):(1−25%)=38(m)
Số mét vải của ngày thứ hai khi chưa bán là: (38+10):(1−20%)=60(m)
Số mét vải của ngày đầu tiên khi chưa bán là: (60+5):(1−16)=78(m)
Vậy lúc đầu tấm vải dài số mét là: 78m.
Đáp án cần chọn là: B
Phần 2. Lý thuyết Một số bài toán về tỉ số và tỉ số phần trăm
1. Tỉ số và tỉ số phần trăm
– Tỉ số của số a và số b là thương của phép chia a cho b, được viết là a : b (với b khác 0)
Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số hai số đo cùng hai đại lượng đó.
Ví dụ 1:
Tỉ số của 3 và 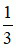 là 3 :
là 3 : 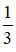
Tỉ số của 1 dm và 1 m là 1 : 10 vì ta phải đổi về cùng đơn vị do đó ta đổi 1 m = 10 dm.
– Trong thực hành, ta thường dùng tỉ số dưới dạng tỉ số phần trăm.
– Tỉ số phần trăm của hai số a và b là 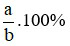
2. Hai bài toán về tỉ số phần trăm
Bài 1: Tìm giá trị phần trăm của một số cho trước.
Muốn tìm m % của một số a đã cho ta tính a .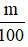
Ví dụ 2: 75% của 48 là 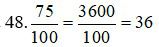
Bài 2: Tìm một số biết giá trị phần trăm của số đó:
Muốn tìm một số khi biết m % của số đó bằng b ta tính b :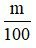
Ví dụ 3: 25 % của một số là 6 thì số đó là 6 : 25 % =