Lý thuyết Các quy tắc tính đạo hàm (Chân trời sáng tạo 2024) Toán 11

Lý thuyết Toán 11 Bài 2: Các quy tắc tính đạo hàm - Chân trời sáng tạo

A. Lý thuyết Các quy tắc tính đạo hàm

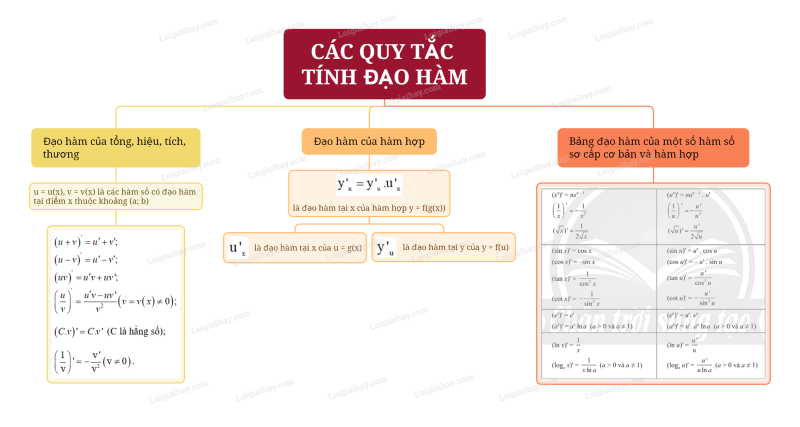
1. Đạo hàm của tổng, hiệu, tích, thương

Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc tập xác định. Khi đó

$\begin{array}{l}{\left(u+v\right)}^{\mathrm{\prime }}=u^{\prime }+v^{\prime };\\ {\left(u-v\right)}^{\mathrm{\prime }}=u^{\prime }-v^{\prime };\\ {\left(uv\right)}^{\mathrm{\prime }}=u^{\prime }v+u{v}^{\prime };\\ {\left(\frac{u}{v}\right)}^{\mathrm{\prime }}=\frac{u^{\prime }v-u{v}^{\prime }}{v^2}\left(v=v\left(x\right)\ne 0\right);\end{array}$

${\left(C.v\right)}^{\prime }=C.v^{\prime }$ (C là hằng số);

${\left(\frac{1}{v}\right)}^{\prime }=-\frac{v^{\prime }}{v^2}\left(v\ne 0\right)$.

2. Đạo hàm của hàm hợp

Nếu hàm số u = g(x) có đạo hàm tại x là $u{}_x^{\prime }$ và hàm số y = f(u) có đạo hàm tại y là $y{}_u^{\prime }$ thì hàm hợp y = f(g(x)) có đạo hàm tại x là $y{}_x^{\prime }=y{}_u^{\prime }.u{}_x^{\prime }$.

3. Bảng đạo hàm của một số hàm số sơ cấp cơ bản và hàm hợp

4. Đạo hàm cấp hai

Cho hàm số y = f(x) có đạo hàm tại mọi điểm $x\in \left(a;b\right)$ thì ta có hàm số $y^{\prime }=f^{\prime }\left(x\right)$ xác định trên (a; b).

Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) tại x, kí hiệu là y” hoặc f”(x).

$f^{″}\left(x\right)={\left(f^{\prime }\left(x\right)\right)}^{\prime }$.

Ý nghĩa cơ học của đạo hàm cấp hai

Đạo hàm cấp hai f”(t) là gia tốc tức thời tại thời điểm t của vân chuyển động có phương trình $s=f\left(t\right)$.

Sơ đồ tư duy Các quy tắc tính đạo hàm

B. Bài tập Các quy tắc tính đạo hàm

Đang cập nhật ...