Lý thuyết Hàm số mũ. Hàm số lôgarit (Chân trời sáng tạo 2024) Toán 11

Lý thuyết Toán 11 Bài 3: Hàm số mũ. Hàm số lôgarit - Chân trời sáng tạo

A. Lý thuyết Hàm số mũ. Hàm số lôgarit

1. Hàm số mũ

- Hàm số $y=a^x\left(a>0,a\ne 1\right)$ được gọi là hàm số mũ cơ số a.

- Hàm số $y=a^x\left(a>0,a\ne 1\right)$ có:

+ Tập xác định: $D=\mathbb{R}$.

+ Tập giá trị: $T=\left(0;+\mathrm{\infty }\right)$.

+ Hàm số liên tục trên $\mathbb{R}$.

+ Sự biến thiên:

• Nếu a > 1 thì hàm số đồng biến trên $\mathbb{R}$ và $\underset{x\to +\mathrm{\infty }}{lim}y=+\mathrm{\infty };\underset{x\to -\mathrm{\infty }}{lim}y=0$.
• Nếu 0 < a < 1 thì hàm số nghịch biến trên $\mathbb{R}$ và $\underset{x\to +\mathrm{\infty }}{lim}y=0;\underset{x\to -\mathrm{\infty }}{lim}y=+\mathrm{\infty }$.

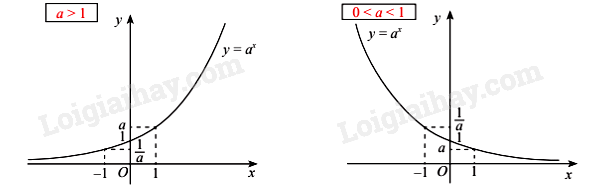
+ Đồ thị:

• Cắt trục tung tại điểm (0; 1), đi qua điểm (1; a).
• Nằm phía trên trục hoành.

2. Hàm số lôgarit

- Hàm số $y={\log }_{a}x\left(a>0;a\ne 1\right)$ được gọi là hàm số lôgarit cơ số a.

- Hàm số $y={\log }_{a}x\left(a>0;a\ne 1\right)$ có:

+ Tập xác định: $D=\left(0;+\mathrm{\infty }\right)$.

+ Tập giá trị: $T=\mathbb{R}$.

+ Hàm số liên tục trên $\left(0;+\mathrm{\infty }\right)$.

+ Sự biến thiên:

• Nếu a > 1 thì hàm số đồng biến trên $\left(0;+\mathrm{\infty }\right)$ và $\underset{x\to +\mathrm{\infty }}{lim}y=+\mathrm{\infty };\underset{x\to 0^{+}}{lim}y=0$.
• Nếu 0 < a < 1 thì hàm số nghịch biến trên $\left(0;+\mathrm{\infty }\right)$ và $\underset{x\to +\mathrm{\infty }}{lim}y=-\mathrm{\infty };\underset{x\to 0^{+}}{lim}y=+\mathrm{\infty }$.

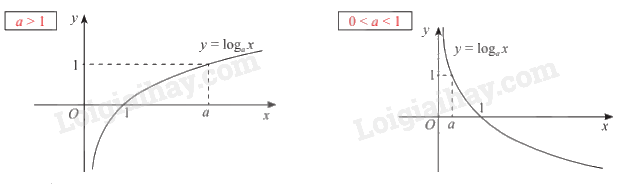
+ Đồ thị:

• Cắt trục hoành tại điểm (1; 0), đi qua điểm (a; 1).
• Nằm phía phải trục tung.

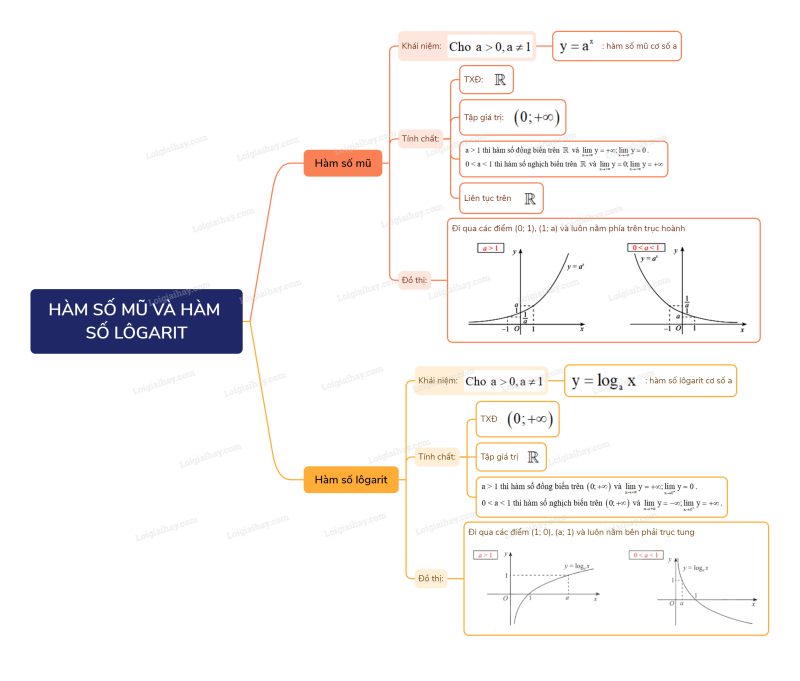
Sơ đồ tư duy Hàm số mũ. Hàm số lôgarit

B. Bài tập Hàm số mũ. Hàm số lôgarit

Đang cập nhật ...