Lý thuyết Phương trình, bất phương trình mũ và lôgarit (Chân trời sáng tạo 2024) Toán 11

Lý thuyết Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit - Chân trời sáng tạo

A. Lý thuyết Phương trình, bất phương trình mũ và lôgarit

1. Phương trình mũ cơ bản

Phương trình mũ cơ bản có dạng $a^x=b$(với $a>0,a\ne 1$).

- Nếu b > 0 thì phương trình có nghiệm duy nhất $x={\log }_{a}b$.

- Nếu b $\le$ 0 thì phương trình vô nghiệm.

Chú ý: Với $a>0,a\ne 1$

a) $a^x=a^{\alpha }\iff x=\alpha$.

b) Tổng quát hơn, $a^{u\left(x\right)}=a^{v\left(x\right)}\iff u\left(x\right)=v\left(x\right)$

Minh họa bằng đồ thị:

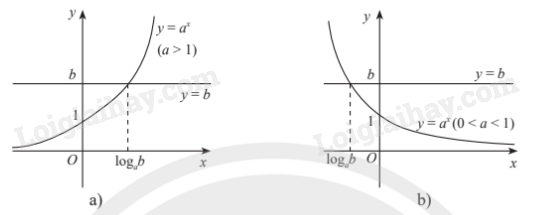
2. Phương trình lôgarit cơ bản

Phương trình lôgarit cơ bản có dạng ${\log }_{a}x=b\left(a>0,a\ne 1\right)$.

Phương trình luôn có nghiệm duy nhất $x=a^b$.

Chú ý: Với $a>0,a\ne 1$

a) ${\log }_{a}u\left(x\right)=b\iff u\left(x\right)=a^b$.

b) ${\log }_{a}u\left(x\right)={\log }_{a}v\left(x\right)\iff \{\begin{array}{l}u\left(x\right)>0\\ u\left(x\right)=v\left(x\right)\end{array}$.

Có thể thay $u\left(x\right)>0$ bằng $v\left(x\right)>0$ (chọn bất phương trình đơn giản hơn)

Minh họa bằng đồ thị:

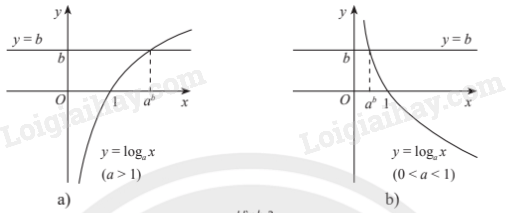
3. Bất phương trình mũ cơ bản

Bất phương trình mũ cơ bản có dạng $a^x>b$ (hoặc $a^x\ge b,a^x<b,a^x\le b$) với $a>0,a\ne 1$.

Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:

Nếu a > 1 thì $a^{u\left(x\right)}=a^{v\left(x\right)}\iff u\left(x\right)>v\left(x\right)$.

Nếu 0 < a < 1 thì $a^{u\left(x\right)}>a^{v\left(x\right)}\iff u\left(x\right)<v\left(x\right)$.

4. Bất phương trình lôgarit cơ bản

Bất phương trình lôgarit cơ bản có dạng ${\log }_{a}x>b$(hoặc ${\log }_{a}x\ge b,{\log }_{a}x<b,{\log }_{a}x\le b$) với $a>0,a\ne 1$.

Bảng tổng kết về nghiệm của các bất phương trình trên:

Chú ý:

Nếu a > 1 thì ${\log }_{a}u\left(x\right)>{\log }_{a}v\left(x\right)\iff \{\begin{array}{l}v\left(x\right)>0\\ u\left(x\right)>v\left(x\right)\end{array}$.

Nếu 0 < a < 1 thì ${\log }_{a}u\left(x\right)>{\log }_{a}v\left(x\right)\iff \{\begin{array}{l}u\left(x\right)>0\\ u\left(x\right)<v\left(x\right)\end{array}$.

Sơ đồ tư duy Phương trình, bất phương trình mũ và lôgarit

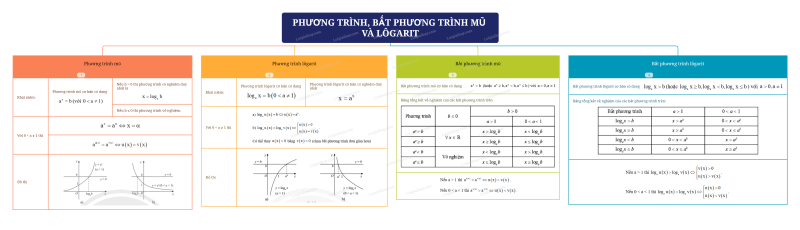
B. Bài tập Phương trình, bất phương trình mũ và lôgarit

Đang cập nhật ...