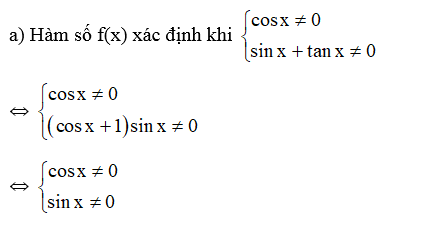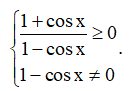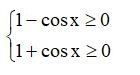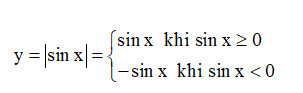Lý thuyết Hàm số lượng giác và đồ thị (Chân trời sáng tạo 2024) Toán 11
Tóm tắt lý thuyết Toán 11 Bài 4: Hàm số lượng giác và đồ thị ngắn gọn, chính xác sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 11.
Lý thuyết Toán 11 Bài 4: Hàm số lượng giác và đồ thị - Chân trời sáng tạo
Bài giảng Toán 11 Bài 4: Hàm số lượng giác và đồ thị
A. Lý thuyết Hàm số lượng giác và đồ thị
1. Hàm số lượng giác
Quy tắc đặt tương ứng mỗi số thực x với số thực sinx được gọi là hàm số sin, kí hiệu y = sinx. Tập xác định của hàm số sin là R.
Quy tắc đặt tương ứng mỗi số thực x với số thực cosx được gọi là hàm số cos, kí hiệu y = cosx. Tập xác định của hàm số côsin là R.
Hàm số cho bằng công thức y=sinαcosαđược gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là R∖{π2+kπ|k∈Z}.
Hàm số cho bằng công thức y=cosαsinα được gọi là hàm số tang, kí hiệu là y = tanx. Tập xác định của hàm số tang là R∖{kπ|k∈Z}.
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
a, Hàm số chẵn, hàm số lẻ
Cho hàm số y = f(x) có tập xác định là D.
Hàm số f(x) được gọi là hàm số chẵn nếu ∀x∈Dthì −x∈D và f(−x)=f(x). Đồ thị của một hàm số chẵn nhận trục tung (Oy) làm trục đối xứng.
Hàm số f(x) được gọi là hàm số lẻ nếu ∀x∈Dthì −x∈D và f(−x)=−f(x). Đồ thị của một hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
b, Hàm số tuần hoàn
Hàm số y = f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu tồn tại số T ≠ 0 sao cho với mọi x∈Dta có x±T∈D và f(x+T)=f(x)
Số T dương nhỏ nhất thỏa mãn cách điều kiện trên (nêu có) được gọi là chu kì của hàm số tuần hoàn đó.
* Nhận xét:
Các hàm số y = sinx, y=cosx tuần hoàn chu kì 2π.
Các hàm số y = tanx, y=cotx tuần hoàn chu kì π.
3. Đồ thị của các hàm số lượng giác
a, Hàm số y = sinx
Tập xác định là R.
Tập giá trị là [-1;1].
Là hàm số lẻ và tuần hoàn chu kì 2π.
Đồng biến trên mỗi khoảng (−π2+k2π;π2+k2π) và nghịch biến trên mỗi khoảng (π2+k2π;3π2+k2π).
Có đồ thị đối xứng qua gốc tọa độ và gọi là một đường hình sin.
b, Hàm số y = cosx
Tập xác định là R.
Tập giá trị là [-1;1].
Là hàm số chẵn và tuần hoàn chu kì 2π.
Đồng biến trên mỗi khoảng (−π+k2π;k2π) và nghịch biến trên mỗi khoảng (k2π;π+k2π).
Có đồ thị là một đường hình sin đối xứng qua trục tung.
c, Hàm số y = tanx
Tập xác định là R∖{π2+kπ|k∈Z}.
Tập giá trị là R.
Là hàm số lẻ và tuần hoàn chu kì π.
Đồng biến trên mỗi khoảng (−π2+kπ;π2+kπ), k∈Z.
Có đồ thị đối xứng qua gốc tọa độ.
d, Hàm số y = cotx
Tập xác định là R∖{kπ|k∈Z}.
Tập giá trị là R.
Là hàm số lẻ và tuần hoàn chu kì π.
Đồng biến trên mỗi khoảng (kπ;π+kπ), k∈Z.
Có đồ thị đối xứng qua gốc tọa độ.
B. Bài tập Hàm số lượng giác và đồ thị
Bài 1. Xét tính chẵn lẻ của các hàm số sau:
a) f(x)=x2sinx+tanx.
b) f(x) = |x|.sin x.
Hướng dẫn giải
⇔ sin 2x ≠ 0 ⇔ 2x ≠ kπ ⇔ x≠kπ2, k ∈ ℤ.
Vậy hàm số f(x) xác định trên 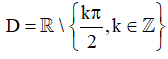
Ta có: f(−x)=(−x)2sin(−x)+tan(−x)=−x2sinx+tanx=−f(x)
Vậy hàm số f(x)=x2sinx+tanx là hàm số lẻ.
b) Hàm số f(x) xác định trên D = ℝ là tập đối xứng
Ta có: f(−x) = |−x|.sin (−x) = |x|.sin x = −f(x).
Vậy hàm số f(x) = |x|.sin x là hàm số lẻ.
Bài 2. Tìm tập xác định của hàm số: y=√1+cosx1−cosx.
Hướng dẫn giải
Hàm số y=√1+cosx1−cosx xác định ⇔
Vì −1≤cosx≤1, ∀x∈ℝ nên
⇒ 1+cosx1−cosx≥0, (1−cosx)≠0.
Do đó y xác định khi và chỉ khi 1−cosx≠0 ⇔ cos x ≠ 1 ⇔ x ≠ k2π.
Vậy tập xác định của hàm số là D = ℝ \ {k2π, k ∈ ℤ}.
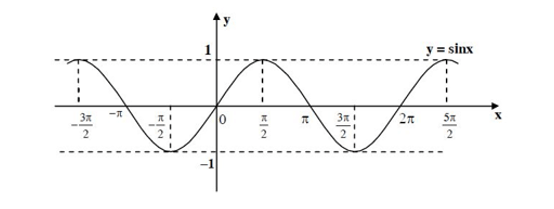
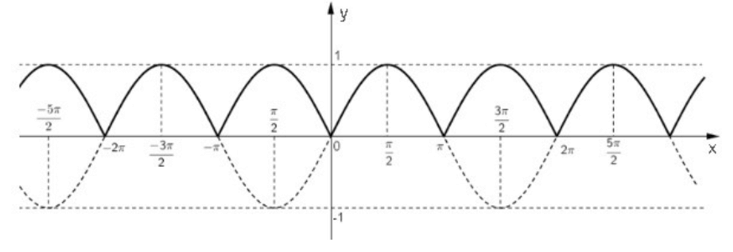
Bài 3. Dựa vào đồ thị của hàm số y = sin x, vẽ đồ thị của hàm số y = |sin x|.
Hướng dẫn giải
Ta biết đồ thị hàm số y = sin x có dạng như sau:
Với hàm số y = |sin x| ta có:
Từ dồ thị hàm số y = sin x ta có thể suy ra đồ thị hàm số y = |sin x| bằng cách:
- Giữ nguyên phần đồ thị nằm phía trên trục Ox (sin x > 0).
- Lấy đối xứng phần đồ thị nằm phía dưới Ox qua Ox.
Như vậy, ta được đồ thị hàm số y = |sin x| có dạng như sau (nét liền).