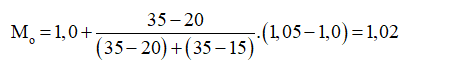Lý thuyết Trung vị và tứ phân vị của mẫu số liệu ghép nhóm (Chân trời sáng tạo 2024) Toán 11

Lý thuyết Toán 11 Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm - Chân trời sáng tạo

Bài giảng Toán 11 Bài 2: Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

A. Lý thuyết Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

1. Trung vị

Công thức xác định trung vị của mẫu số liệu ghép nhóm:

+) Gọi n là cỡ mẫu.

+) Giả sử đó là nhóm thứ p: $[u_m;u_{m+1})$.

+) $n_m$ là tần số của nhóm chứa trung vị.

+) $C=n_1+n_2+...+n_{m-1}$.

Khi đó trung vị là:

$M_e=u_m+\frac{\frac{n}{2}-C}{n_m}.\left(u_{m+1}-u_m\right)$

* Ý nghĩa: Từ dữ liệu ghép nhóm nói chung không thể xác định chính xác trung vị của mẫu số liệu gốc. Trung vị của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho mẫu số liệu gốc và có thể lấy làm giá trị đại diện cho mẫu số liệu.

2. Tứ phân vị

- Để tính tứ phân vị thứ nhất $Q_1$ của mẫu số liệu ghép nhóm, ta làm như sau:

• Giả sử nhóm chứa $Q_1$ là nhóm $[u_m;u_{m+1})$.
• $n_m$ là tần số của nhóm chứa phân vị thứ nhất.
• $C=n_1+n_2+...+n_{m-1}$.

Khi đó,

$Q_1=u_m+\frac{\frac{n}{4}-C}{n_m}.\left(u_{m+1}-u_m\right)$

- Để tính tứ phân vị thứ ba $Q_3$ của mẫu số liệu ghép nhóm, ta làm như sau:

• Giả sử nhóm chứa $Q_3$ là nhóm $[{\mathrm{u}}_j;u_{j+1})$.
• $n_j$là tần số của nhóm chứa phân vị thứ nhất.
• $C=n_1+n_2+...+n_{j-1}$.

Khi đó,

$Q_3=u_j+\frac{\frac{3n}{4}-C}{n_j}.\left(u_{j+1}-u_j\right)$

- Tứ phân vị thứ hai $Q_2$ chính là trung vị $M_e$.

- Nếu tứ phân vị thứ k là $\frac{1}{2}\left(x_m+x_{m+1}\right)$, trong đó $x_m$ và $x_{m+1}$thuộc hai nhóm liên tiếp thì ta lấy $Q_k=u_j$.

* Ý nghĩa:

Bộ ba tứ phân vị của mẫu số liệu ghép nhóm là giá tị xấp xỉ cho tứ phân vị của mẫu số liệu gốc và được sử dụng làm giá trị đo xu thế trung tâm của mẫu số liệu.

B. Bài tập Trung vị và tứ phân vị của mẫu số liệu ghép nhóm

Bài 1. Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:

Hãy ước lượng số trung bình, mốt và tứ phân vị của mẫu số liệu ghép nhóm trên.

Hướng dẫn giải

Số trung bình của dãy số liệu xấp xỉ bằng:

(0,925.10 + 0,975.20 + 1,025.35 + 1,075.15 + 1,125.5) : 85 = 1,016

Vậy nhóm chứa mốt của dãy số liệu là nhóm [1,0; 1,05).

Mốt của mẫu số liệu trên là:

Gọi x1; x2; x3;....; x85 lần lượt là số viên pin theo thứ tự không giảm.

Do x1,...., x10 ∈ [0,9; 0,95); x11,...., x30 ∈ [0,95; 1,0); x31,...., x65 ∈ [1,0; 1,05);

x66,...., x80 ∈ [1,05; 1,1); x81,...., x85 ∈ [1,1; 1,15).

Tứ phân vị thứ hai của dãy số liệu là $\frac{1}{2}\left({\mathrm{(x}}_{42}+x_{43}\right)$) thuộc nhóm [1,0; 1,05) nên tứ phân vị thứ hai của mẫu số liệu là $Q_2=1,0+\frac{\frac{85}{2}-30}{35}$(1,05-1,0) = 1,02

Tứ phân vị thứ nhất của dãy số liệu là $\frac{1}{2}\left({\mathrm{(x}}_{21}+x_{22}\right)$) thuộc nhóm [0,95; 1,0) nên tứ phân vị thứ nhất của mẫu số liệu là $Q_1=0,95+\frac{\frac{85}{4}-10}{20}$(1,0-0,95) = 0,98

Tứ phân vị thứ ba của dãy số liệu là $\frac{1}{2}\left({\mathrm{(x}}_{63}+x_{64}\right)$) thuộc nhóm [1,0; 1,05) nên tứ phân vị thứ ba của mẫu số liệu là $Q_3=1,0+\frac{\frac{3.85}{4}-30}{35}$(1,05- 1,0) = 1,048.

Vậy trong mẫu số liệu trên, số trung bình là 1,016, mốt là 1,02, tứ phân vị thứ nhất, thứ hai và thứ ba lần lượt là 0,98; 1,02; 1,048.

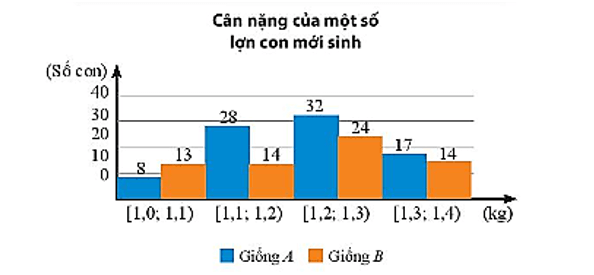
Bài 2. Cân nặng của một số lợn con mới sinh thuộc hai giống A và B được cho ở biểu đồ dưới đây (đơn vị: kg).

a) Hãy so sánh cân nặng của lợn con mới sinh giống A và giống B theo số trung bình và trung vị.

b) Hãy ước lượng tứ phân vị thứ nhất và thứ ba của cân nặng lợn con mới sinh giống A và của cân nặng lợn con mới sinh giống B.

Hướng dẫn giải

Cân nặng của lợn con giống A và giống B được thống kê như sau:

a) Số cân nặng trung bình của lợn con giống A là:

(1,05.8 + 1,15.28 + 1,25.32 + 1,35.17) : 85 = 1,22 (kg)

Số cân nặng trung bình của lợn con giống B là:

(1,05.13 + 1,15.14 + 1,25.24 + 1,35.14) : 65 = 1,21 (kg)

Vậy cân nặng trung bình của lợn con giống A lớn hơn lợn con giống B theo số trung bình.

Gọi x1; x2; x3;....; x85 lần lượt là số lợn con giống A theo thứ tự không giảm.

Do x1,...., x8 ∈ [1,0; 1,1); x9,...., x36 ∈ [1,1; 1,2); x37,...., x68 ∈ [1,2; 1,3);

x69,...., x85 ∈ [1,3; 1,4).

Trung vị của mẫu số liệu lợn con giống A thuộc nhóm [1,2; 1,3) là:

$M_A=1,2+\frac{\frac{85}{2}-36}{32}$.(1,3 - 1,2) = 1,22

Gọi y1; y2; y3;....; y65 lần lượt là số lợn con giống B theo thứ tự không giảm.

Do y1,...., y13 ∈ [1,0; 1,1); y14,...., y27 ∈ [1,1; 1,2); y28,...., y51 ∈ [1,2; 1,3);

y52,...., y65 ∈ [1,3; 1,4).

Trung vị của mẫu số liệu lợn con giống B thuộc nhóm [1,2; 1,3) là:

$M_B=1,2+\frac{\frac{65}{2}-27}{24}$.(1,3 - 1,2) =1,223

Vậy cân nặng trung bình của lợn con giống A nhỏ hơn lợn con giống B theo trung vị.

b) Tứ phân vị thứ nhất của dãy số liệu giống A là$\frac{1}{2}\left({\mathrm{(x}}_{21}+x_{22}\right)$) thuộc nhóm [1,1; 1,2) nên tứ phân vị thứ nhất của mẫu số liệu là $Q_{1A}=1,1+\frac{\frac{85}{4}-8}{28}$(1,2 - 1,1) = 1,15

Tứ phân vị thứ ba của dãy số liệu giống A là $\frac{1}{2}\left({\mathrm{(x}}_{63}+x_{64}\right)$) thuộc nhóm [1,2; 1,3) nên tứ phân vị thứ ba của mẫu số liệu là $Q_{3A}=1,2+\frac{\frac{3.85}{4}-36}{32}$(1,3 - 1,2) = 1,29

Tứ phân vị thứ nhất của dãy số liệu giống B là $\frac{1}{2}\left({\mathrm{(y}}_{16}+y_{17}\right)$) thuộc nhóm [1,1; 1,2) nên tứ phân vị thứ nhất của mẫu số liệu là $Q_{1B}=1,1+\frac{\frac{65}{4}-13}{14}$(1,2 - 1,1) = 1,12

Tứ phân vị thứ ba của dãy số liệu giống B là $\frac{1}{2}\left({\mathrm{(y}}_{48}+y_{49}\right)$) thuộc nhóm [1,2; 1,3) nên tứ phân vị thứ ba của mẫu số liệu là $Q_{3B}=1,2+\frac{\frac{3.65}{4}-27}{24}$(1,3 - 1,2) = 1,29

Vậy tứ phân vị thứ nhất của lợn con giống A và giống B lần lượt là 1,15 và 1,12;

Tứ phân vị thứ ba của lợn con giống A và giống B lần lượt là 1,29 và 1,29.