Lý thuyết Phép tính lũy thừa (Chân trời sáng tạo 2024) Toán 11
Tóm tắt lý thuyết Toán 11 Bài 1: Phép tính lũy thừa ngắn gọn, chính xác sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 11.
Nội dung bài viết
Xem thêm »
Lý thuyết Toán 11 Bài 1: Phép tính lũy thừa - Chân trời sáng tạo
A. Lý thuyết Phép tính lũy thừa
1. Lũy thừa với số mũ nguyên
- Lũy thừa với số mũ nguyên dương:
an=a.a.a...a⏟nthừasố(a∈R,n∈N∗).
- Lũy thừa với số mũ nguyên âm, số mũ 0:
a−n=1an;a0=1(n∈N∗,a∈R,a≠0).
2. Căn bậc n
Cho số thực b và số nguyên n≥2.
- Số a là căn bậc n của số b nếu an=b.
- Sự tồn tại căn bậc n:
+ Nếu n lẻ thì có duy nhất một căn bậc n của b, kí hiệu n√b.
+ Nếu n chẵn thì:
- b < 0: không tồn tại căn bậc n của b.
- b = 0: có một căn bậc n của b là 0.
- b > 0: có hai căn bậc n của b đối với nhau, kí hiệu giá trị dương là n√b và giá trị âm là −n√b.
+ Các tính chất:
- n√a.n√b=n√ab
- n√an√b=n√ab
- (n√a)m=n√am
- m√n√a=mn√a
3. Lũy thừa với số mũ hữu tỉ
Cho số thực dương a và số hữu tỉ r=mn, trong đó m,n∈Z,n>0. Ta có:
ar=amn=n√am
4. Lũy thừa với số mũ vô tỉ
Giả sử a là một số dương, α là một số vô tỉ và (rn) là một dãy số hữu tỉ sao cho lim. Khi đó .
5. Tính chất của phép tính lũy thừa
Cho a, b là những số thực dương; là những số thực bất kì. Khi đó:
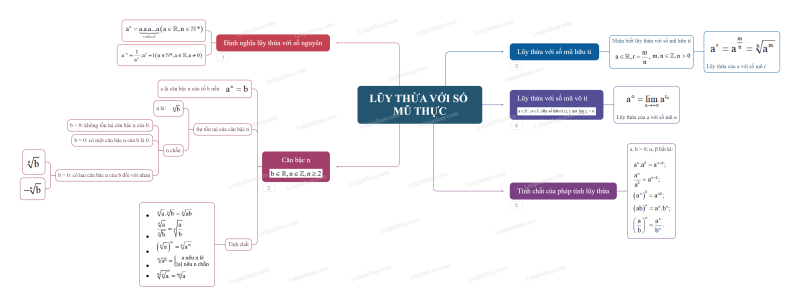
Sơ đồ tư duy Phép tính lũy thừa
B. Bài tập Phép tính lũy thừa
Đang cập nhật ...