Lý thuyết Đạo hàm (Chân trời sáng tạo 2024) Toán 11

Lý thuyết Toán 11 Bài 1: Đạo hàm - Chân trời sáng tạo

A. Lý thuyết Đạo hàm

1. Đạo hàm

Cho hàm số y = f(x) xác định trên khoảng $\left(a;b\right)$ và điểm $x_0\in \left(a;b\right)$.

Nếu tồn tại giới hạn (hữu hạn)

$\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$

thì giới hạn đó được gọi là đạo hàm của f(x) tại điểm $x_0$, kí hiệu là $f^{\prime }\left(x_0\right)$ hoặc $y^{\prime }\left(x_0\right)$.

Vậy:

$f^{\prime }\left(x_0\right)=\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$.

Chú ý:

- Cho hàm số y = f(x) xác định trên khoảng (a; b). Nếu hàm số này có đạo hàm tại mọi điểm $x\in \left(a;b\right)$ thì ta nói nó có đạo hàm trên khoảng (a; b), kí hiệu y’ hoặc f’(x).

- Cho hàm số y = f(x) xác định trên khoảng (a; b), có đạo hàm tại $x_0\in \left(a;b\right)$.

a) Đại lượng $\mathrm{\Delta }x=x-x_0$ gọi là số gia của biến tại $x_0$. Đại lượng $y=f\left(x\right)-f\left(x_0\right)$ gọi là số gia tương ứng của hàm số. Khi đó, $x=x_0+\mathrm{\Delta }x$ và

$f^{\prime }\left(x_0\right)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f\left(x_0+\mathrm{\Delta }x\right)-f\left(x_0\right)}{\mathrm{\Delta }x}$.

b) Tỉ số $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$ biểu thị tốc độ thay đổi trung bình của đại lượng y theo đại lượng x trong khoảng từ $x_0$ đến $x_0+\mathrm{\Delta }x$; còn $f^{\prime }\left(x_0\right)$ biểu thị tốc độ thay đổi (tức thời) của đại lượng y theo đại lượng x tại điểm $x_0$.

2. Ý nghĩa vật lí của đạo hàm

- Nếu hàm số s = f(t) biểu thị quãng đường di chuyển của vật theo thời gian t thì $f^{\prime }\left(t_0\right)$ biểu thị tốc độ tức thời của chuyển động tại thời điểm $t_0$.

- Nếu hàm số T = f(t) biểu thị nhiệt độ T theo thời gian t thì $f^{\prime }\left(t_0\right)$ biểu thị tốc độ thay đổi nhiệt độ theo thời gian tại thời điểm $t_0$.

3. Ý nghĩa hình học của đạo hàm

Đạo hàm của hàm số $y=f\left(x\right)$ tại điểm $x_0$ là hệ số góc của tiếp tuyến $M_{0}T$ với đồ thị (C) của hàm số tại điểm $M_0\left(x_0;f\left(x_0\right)\right)$.

Tiếp tuyến $M_{0}T$ có phương trình là $y-f\left(x_0\right)=f^{\prime }\left(x_0\right)\left(x-x_0\right)$.

Sơ đồ tư duy Đạo hàm

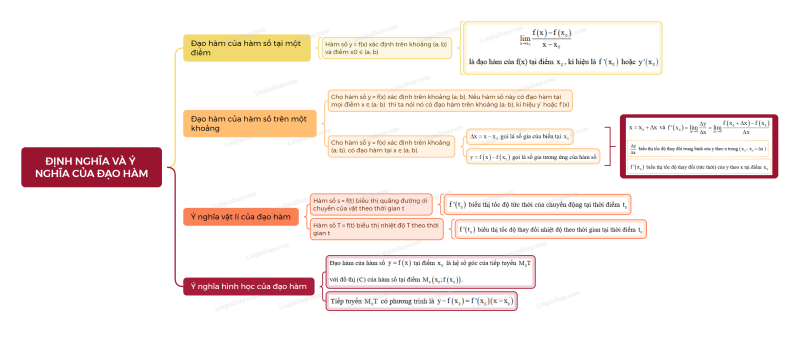
B. Bài tập Đạo hàm

Đang cập nhật ...