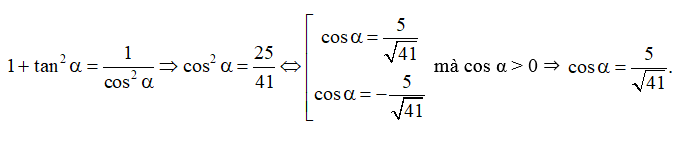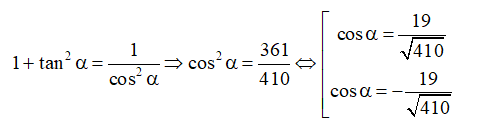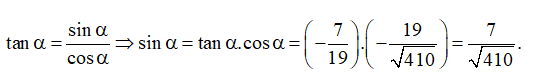Lý thuyết Giá trị lượng giác của một góc lượng giác (Chân trời sáng tạo 2024) Toán 11
Tóm tắt lý thuyết Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác ngắn gọn, chính xác sách Chân trời sáng tạo sẽ giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt Toán 11.
Nội dung bài viết
Xem thêm »
Lý thuyết Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác - Chân trời sáng tạo
Bài giảng Toán 11 Bài 2: Giá trị lượng giác của một góc lượng giác
A. Lý thuyết Giá trị lượng giác của một góc lượng giác
1. Giá trị lượng giác của góc lượng giác
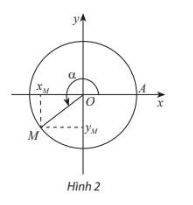
- Trên đường tròn, lấy điểm M(x;y) như hình vẽ. Khi đó:
x=x=cosαα, y=y=sinαα.
tanαα=sinαcosα=yx(x≠0)=sinαcosα=yx(x≠0)
cotα=cosαsinα=xy(y≠0)cotα=cosαsinα=xy(y≠0)
- Các giá trị sinαα, cosαα, tanαα, cotαα được gọi là các giá trị lượng giác của góc lượng giác αα.
*Chú ý:
a, Trục tung là trục sin, trục hoành là trục côsin.
Trục As có gốc ở điểm A(1;0) và song song với trục sin là trục tang.
Trục Bt có gốc ở điểm B(0;1) và song song với trục coossin gọi là trục côtang.
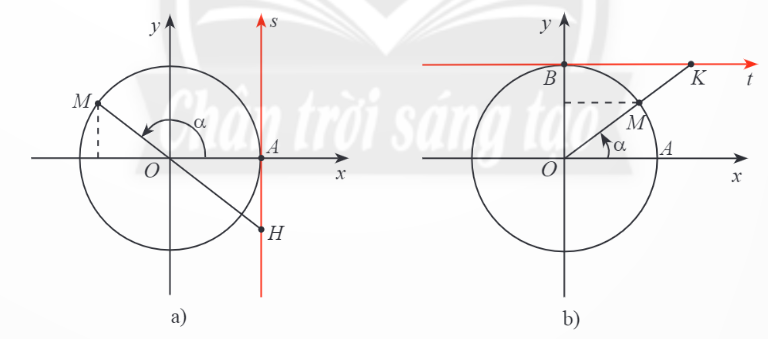
b, sinαsinαvà cosαcosα xác định với mọi α∈R.
tanαxác định với các góc α≠π2+kπ,k∈Z.
cotα xác định với các góc α≠kπ,k∈Z.
c, Với mọi góc lượng giác α và số nguyên k, ta có:
sin(α+k2π)=sinαcos(α+k2π)=cosαtan(α+kπ)=tanαcot(α+kπ)=cotα
d, Bảng các giá trị lượng giác đặc biệt
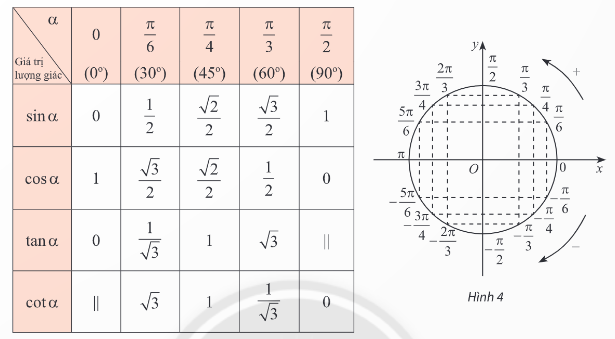
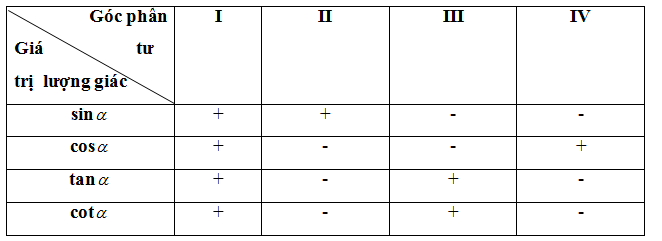
2. Tính giá trị lượng giác của một góc bằng máy tính cầm tay
- Lần lượt ấn các phím SHIFT →MENU →2:
Để chọn đơn vị độ: ấn phím 1 (Degree).
Để chọn đơn vị radian: ấn phím 2 (Radian).
- Ấn các phím MENU 1 để vào chế độ tính toán.
3. Hệ thức cơ bản giữa các giá trị lượng giác của một góc lượng giác
sin2α+cos2α=11+tan2α=1cos2α(α≠π2+kπ,k∈Z)1+cot2α=1sin2α(α≠kπ,k∈Z)tanα.cotα=1(α≠kπ2,k∈Z)
4. Giá trị lượng giác của các góc lượng giác có liên quan đặc biệt
- Hai góc đối nhau αvà −α
sin(−α)=−sinαcos(−α)=cosαtan(−α)=−tanαcot(−α)=−cotα
- Hai góc bù nhau (αvà π-α)
sin(π−α)=sinαcos(π−α)=−cosαtan(π−α)=−tanαcot(π−α)=−cotα
- Hai góc phụ nhau (αvà π2-α)
sin(π2−α)=cosαcos(π2−α)=sinαtan(π2−α)=cotαcot(π2−α)=tanα
- Hai góc hơn kém π(và π+α)
sin(π+α)=−sinαcos(π+α)=−cosαtan(π+α)=tanαcot(π+α)=cotα
B. Bài tập Giá trị lượng giác của một góc lượng giác
Bài 1. Tính các giá trị lượng giác của góc α biết:
a) tanα=−45 biết 3π2<α<2π.
b) cotα=−197 biết π2<α<π.
Hướng dẫn giải
a) Do 3π2<α<2π nên sin α < 0, cos α > 0, cot α < 0.
Ta có:
cotα=1tanα⇒cotα=−54.
tanα=sinαcosα⇒sinα=tanα.cosα=−45.5√41=−4√4141.
b) Do π2<α<π nên sin α > 0, cos α < 0, tan α < 0.
Ta có:
tanα=1cotα⇒tanα=−719.
Mà cos α < 0 ⇒ cosα=−19√410.
Bài 2. Cho tanα=35. Tính: A=sinαcosαsin2α−cos2α.
Hướng dẫn giải
Chia cả tử và mẫu của biểu thức A cho cos2α ta được:
A=sinαcosαsin2α−cos2α=tanαtan2α−1=−1516.
Bài 3. Rút gọn các biểu thức sau:
a) A = (1 – sin2α).cot2α + 1 – cot2α;
b) B=2cos2α−1sinα+cosα.
Hướng dẫn giải
a) A = (1 – sin2α).cot2α + 1 – cot2α
⇔ A = cot2α – sin2α.cot2α + 1 – cot2α
⇔ A=1−sin2α.cos2αsin2α=sin2α.
b) B=2cos2α−1sinα+cosα
⇔ B=cos2α−sin2αsinα+cosα
⇔ B = cos α – sin α.