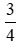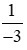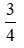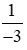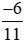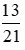Lý thuyết Mở rộng phân số. Phân số bằng nhau (Kết nối tri thức 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 23: Mở rộng phân số. Phân số bằng nhau

Video giải Toán 6 Bài 23: Mở rộng phân số. Phân số bằng nhau - Kết nối tri thức

I. Lý thuyết Mở rộng phân số. Phân số bằng nhau

1. Mở rộng khái niệm về phân số

– Định nghĩa về phân số: Với a, b ∈ ℤ, b ≠ 0 , ta gọi 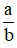 là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.

Ví dụ 1: 

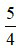 là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.

 là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.

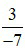 là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.

Chú ý: Mọi số nguyên đều có thể viết dưới dạng phân số.

Ví dụ 2: 

Số 3 có thể viết dưới dạng phân số là  .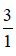

Số –8 có thể viết dưới dạng phân số là  .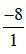

2. Hai phân số bằng nhau

Hai phân số  và 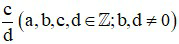 được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là  .

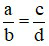Ví dụ 3: Hai phân số 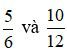  bằng nhau vì 5.12 = 60 và 6.10 = 60.

3. Tính chất cơ bản của phân số

– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

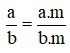 với a, b, m ∈ ℤ; b≠0; m≠0.

– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.

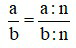 với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .

Ví dụ 4: 

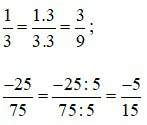
II. Bài tập vận dụng

Bài 1: Các cặp phân số sau đây có bằng nhau không? Vì sao?

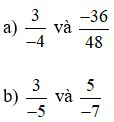
Lời giải:

a) Ta có: 3.48 = 144 và (–4).(–36) = 144

Vì 3.48 = (–4).(–36) = 144 nên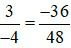 

b) Ta có: 3.(–7) = –21 và 5.(–5) = –25 

Vì 3.(–7) 5.(–5) (–21 –25) do đó:  .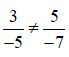

Bài 2: Hoàn thành bảng sau:

Lời giải: 

Bài 3: Cho các phân số 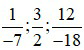 . Với mỗi phân số đã cho hãy tìm một phân số bằng nó sao cho phân số tìm được có mẫu số dương.

Lời giải:

+ Ta có: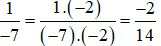 

Vậy phân số tìm được là  .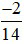

+ Ta có: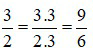 

Vậy phân số tìm được là  .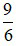

+ Ta có: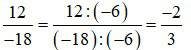 

Vậy phân số tìm được là  .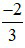

Bài giảng Toán 6 Bài 23: Mở rộng phân số. Phân số bằng nhau - Kết nối tri thức