Lý thuyết Quan hệ chia hết và tính chất (Kết nối tri thức 2024) Toán 6

Lý thuyết Toán lớp 6 Bài 8: Quan hệ chia hết và tính chất

Video giải Toán 6 Bài 8: Quan hệ chia hết và tính chất - Kết nối tri thức

A. Lý thuyết Quan hệ chia hết và tính chất

1. Quan hệ chia hết

Cho hai số tự nhiên a và b (b ≠ 0). 

Nếu có số tự nhiên k sao cho a = kb thì ta nói a chia hết cho b kí hiệu là a   b.

Nếu a không chia hết cho b ta kí hiệu là a 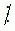  b.

Ví dụ 1. Tìm kí hiệu thích hợp ( 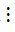; 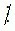)   điền vào chỗ trống:

a) 12   2;                               b) 105   5;                                      c) 26   4.

Lời giải

a) Ta có 12 = 2.6 nên 12 chia hết cho 2 ta viết 12    2.

b) Ta có 105 = 5.21 nên 105 chia hết cho 5 ta viết 105   5.

c) Ta có 26 không chia hết cho 4 nên ta viết 26 4.

+ Ước và bội:

Nếu a chia hết cho b, ta nói b là ước của a và a là bội của b.

Ta kí hiệu Ư(a) là tập hợp các ước của a và B(b) là tập hợp các bội của b.

Ví dụ 2. Khẳng định sau đây đúng hay sai?

a) 20 chia hết cho 5, 5 là ước của 20 và 20 là bội của 5.

b) 14 chia hết cho 3, 3 là ước của 14 và 14 là bội của 3.

c) 36 chia hết cho 9, 36 là ước của 9 và 9 là bội của 36.

Lời giải

a) Khẳng định a) đúng.

b) Vì 14 không chia hết cho 3 nên khẳng định b sai.

c) 36 chia hết cho 9 là đúng, trong đó 9 là ước của 36 và 36 là bội của 9 nên c sai.

+ Cách tìm ước và bội:

Muốn tìm các ước của a (a > 1), ta lần lượt chia a cho các số tự nhiên từ 1 đến a để xem a chia hết cho những số nào thì các số đó là ước của a.

Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lượt với 0; 1; 2; 3; …

Ví dụ 3. 

a) Hãy tìm tất cả các ước của 12.

b) Hãy tìm tất cả các bội của 8 nhỏ hơn 60.

Lời giải

a) Lần lượt chia 12 cho các số từ 1 đến 12, ta thấy 12 chia hết cho 1; 2; 3; 4; 6; 12 nên Ư(12) = {1; 2; 3; 4; 6; 12}.

b) Lần lượt nhân 8 với 0; 1; 2; 3; 4; 5; … ta được các bội của 8 là: 0; 8; 16; 24; 32; 40; 48; 56; 64; …

Các bội nhỏ hơn 60 của 8 là: 0; 8; 16; 24; 32; 40; 48; 56.

2. Tính chất chia hết của một tổng

+ Tính chất 1

Nếu tất cả các số hạng của một tổng đều chia hết cho cùng một số thì tổng chia hết cho số đó.

- Nếu a 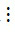  m và b  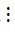 m thì (a + b)  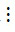 m.

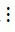- Nếu a   m, b 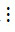  m và c  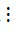 m thì (a + b + c)  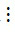 m.

Ví dụ 4. Không thực hiện phép tính, hãy cho biết:

a) 20 + 15 có chia hết cho 5 không. Vì sao?

b) 72 + 18 – 12 có chia hết cho 3 không. Vì sao?

Lời giải

a) Ta có 20 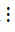 5 và 15  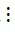 5 nên theo tính chất 1 thì tổng (20 + 1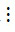5)   5.

b) Ta có 72 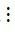 3, 18 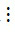 3 và 12  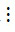3 nên theo tính chất 1 thì tổng (72 + 18 – 12) 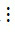 3.

+ Tính chất 2 

Nếu có một số hạng của một tổng không chia hết cho một số đã cho, các số hạng còn lại đều chia hết cho số đó thì tổng không chia hết cho số đã cho.

- Nếu a 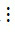 m và b  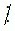m thì (a + b) 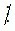m  .

- Nếu a 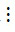 m, b m và c  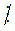m thì (a + b + c)  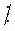 m.

Chú ý: Hai số không chia hết cho một số đã cho thì chưa chắc tổng của chúng không chia hết cho số đó.

Ví dụ 5. Các phát biểu sau đúng hay sai? 

a) 219.7 + 12 chia hết cho 7.

b) 2.3.4.11 + 22 + 45 không chia hết cho 11.

c) 8.12 + 9 chia hết cho 5.

Lời giải

a) Vì 219.7 là tích của 7 với số 219 nên chia hết cho 7 nhưng 12 không chia hết cho 7 nên 219.7 + 12   không chia hết cho 7. Do đó a sai.

b) Vì 2.3.4.11 là tích của 11 với các số 2; 3; 4 nên chia hết cho 11, 22 cũng chia hết cho 11 nhưng 45 không chia hết cho 11 nên 2.3.4.11 + 22 + 45 không chia hết cho 11. Do đó b đúng.

c) Ta có 8.12 không chia hết cho 5, 9 cũng không chia hết cho 5 nhưng tổng 8.12 + 9 = 105 lại chia hết cho 5. Do đó c đúng.

B. Bài tập

Bài 1. 

a) Tìm m thuộc tập {21; 22; 23; 24; 25; 26}, biết 56 – m chia hết 7;

b) Tìm n thuộc tập {18; 20; 22; 24; 26; 28; 30}, biết 36 + n không chia hết cho 6.

Lời giải

a) Vì 56 chia hết cho 7 để 56 – m chia hết cho 7 thì m phải là một số chia hết cho 7. 

Mà m thuộc tập {21; 22; 23; 24; 25; 26}

Suy ra m = 21.

Vậy m = 21.

b) Vì 36 chia hết cho 6 nên để 36 + n không chia hết cho 6 thì n phải không chia hết cho 6. 

Mà n thuộc tập {18; 20; 22; 24; 26; 28; 30}.

Suy ra n thuộc {20; 22; 26; 28}.

Vậy n ∈ {20; 22; 26; 28}.

Bài 2. Tìm các số tự nhiên x, y sao cho:

a) x ∈ B(12) và 10 < x < 40.

b) y ∈ Ư(20) và y ≥ 5 .

Lời giải

a) Ta có: B(12) = {0; 12; 24; 36; 48; …}

⇒ x ∈ {0; 12; 24; 36; ...}

Mà 10 < x < 40 nên x ∈ {12; 24; 36}.

Vậy x ∈ {12; 24; 36}.

b) Ta có: Ư(20) = {1; 2; 4; 5; 10; 20}

⇒ y ∈ {1; 2; 4; 5; 10; 20}

Mà y ≥ 5 nên y ∈ {5; 10; 20}.

Bài 3. Lớp 6A có 36 học sinh, cô giáo muốn chia đều số học sinh của lớp thành các nhóm để thực hiện các dự án học tập. Hoàn thành bảng sau vào vở:

Lời giải

Nếu số nhóm là 3 thì số người ở một nhóm là: 36:3 = 12 (người).

Nếu số người ở một nhóm là 9 thì số nhóm là: 36:9 = 4 (nhóm).

Nếu số nhóm là 6 thì số người ở một nhóm là: 36:6 = 6 (người).

Nếu số người ở một nhóm là 4 thì số nhóm là: 36:4 = 9 (người).

Nếu số người ở một nhóm là 3 thì số nhóm là: 36:3 = 12 (nhóm).

Ta có bảng sau:

Bài giảng Toán 6 Bài 8: Quan hệ chia hết và tính chất - Kết nối tri thức