Câu hỏi:
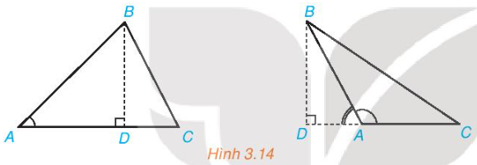
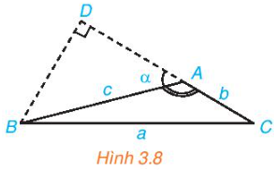
65 lượt xemHĐ 2 trang 38 Toán 10 Tập 1: Trong Hình 3.8, hãy thực hiện các bước sau để thiết lập công thức tính a theo b, c và giá trị lượng giác của góc A.
a) Tính a2 theo BD2 và CD2.
b) Tính a2 theo b, c và DA.
c) Tính DA theo c và cos A.
d) Chứng minh a2 = b2 + c2 – 2bc cos A.
Lời giải
Hướng dẫn giải:
Lời giải
a) Xét tam giác BDC vuông tại D, theo định lý Pythagore ta có:
BC2 = BD2 + DC2.
Hay a2 = BD2 + DC2 (1)
b) Xét ΔBDA vuông tại D, ta có:
BA2 = BD2 + DA2
Suy ra BD2 = BA2 – DA2 = c2 – DA2 (*)
Mà DC = DA + AC = DA + b nên DC2 = (DA + b)2 (**)
Thay (*) và (**) vào (1), ta được:
a2 = c2 – DA2 + (DA + b)2 = c2 – DA2 + DA2 + 2b . DA + b2
= c2 + b2 + 2b . DA.
Vậy a2 = c2 + b2 + 2b . DA (2)
c) Xét ΔBDA vuông tại D, ta có:
DA = c. cos α.
Mà cos α = cos (180o – A) = − cos A (do góc α và góc A bù nhau).
Do đó DA = − c. cos A.
d) Thay DA = − c. cos A vào biểu thức (2), ta được:
a2 = c2 + b2 + 2b . (− c. cos A)
= b2 + c2 − 2bc. cos A.
Vậy a2 = b2 + c2 − 2bc. cos A (đpcm).
Luyện tập 4 trang 41 Toán 10 Tập 1: Tính diện tích tam giác ABC có b = 2, .
Bài 3.6 trang 42 Toán 10 Tập 1: Cho tam giác ABC có a = 10, . Tính R, b, c.
Bài 3.7 trang 42 Toán 10 Tập 1: Giải tam giác ABC và tính diện tích tam giác đó, biết
