Câu hỏi:
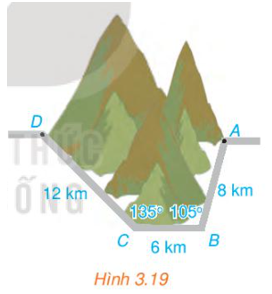
149 lượt xemVận dụng 2 trang 40 Toán 10 Tập 1: Từ một khu vực có thể quan sát hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Lời giải
Hướng dẫn giải:
Lời giải:
Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.
Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
* Tính AB bằng cách:
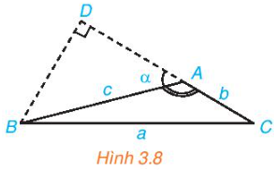
+ Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc α.
+ Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc β.
Ta có hình vẽ:
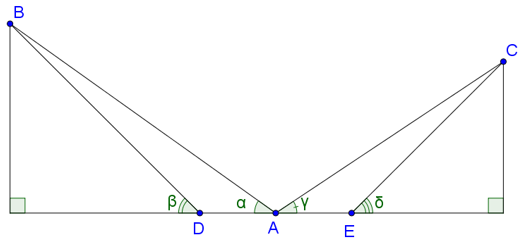
Ta có: ; .
Áp dụng định lí sin vào ∆ABD, ta được:
.
* Tương tự ngắm và đo để xác định AC.
Ta có: ; .
Áp dụng định lí sin vào ∆ACE, ta được:
.
Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí côsin cho tam giác ABC để tính độ dài cạnh BC.
Ta có: BC2 = AB2 + AC2 – 2AB.AC.cosBAC.
Với AB, AC, góc BAC đã biết ở các bước trên, thay vào ta tính được BC chính là khoảng cách giữa hai đỉnh núi.
Luyện tập 4 trang 41 Toán 10 Tập 1: Tính diện tích tam giác ABC có b = 2, .
Bài 3.6 trang 42 Toán 10 Tập 1: Cho tam giác ABC có a = 10, . Tính R, b, c.