30 câu Trắc nghiệm Đường vuông góc và đường xiên (có đáp án 2024) – Toán 7 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 8: Đường vuông góc và đường xiên đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 8.
Trắc nghiệm Toán 7 Bài 8: Đường vuông góc và đường xiên
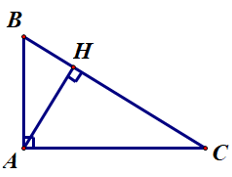
Câu 1. Cho ∆ABC có ^ABC=30°, . Gọi H là chân đường vuông góc kẻ từ B. Khẳng định nào sau đây đúng?
A. HA > AC;
B. HA < AC;
C. HA = AC;
D. .
Đáp án đúng là: B
Ta xét đáp án D:
∆ABC có: (định lí tổng ba góc của một tam giác)
Suy ra .
Do đó đáp án D sai.
Ta xét đáp án A, B, C:
Ta có AH là đường vuông góc kẻ từ điểm A đến đường thẳng BC; AC là một đường xiên kẻ từ điểm A đến đường thẳng AC.
Do đó AH < AC.
Suy ra đáp án B đúng, đáp án A, C sai.
Vậy ta chọn đáp án B.
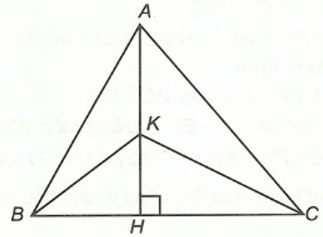
Câu 2. Cho ∆ABC (AB < AC), đường cao AH (H ∈ BC). Lấy điểm K bất kì thuộc AH (K ≠ H). Trong các đoạn thẳng AB, AC, AH, BK, CK, KH, đoạn thẳng nào ngắn nhất?
A. AH;
B. KH;
C. BK;
D. CK.
Đáp án đúng là: B
Ta có đoạn thẳng AH là đường vuông góc kẻ từ điểm A đến đường thẳng BC; các đoạn thẳng AB, AC là các đường xiên kẻ từ điểm A đến đường thẳng BC.
Do đó AH là đoạn thẳng ngắn nhất trong ba đoạn thẳng AB, AC và AH (1).
Ta có đoạn thẳng KH là đường vuông góc kẻ từ điểm K đến đường thẳng BC; các đoạn thẳng KB, KC là các đường xiên kẻ từ điểm K đến đường thẳng BC.
Do đó KH là đoạn thẳng ngắn nhất trong ba đoạn thẳng KB, KC và KH (2).
Vì K thuộc AH (giả thiết) nên KH < AH (3).
Từ (1), (2), (3), ta suy ra KH là đoạn thẳng ngắn nhất trong các đoạn thẳng AB, AC, AH, BK, CK, KH.
Vậy ta chọn đáp án B.
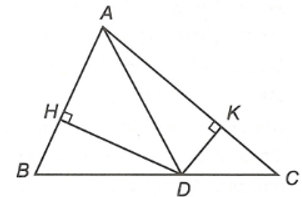
Câu 3. Cho ∆ABC, điểm D nằm giữa B và C. Gọi H, K lần lượt là chân các đường vuông góc kẻ từ điểm D xuống các đường thẳng AB, AC.
So sánh BC và tổng DH + DK.
A. DH + DK > BC;
B. DH + DK < BC;
C. DH + DK = BC;
D. Không thể so sánh được.
Đáp án đúng là: B
Ta có DH là đường vuông góc kẻ từ điểm D đến đường thẳng AB; DB là đường xiên kẻ từ điểm D đến đường thẳng AB.
Ta suy ra DH < DB (1).
Tương tự, ta có DK là đường vuông góc kẻ từ điểm D đến đường thẳng AC; DC là đường xiên kẻ từ điểm D đến đường thẳng AC.
Ta suy ra DK < DC (2).
Từ (1), (2), ta suy ra DH + DK < DB + DC = BC.
Khi đó ta có DH + DK < BC.
Vậy ta chọn đáp án B.
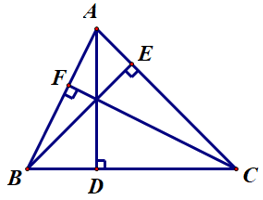
Câu 4. Cho ∆ABC. Vẽ AD ⊥ BC, BE ⊥ AC, CF ⊥ AB (D ∈ BC, E ∈ AC, F ∈ AB). So sánh AD + BE + CF và chu vi C của ∆ABC.
A. AD + BE + CF = C;
B. AD + BE + CF < C;
C. AD + BE + CF > C;
D. Không thể so sánh được.
Đáp án đúng là: B
Ta thấy AD là đường vuông góc kẻ từ điểm A đến đường thẳng BC và AB là một đường xiên kẻ từ điểm A đến đường thẳng BC.
Do đó AD < AB (1).
Tương tự, ta có CF là đường vuông góc kẻ từ điểm C đến đường thẳng AB và CA là một đường xiên kẻ từ điểm C đến đường thẳng AB.
Do đó CF < AC (2).
Tương tự, ta có BE là đường vuông góc kẻ từ điểm B đến đường thẳng AC và BC là một đường xiên kẻ từ điểm B đến đường thẳng AC.
Do đó BE < BC (3).
Lấy (1) + (2) + (3) vế theo vế, ta được:
AD + CF + BE < AB + AC + BC.
Do đó AD + BE + CF < C.
Vậy ta chọn đáp án B.
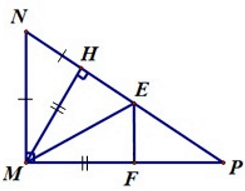
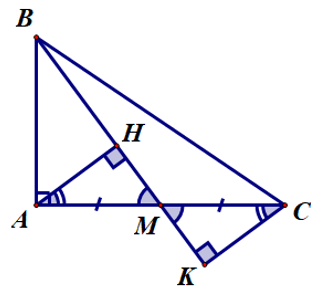
Câu 5. Cho ∆MNP vuông tại M. Vẽ MH ⊥ NP tại H. Trên cạnh NP lấy điểm E sao cho NE = MN. Trên cạnh MP lấy điểm F sao cho MF = MH. Khoảng cách từ E đến đường thẳng MP là đoạn thẳng:
A. EM;
B. EF;
C. EP;
D. EN.
Đáp án đúng là: B
Ta có NE = MN (giả thiết).
Suy ra ∆MNE cân tại N.
Do đó (1).
Vì ∆MNP vuông tại A nên .
Suy ra (2).
Từ (1), (2), ta suy ra (*).
∆MHE vuông tại H: (**).
Từ (*), (**), ta suy ra .
Xét ∆HME và ∆FME, có:
ME là cạnh chung.
(chứng minh trên).
MH = MF (giả thiết).
Do đó ∆HME = ∆FME (c.g.c).
Suy ra (cặp góc tương ứng).
Mà (do MH ⊥ HE).
Suy ra .
Do đó EF ⊥ MF hay EF ⊥ MP.
Khi đó ta có EF là đường vuông góc kẻ từ điểm E đến đường thẳng MP.
Do đó đoạn thẳng EF là khoảng cách từ E đến đường thẳng MP.
Vậy ta chọn đáp án B.
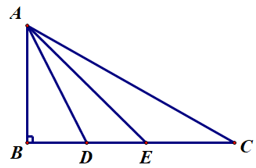
Câu 6. Cho hình bên.
Độ dài đoạn thẳng nào ngắn nhất?
A. AB;
B. AD;
C. AE;
D. AC.
Đáp án đúng là: A
Đoạn thẳng AB là đường vuông góc kẻ từ O đến đường thẳng BC.
Các đoạn thẳng AD, AE, AC là đường xiên kẻ từ A đến đường thẳng BC.
Do đó đoạn AB ngắn nhất.
Vậy ta chọn đáp án A
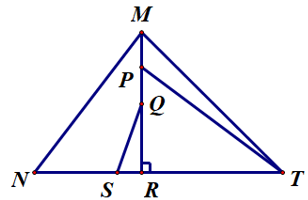
Câu 7. Trong hình bên có bao nhiêu đường xiên kẻ từ các điểm M, P, Q đến đường thẳng NT?
A. 2;
B. 3;
C. 4;
D. 5.
Đáp án đúng là: C
Các đường thẳng không vuông góc với NT đều là đường xiên từ các điểm không thuộc đường thẳng NT đến đường thẳng NT.
Các đoạn thẳng MN, MT là các đường xiên kẻ từ điểm M đến đường thẳng NT.
Đoạn thẳng PT là đường xiên kẻ từ điểm P đến đường thẳng NT.
Đoạn thẳng QS là đường xiên kẻ từ điểm Q đến đường thẳng NT.
Do đó có 4 đường xiên kẻ từ các điểm M, P, Q đến đường thẳng NT.
Vậy ta chọn đáp án C.
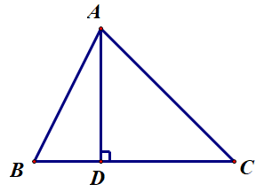
Câu 8. Cho ∆ABC có AD là đường cao như hình bên.
Trong ba cạnh AB, AD, AC, cạnh nào ngắn nhất?
A. AD;
B. AB;
C. AC;
D. Không thể so sánh được.
Đáp án đúng là: A
Ta có đoạn thẳng AD là đường vuông góc kẻ từ điểm A đến đường thẳng BC; các đoạn thẳng AB, AC là các đường xiên kẻ từ điểm A đến đường thẳng BC.
Do đó đoạn thẳng AD ngắn nhất.
Vậy ta chọn đáp án A.
Câu 9. Cho ∆ABC vuông tại A. Kẻ AH ⊥ BC (H ∈ BC). Có bao nhiêu đường vuông góc kẻ từ các điểm A, B, C đến các đường thẳng có trong hình bên?
A. 3;
B. 4;
C. 5;
D. 7.
Đáp án đúng là: C
Ta xét điểm A:
Đoạn thẳng AH là đường vuông góc kẻ từ điểm A đến đường thẳng BC.
Do đó có 1 đường vuông góc kẻ từ điểm A trong hình trên (1).
Ta xét điểm B:
+) Đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC.
+) Đoạn thẳng BH là đường vuông góc kẻ từ điểm B đến đường thẳng AH.
Do đó có 2 đường vuông góc kẻ từ điểm B trong hình trên (2).
Ta xét điểm C:
+) Đoạn thẳng CA là đường vuông góc kẻ từ điểm C đến đường thẳng AB.
+) Đoạn thẳng CH là đường vuông góc kẻ từ điểm C đến đường thẳng AH.
Do đó có 2 đường vuông góc kẻ từ điểm C trong hình trên (3).
Từ (1), (2), (3), ta được 5 đường vuông góc thỏa yêu cầu bài toán.
Vậy ta chọn đáp án C.
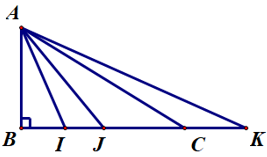
Câu 10. Cho ∆ABC vuông tại B. Trên đường thẳng BC lấy điểm I, J, K sao cho AI < AJ < AK. Hỏi B là hình chiếu của các điểm nào lên đường thẳng AB?
A. C, J, A, K;
B. A, C, K, J;
C. I, J, C, A;
D. I, J, C, K.
Đáp án đúng là: D
Trong hình trên, ta thấy CB ⊥ AB (∆ABC vuông tại B).
Do đó B là hình chiếu của C lên đường thẳng AB.
Ta có I, J, K đều thuộc đường thẳng BC.
Mà BC ⊥ AB.
Do đó IB ⊥ AB hay JB ⊥ AB hay KB ⊥ AB.
Suy ra B là hình chiếu của I, J, K lên đường thẳng AB.
Khi đó ta có B là hình chiếu của các điểm I, J, K, C lên đường thẳng AB.
Vậy ta chọn đáp án D.
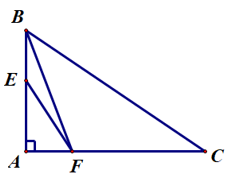
Câu 11. Cho ∆ABC vuông tại A. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm F. So sánh độ dài các cạnh EA và BF.
A. EA = BF;
B. EA < BF;
C. EA > BF;
D. Không thể so sánh được.
Đáp án đúng là: B
Ta có đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC; đoạn thẳng BF là đường xiên kẻ từ điểm B đến đường thẳng AC.
Do đó BA < BF (1).
Vì E thuộc cạnh AB (giả thiết) nên EA < BA (2).
Từ (1), (2), ta suy ra EA < BA < BF.
Vậy ta chọn đáp án B.
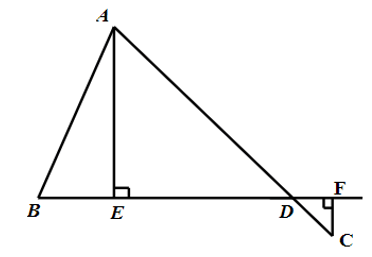
Câu 12. Cho hình vẽ bên.
So sánh AC và AE + CF.
A. AC > AE + CF;
B. AC < AE + CF;
C. AC = AE + CF;
D. Không thể so sánh được.
Đáp án đúng là: A
Ta có đoạn thẳng AE là đường vuông góc kẻ từ điểm A đến đường thẳng EF; đoạn thẳng AD là đường xiên kẻ từ điểm A đến đường thẳng EF.
Do đó AE < AD (1).
Ta có đoạn thẳng CF là đường vuông góc kẻ từ điểm C đến đường thẳng EF; đoạn thẳng CD là đường xiên kẻ từ điểm C đến đường thẳng EF.
Do đó CF < CD (2).
Lấy (1) + (2) vế theo vế, ta được AE + CF < AD + CD = AC.
Vậy ta chọn đáp án A.
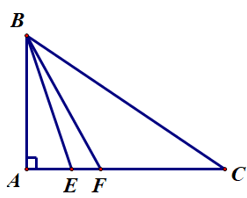
Câu 13. Cho ∆ABC vuông tại A, biết AB = 10 cm. Trên đường thẳng AC, lấy hai điểm E và F sao cho AE = 3 cm, AF = 5 cm. So sánh CA, CB, CE và CF.
A. CF < CE < CA < CB;
B. CB < CF < CA < CE;
C. CE < CA < CB < CF;
D. CF < CA < CE < CB.
Đáp án đúng là: A
Ta thấy CA ⊥ AB tại A.
Do đó CA là đường vuông góc kẻ từ điểm C đến đường thẳng AB và BC là đường xiên kẻ từ điểm C đến đường thẳng AB.
Suy ra CA < CB (1).
Ta có E ∈ AC và AE = 3 cm.
Suy ra CE = AC – AE = AC – 3.
Do đó CE < AC (2).
Ta có F ∈ AC và AF = 5 cm.
Suy ra CF = AC – AF = AC – 5 = (AC – 3) – 2.
Mà CE = AC – AE = AC – 3 (chứng minh trên).
Do đó CF = CE – 2
Suy ra CF < CE (3).
Từ (1), (2), (3), ta suy ra CF < CE < CA < CB.
Vậy ta chọn đáp án A.
Câu 14. Cho ∆ABC vuông tại A. Gọi M là trung điểm AC. Kẻ AH ⊥ BM tại H, CK ⊥ BM tại K. So sánh AB và .
A. ;
B. ;
C. ;
D. Không thể so sánh được.
Đáp án đúng là: B
Ta có AH ⊥ BM (giả thiết) và CK ⊥ BM (giả thiết).
Suy ra AH // CK.
Do đó (cặp góc so le trong).
Xét ∆HAM và ∆KCM, có:
(hai góc đối đỉnh).
MA = MC (M là trung điểm AC).
(chứng minh trên).
Do đó ∆HAM = ∆KCM (g.c.g).
Suy ra MH = MK (cặp cạnh tương ứng).
Ta có đoạn thẳng BA là đường vuông góc kẻ từ điểm B đến đường thẳng AC; đoạn thẳng BM là đường xiên kẻ từ điểm B đến đường thẳng AC.
Suy ra BA < BM.
Do đó BA < BH + HM (1) và BA < BK – MK (2).
Lấy (1) + (2) vế theo vế ta được 2BA < BH + HM + BK – MK.
Mà HM = MK (chứng minh trên).
Do đó 2AB < BH + BK.
Suy ra .
Vậy ta chọn đáp án B.
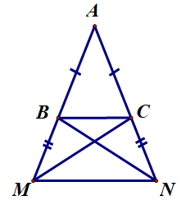
Câu 15. Hình bên mô tả một chiếc thang đứng hình chữ A là tam giác ABC. Do chiếc thang hơi ngắn nên một người thợ đã nối thêm 2 thanh gỗ bằng nhau BM và CN lần lượt vào hai cạnh AB, AC. Để giữ thăng bằng và cố định chiếc thang nên người thợ này muốn đóng thêm 2 thanh gỗ bằng nhau là BN và CM. Biết BC = 0,6 m, MN = 0,9 m. Em hãy cho biết độ dài thanh gỗ BN cần dài ít nhất bao nhiêu là hợp lí?
A. 0,3 m;
B. 0,6 m;
C. 0,75 m;
D. 0,8 m.
Đáp án đúng là: D
Ta có AB = AC (do ∆ABC cân tại A) và BM = CN (giả thiết).
Suy ra AB + BM = AC + CN.
Do đó AM = AN.
Suy ra ∆AMN cân tại A.
Vì vậy .
Ta có (tổng ba góc trong một tam giác).
Suy ra .
Do đó (1).
Ta có ∆ABC cân tại A.
Suy ra .
Ta có (tổng ba góc trong một tam giác).
Suy ra
Do đó (2).
Từ (1), (2), ta suy ra .
Mà hai góc này ở vị trí đồng vị.
Khi đó ta có BC // MN.
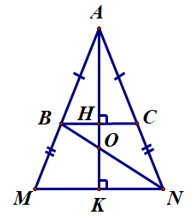
Kẻ AH ⊥ BC tại H. Suy ra AH ⊥ MN
Giả sử AH ⊥ MN tại K.
Xét ∆ABH và ∆ACH, có:
.
(do ∆ABC cân tại A).
AB = AC (do ∆ABC cân tại A).
Do đó ∆ABH = ∆ACH (cạnh huyền – góc nhọn).
Suy ra HB = HC (cặp cạnh tương ứng).
Do đó H là trung điểm BC.
Khi đó ta có .
Tương tự ta có .
Gọi O là giao điểm của BN và AK.
Theo quan hệ giữa đường vuông góc và đường xiên, ta có:
BO > và ON > .
Suy ra BN = BO + ON >
Mà .
Do đó BN > 0,75 (m).
Vì 0,8 (m) > 0,75 (m).
Nên ta chọn đáp án D.