30 câu Trắc nghiệm Tính chất ba đường trung trực của tam giác (có đáp án 2024) – Toán 7 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 12: Tính chất ba đường trung trực của tam giác đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 12.
Trắc nghiệm Toán 7 Bài 12: Tính chất ba đường trung trực của tam giác
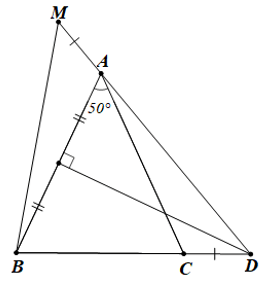
Câu 1. Cho ∆ABC cân tại A, có ˆA=50°. Đường trung trực của cạnh AB cắt BC tại D. Trên tia đối của tia AD, lấy điểm M sao cho AM = CD. Khẳng định nào sau đây đúng nhất?
A. ;
B. ∆BMD cân tại M;
C. ∆BMD cân tại B;
D. ∆BMD đều.
Đáp án đúng là: C
Vì D thuộc đường trung trực của cạnh AB.
Nên D cách đều hai đầu mút A và B.
Suy ra DA = DB.
Do đó ∆ABD cân tại D.
Vì vậy (tính chất tam giác cân)
Vì ∆ABC cân tại A nên .
∆ABC có: (tổng ba góc trong một tam giác)
Suy ra .
Do đó .
Vì vậy .
Suy ra .
Do đó .
Vì vậy đáp án A sai.
Ta có (hai góc kề bù).
Suy ra (1).
Ta có (hai góc kề bù).
Suy ra (2).
Từ (1), (2), ta suy ra .
Xét ∆ABM và ∆CAD, có:
AM = CD (giả thiết).
(chứng minh trên).
AB = AC (do ∆ABC cân tại A).
Do đó ∆ABM = ∆CAD (c.g.c)
Suy ra BM = AD (cặp cạnh tương ứng).
Mà DB = DA (chứng minh trên).
Do đó BM = DB.
Suy ra ∆BMD cân tại B.
Do đó đáp án C đúng.
∆ACD có: (tổng ba góc trong một tam giác)
Suy ra .
Vì vậy ∆BMD không phải là tam giác đều.
Do đó đáp án B và D sai.
Vậy ta chọn đáp án C.
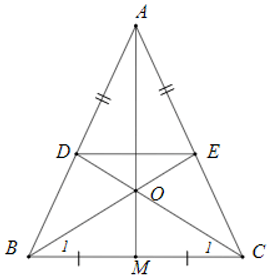
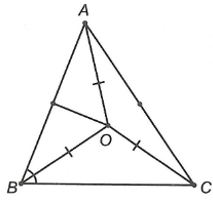
Câu 2. Cho ∆ABC cân tại A. Trên các cạnh AB, AC lần lượt lấy các điểm D và E sao cho AD = AE, CD cắt BE tại O. Gọi M là trung điểm BC. Khẳng định nào sau đây đúng nhất?
A. ∆BOC cân tại O;
B. Ba điểm A, O, M thẳng hàng;
C. AM, BE, CD đồng quy tại một điểm;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Ta có AB = AC (do ∆ABC cân tại A) và AD = AE (giả thiết).
Suy ra AB – AD = AC – AE.
Do đó BD = CE.
Xét ∆EBC và ∆DCB, có:
BC là cạnh chung.
(do ∆ABC cân tại A).
BD = CE (chứng minh trên).
Do đó ∆EBC = ∆DCB (c.g.c)
Suy ra (cặp góc tương ứng).
Suy ra ∆BOC cân tại O.
Do đó đáp án A đúng.
Ta có ∆BOC cân tại O.
Suy ra OB = OC.
Mà AB = AC (chứng minh trên)
Do đó AO là đường trung trực của cạnh BC (1).
Xét tam giác ABM và tam giác ACM có:
AB = AC (chứng minh trên),
(do ∆ABC cân tại A),
BM = CM (do M là trung điểm BC)
Do đó ∆ABM = ∆ACM (c.g.c)
Suy ra (hai góc tương ứng)
Mà (hai góc kề bù)
Do đó
Suy ra AM ⊥ BC tại trung điểm M của BC
Khi đó AM là đường trung trực của BC (2)
Từ (1), (2), ta suy ra A, O, M thẳng hàng.
Do đó đáp án B đúng.
Ta có O thuộc AM (chứng minh trên).
Mà O là giao điểm của BE và CD.
Suy ra ba đường thẳng AM, BE, CD đồng quy tại điểm O.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
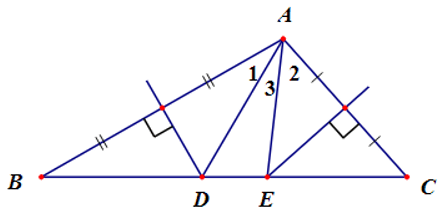
Câu 3. Cho ∆ABC có là góc tù. Các đường trung trực của cạnh AB và AC cắt nhau tại O và cắt BC theo thứ tự tại D và E. Khẳng định nào sau đây đúng nhất?
A. ∆ABD cân tại D;
B. ∆ACE cân tại E;
C. ∆OAB cân tại O;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Gọi M, N lần lượt là trung điểm của AB, AC.
Vì D thuộc đường trung trực OM của cạnh AB.
Nên D cách đều A và B.
Do đó DB = DA.
Suy ra ∆ABD cân tại D.
Do đó đáp án A đúng.
Chứng minh tương tự, ta được ∆ACE cân tại E và ∆OAB cân tại O.
Do đó đáp án B, C đúng.
Vậy ta chọn đáp án D.
Câu 4. Cho ∆ABC có tù. Các đường trung trực của AB và AC cắt BC lần lượt tại D và E. Biết
. Số đo
bằng:
A. 95°;
B. 100°;
C. 105°;
D. 115°.
Đáp án đúng là: C
Vì điểm D nằm trên đường trung trực của AB nên DA = DB.
Suy ra ∆DAB cân tại D.
Do đó .
Chứng minh tương tự, ta được .
Do đó .
Xét tam giác ABC có: (tổng ba góc trong một tam giác)
Vậy ta chọn đáp án C.
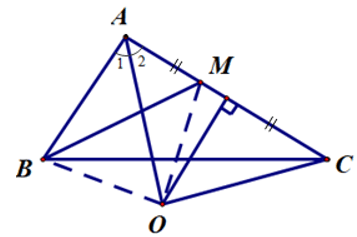
Câu 5. Cho ∆ABC có AB < AC. Trên cạnh AC lấy điểm M sao cho CM = AB. Vẽ đường trung trực của AC, cắt tia phân giác của tại điểm O. Đường trung trực của đoạn thẳng BM đi qua điểm:
A. O;
B. A;
C. M;
D. C.
Đáp án đúng là: A
Điểm O nằm trên đường trung trực của cạnh AC nên OA = OC.
Suy ra ∆OAC cân tại O.
Do đó .
Vì AO là tia phân giác của nên .
Do đó ().
Xét ∆ABO và ∆CMO, có:
AO = CO (chứng minh trên),
(chứng minh trên),
AB = CM (giả thiết).
Do đó ∆ABO = ∆CMO (c.g.c)
Suy ra OB = OM (cặp cạnh tương ứng).
Do đó O nằm trên đường trung trực của cạnh BM.
Vậy ta chọn đáp án A.
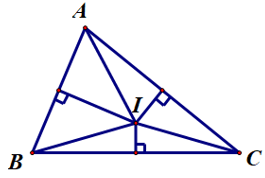
Câu 6. Cho ∆ABC, gọi I là giao điểm của hai đường trung trực của hai cạnh AB và AC. Kết quả nào dưới đây đúng?
A. IA > IB > IC;
B. IA = IB = IC;
C. IA < IB < IC;
D. Không thể so sánh được độ dài của IA, IB, IC.
Đáp án đúng là: B
∆ABC có I là giao điểm của hai đường trung trực của hai cạnh AB và AC.
Suy ra I cũng thuộc đường trung trực của cạnh BC.
Vì giao điểm I của ba đường trung trực cách đều ba đỉnh của ∆ABC.
Nên IA = IB = IC.
Vậy ta chọn đáp án B.
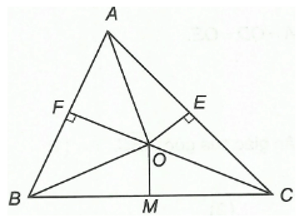
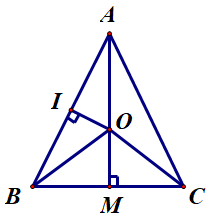
Câu 7. Cho ∆ABC có M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại O. Số đo bằng:
A. 30°;
B. 45°;
C. 60°;
D. 90°.
Đáp án đúng là: D
Vì ba đường trung trực của ∆ABC cùng đi qua một điểm nên giao điểm O của hai đường trung trực của các cạnh AB, AC cũng thuộc đường trung trực của cạnh BC.
Do đó OM là đường trung trực thứ ba của ∆ABC.
Suy ra OM ⊥ BC.
Nên .
Vậy ta chọn đáp án D.
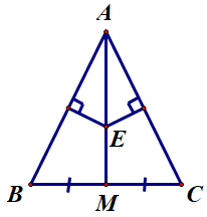
Câu 8. Cho ∆ABC cân tại A. Gọi M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại E. Điểm E thuộc đường thẳng nào trong các đường thẳng sau đây.
A. BC;
B. AM;
C. AB;
D. AC.
Đáp án đúng là: B
Xét ∆MAB và ∆MAC, có:
AB = AC (do ∆ABC cân tại A),
AM là cạnh chung,
BM = CM (do M là trung điểm BC.
Do đó ∆MAB = ∆MAC (c.c.c).
Suy ra (cặp góc tương ứng).
Mà (hai góc kề bù).
Suy ra .
Do đó AM ⊥ BC tại M.
Mà M là trung điểm BC (giả thiết).
Suy ra AM là đường trung trực thứ ba của ∆ABC.
Vì vậy AM cũng đi qua giao điểm E của hai đường trung trực của AB và AC.
Do đó E ∈ AM.
Vậy ta chọn đáp án B.
Câu 9. Cho ∆ABC cân tại A, đường trung tuyến AM. Đường trung trực của AB cắt AM ở O. Biết OA = 4 cm. Tính OB và OC.
A. OB = OC = 2 cm;
B. OB = OC = 4 cm;
C. OB = OC = 8 cm;
D. OB = 2 cm; OC = 4 cm.
Đáp án đúng là: B
Xét ∆ABM và ∆ACM, có:
AM là cạnh chung,
AB = AC (∆ABC cân tại A),
BM = CM (AM là đường trung tuyến của ∆ABC)
Do đó ∆ABM = ∆ACM (c.c.c).
Suy ra (cặp góc tương ứng).
Ta có (hai góc kề bù).
Suy ra .
Vì vậy AM ⊥ BC.
Mà M là trung điểm BC (AM là đường trung tuyến của ∆ABC).
Do đó AM là đường trung trực của BC của ∆ABC.
Mà đường trung trực của AB cắt AM tại O
Khi đó O là giao điểm hai đường trung trực của tam giác nên cách đều các đỉnh
Suy ra OB = OC = OA = 4 cm.
Vậy ta chọn đáp án B.
Câu 10. Cho ∆ABC có O là giao điểm của ba đường trung trực của tam giác. Biết BO cũng là tia phân giác của . Khẳng định nào sau đây sai?
A. ∆BOA = ∆BOC;
B. ∆BAC cân tại A;
C. B thuộc đường trung trực của cạnh AC;
D. .
Đáp án đúng là: B
Vì O là giao điểm các đường trung trực của ∆ABC nên OA = OB = OC.
Do đó ∆OAB cân tại O và ∆OBC cân tại O.
Suy ra và (tính chất tam giác cân)
Mà (vì OB là tia phân giác của ) (1).
Ta suy ra (2).
∆ABO có: (3).
∆OBC có: (4).
Từ (1), (2), (3), (4), ta suy ra .
Do đó đáp án D đúng.
Xét ∆BOA và ∆BOC, có:
OB là cạnh chung.
(chứng minh trên).
OA = OC (chứng minh trên).
Do đó ∆BOA = ∆BOC (c.g.c)
Vì vậy đáp án A đúng.
Ta có ∆BOA = ∆BOC (chứng minh trên).
Suy ra AB = BC (cặp cạnh tương ứng).
Do đó ∆BAC cân tại B.
Vì vậy đáp án B sai.
Đến đây ta có thể chọn đáp án B.
Ta có BA = BC (chứng minh trên) và OA = OC (chứng minh trên).
Suy ra BO là đường trung trực của đoạn thẳng AC.
Vì vậy B thuộc đường trung trực của cạnh AC.
Do đó đáp án C đúng.
Vậy ta chọn đáp án B.
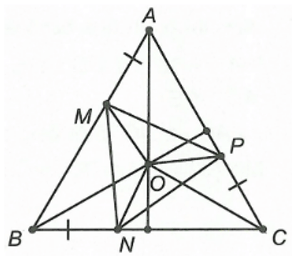
Câu 11. Cho ∆ABC đều. Trên các cạnh AB, BC, CA lấy theo thứ tự ba điểm M, N, P sao cho AM = BN = CP. Giao điểm của ba đường trung trực của ∆MNP là:
A. Điểm B;
B. Trung điểm của cạnh NP;
C. Trung điểm của cạnh MN;
D. Giao điểm của ba đường trung trực của ∆ABC.
Đáp án đúng là: D
Ta có AC = BC (do ∆ABC đều) và CP = BN (giả thiết).
Suy ra AC – CP = BC – BN.
Do đó AP = CN.
Xét ∆MAP và ∆PCN, có:
AM = CP (giả thiết).
(do ∆ABC đều).
AP = CN (chứng minh trên).
Do đó ∆MAP = ∆PCN (c.g.c)
Suy ra MP = PN (cặp cạnh tương ứng) (1).
Chứng minh tương tự, ta được MN = PN (2).
Từ (1), (2), ta suy ra MP = MN = PN.
Do đó ∆MNP đều.
Gọi O là giao điểm của các đường trung trực của ∆ABC
Khi đó OA = OB = OC (tính chất ba đường trung trực của tam giác)
Xét ∆BOA và ∆BOC có:
BA = BC (do ∆ABC đều),
BO là cạnh chung,
OA = OC (chứng minh trên)
Do đó ∆BOA = ∆BOC (c.c.c)
Suy ra (hai góc tương ứng)
Ta suy ra BO cũng là đường phân giác của ∆ABC.
Do đó .
Chứng minh tương tự, ta được:
và .
Xét ∆MAO và ∆NBO, có:
OA = OB (chứng minh trên).
(= 30°).
AM = BN (giả thiết).
Do đó ∆MAO = ∆NBO (c.g.c)
Suy ra MO = NO (cặp cạnh tương ứng) (3).
Chứng minh tương tự, ta được NO = PO (4).
Từ (3), (4), ta suy ra OM = ON = OP.
Do đó O là giao điểm của ba đường trung trực của ∆MNP.
Vì vậy giao điểm của ba đường trung trực của ∆MNP là giao điểm của ba đường trung trực của ∆ABC.
Vậy ta chọn đáp án D.
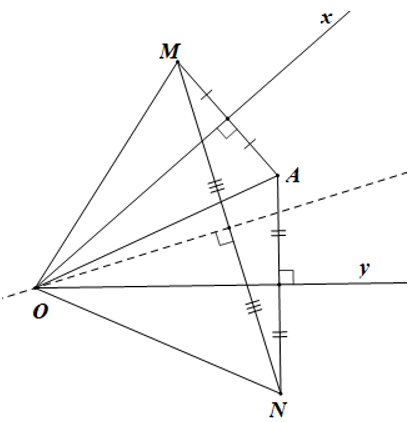
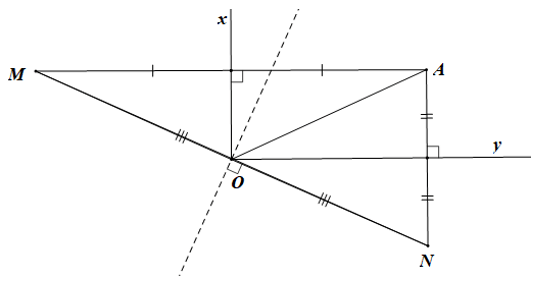
Câu 12. Cho , A là một điểm di động ở trong . Vẽ các điểm M và N sao cho Ox là đường trung trực của AM và Oy là đường trung trực của AN. Để O là trung điểm của MN của giá trị của α bằng:
A. 30°;
B. 60°;
C. 90°;
D. 120°.
Đáp án đúng là: C
∆AMN có Ox, Oy lần lượt là đường trung trực của các cạnh AM và AN.
Do đó O là giao điểm của ba đường trung trực của ∆AMN.
Suy ra đường trung trực của MN luôn đi qua điểm O cố định khi A di động (vì ba đường trung trực của một tam giác luôn đồng quy tại một điểm).
Vì Ox là đường trung trực của AM nên OA = OM.
Do đó ∆OMA cân tại O.
∆OMA cân tại O có Ox là đường trung trực.
Dễ dàng chứng minh được Ox cũng là tia phân giác của
Do đó .
Chứng minh tương tự, ta được .
Để O là trung điểm MN thì ba điểm O, M, N thẳng hàng.
Do đó .
Suy ra .
Hay
Khi đó .
Vì vậy α = 90°.
Vậy ta chọn đáp án C.
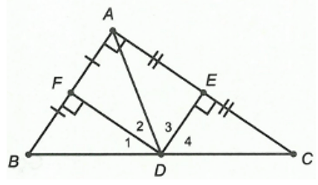
Câu 13. Cho ∆ABC vuông tại A. Gọi E, F lần lượt là trung điểm các cạnh AC, AB. Giao điểm của ba đường trung trực của tam giác ABC:
A. Nằm trong ∆ABC;
B. Nằm ngoài ∆ABC;
C. Là trung điểm của cạnh huyền BC;
D. Đáp án khác.
Đáp án đúng là: C
Gọi D là giao điểm của hai đường trung trực của các cạnh AC, AB.
Suy ra D cách đều các điểm A, B, C.
Do đó DA = DB = DC
Vì vậy ∆ACD cân tại D.
Xét ∆ADE và ∆CDE, có:
DE là cạnh chung.
.
AE = CE (do E là trung điểm AC).
Do đó ∆ADE = ∆CDE (c.g.c)
Suy ra (cặp góc tương ứng).
Chứng minh tương tự, ta được .
∆DEC vuông tại E: (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra .
Tương tự ta được .
Khi đó:
∆ABC vuông tại A: (trong tam giác vuông, hai góc nhọn phụ nhau)
Do đó
= 2.[180° – 90°] = 180°.
Suy ra ba điểm B, D, C thẳng hàng.
Ta có DB = DC (= DA).
Suy ra D là trung điểm của BC.
Vậy ta chọn đáp án C.
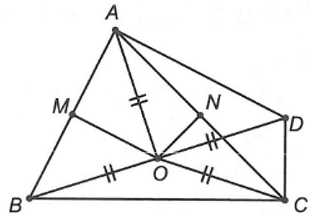
Câu 14. Cho ∆ABC có ba góc nhọn, O là giao điểm hai đường trung trực của AB và AC. Trên tia đối của tia OB, lấy điểm D sao cho OB = OD. Biết . Khẳng định nào sau đây đúng nhất?
A. ∆ABD vuông;
B. ∆CBD vuông;
C. ;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Vì O thuộc đường trung trực của cạnh AB nên OA = OB.
Suy ra ∆OAB cân tại O.
Do đó (tính chất tam giác cân)
∆OAB có: (tổng ba góc trong một tam giác)
Suy ra .
Do đó .
Chứng minh tương tự, ta được .
Do đó
(do hai góc kề bù).
= 90°.
Suy ra ∆ABD vuông tại A.
Do đó đáp án A đúng.
Chứng minh tương tự như trên, ta được ∆CBD vuông tại C.
Do đó đáp án B đúng.
∆ABD vuông tại A: (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra hay .
Tương tự, ta được .
Do đó
= 180° – 70° = 110°.
Suy ra .
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
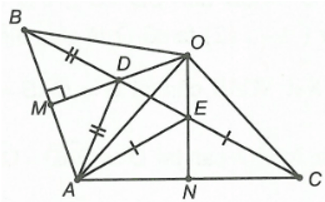
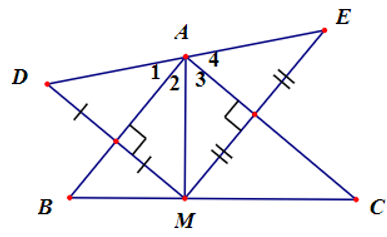
Câu 15. Cho ∆ABC vuông tại A. Trên cạnh BC lấy điểm M bất kì. Vẽ các điểm D và E sao cho AB là đường trung trực của MD và AC là đường trung trực của ME. Khẳng định nào sau đây đúng nhất?
A. Ba điểm D, A, E thẳng hàng;
B. DE ngắn nhất khi và chỉ khi AM ngắn nhất;
C. AM ngắn nhất khi và chỉ khi M là hình chiếu của A lên cạnh BC;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Vì AB là đường trung trực của MD.
Nên AD = AM và BD = BM (tính chất đường trung trực)
Suy ra ∆ADM cân tại A.
Xét DABD và DABM có:
AD = AM (chứng minh trên),
AB là cạnh chung,
BD = BM (chứng minh trên),
Do đó DABD = DABM (c.c.c)
Suy ra (hai góc tương ứng)
Vì vậy .
Chứng minh tương tự, ta được và .
Ta có .
Suy ra ba điểm D, A, E thẳng hàng.
Do đó đáp án A đúng.
Vì ba điểm D, A, E thẳng hàng
Nên DE = DA + AE = AM + AM = 2AM.
Suy ra DE ngắn nhất khi và chỉ khi AM ngắn nhất.
Do đó đáp án B đúng.
Vì M thuộc cạnh BC nên AM ngắn nhất khi và chỉ khi M là hình chiếu của A lên cạnh BC (quan hệ giữa đường vuông góc và đường xiên).
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.