30 câu Trắc nghiệm Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh (có đáp án 2024) – Toán 7 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 4.
Trắc nghiệm Toán 7 Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh
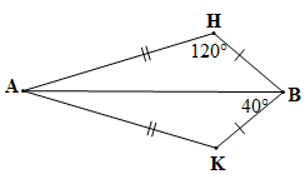
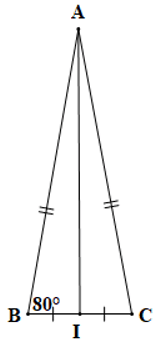
Câu 1. Cho hình vẽ bên dưới:
Số đo của ^KAB trong hình vẽ trên bằng:
A. 50°;
B. 40°;
C. 30°;
D. 20°.
Đáp án đúng là: D
Xét tam giác ABH và tam giác ABK có:
AH = AK, BH = BK, AB là cạnh chung
Suy ra ∆ABH = ∆ABK (c.c.c)
Do đó ˆH=ˆK (cặp góc tương ứng)
Mà ˆH=120° nên
Xét tam giác ABK có: (tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy số đo của bằng 20°.
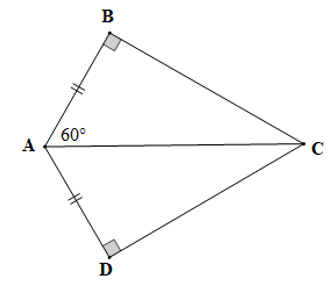
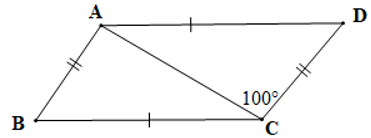
Câu 2. Cho hình vẽ bên dưới:
Biết AB=AD, . Số đo góc ACD là:
A. 20°;
B. 30°;
C. 40°;
D. 60°.
Đáp án đúng là: B
Xét ∆ABC và ∆ADC có:
AB = AD (giả thiết),
AC là cạnh chung
Do đó ∆ABC = ∆ADC (cạnh huyền – cạnh góc vuông)
Suy ra (cặp góc tương ứng)
Xét ∆ABC vuông tại B có: (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra
Mà (chứng minh trên)
Do đó
Vậy số đo góc ACD là 30°.
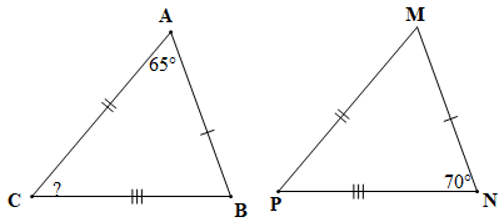
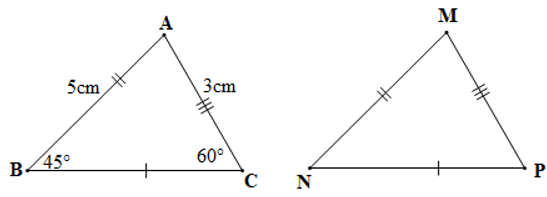
Câu 3. Cho hình vẽ bên dưới:
Số đo góc C và góc M lần lượt là:
A. 45° và 65°;
B. 65° và 45°;
C. 55° và 70°;
D. 70° và 55°.
Đáp án đúng là: A
Xét tam giác ABC và tam giác MNP có:
AB = MN, BC = NP, AC = MP (giả thiết)
Suy ra ∆ABC = ∆MNP (c.c.c)
Do đó (các cặp góc tương ứng)
Mà , nên
Xét tam giác ABC có: (tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy số đo góc C và góc M lần lượt là: 45° và 65°.
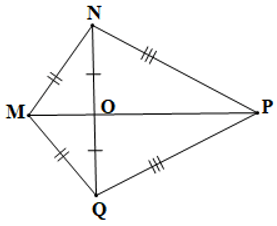
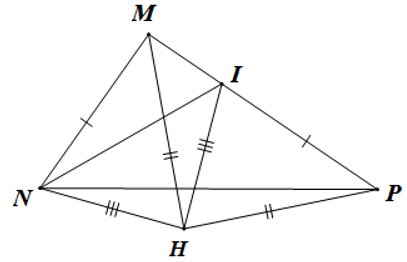
Câu 4. Cho hình vẽ bên dưới:
Số cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh là:
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án đúng là: C
+) Xét ∆MNP và ∆MQP có:
MN = MQ, NP = QP, MP là cạnh chung
Suy ra ∆MNP = ∆MQP (c.c.c)
+) Xét ∆NPO và ∆QPO có:
NP = QP, NO = QO, PO là cạnh chung
Suy ra ∆NPO = ∆QPO (c.c.c)
+) Xét ∆MNO và ∆MQO có:
MN = MQ, NO = QO, MO là cạnh chung
Suy ra ∆MNO = ∆MQO (c.c.c)
Vậy trong hình vẽ trên có 3 cặp tam giác bằng nhau theo trường hợp cạnh – cạnh – cạnh.
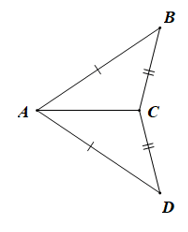
Câu 5. Cho hình vẽ bên dưới:
Khẳng định nào sau đây là sai?
A. và AD // BC;
B. và AD không song song với BC;
C. và AB // DC;
D. ∆ABC = ∆CDA.
Đáp án đúng là: B
• Xét ∆ABC và ∆ACD có:
AB = CD, BC = DA, AC là cạnh chung
Suy ra ∆ABC = ∆CDA (c.c.c)
Do đó phương án D là đúng.
• Vì ∆ABC = ∆CDA (chứng minh trên)
Nên (hai góc tương ứng)
Mà
Nên
Mặt khác: ∆ABC = ∆CDA (chứng minh trên)
Suy ra (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Do đó AD // BC (dấu hiệu nhận biết).
Vậy A là đúng
•Ta có (chứng minh trên)
Mà hai góc này ở vị trí so le trong
Do đó AB // DC (dấu hiệu nhận biết). Vậy C là đúng
Vậy ta chọn đáp án B.
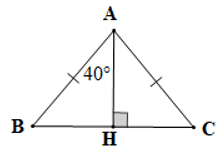
Câu 6. Cho hình vẽ sau:
Số đo của trong hình vẽ trên bằng:
A. 20°;
B. 40°;
C. 80°;
D. 120°.
Đáp án đúng là: C
Vì AHBCnên
Xét ∆ABH và ∆ACH có:
(chứng minh trên),
AB = AC (giả thiết),
AH là cạnh chung
Do đó ∆ABH = ∆ACH (cạnh huyền – cạnh góc vuông)
Suy ra (cặp góc tương ứng)
Mà nên
Ta có
Suy ra
Vậy số đo góc BAC là 80°.
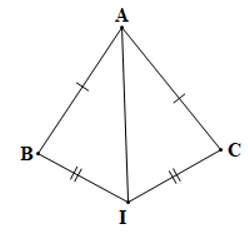
Câu 7. Xét bài toán “∆IAB và ∆IAC có AB = AC, IB = IC (điểm I nằm ngoài tam giác ABC). Chứng minh rằng .”
Cho các câu sau:
(1) “AB = AC (giả thiết),
IB = IC (giả thiết),
IA là cạnh chung”;
(2) “Suy ra ∆IAB = ∆IAC (c.c.c)”;
(3) “Do đó (hai góc tương ứng)”;
(4) “Xét ∆IAB và ∆IAC có:”.
Hãy sắp xếp một cách hợp lí các câu trên để giải bài toán.
A. (2), (4), (1); (3);
B. (4), (2), (1), (3);
C. (1), (2), (3), (4);
D. (4), (1), (2), (3).
Đáp án đúng là: D
Ta đi chứng minh như sau:
Xét ∆IAB và ∆IAC có:
AB = AC (giả thiết),
IB = IC (giả thiết),
IA là cạnh chung;
Suy ra ∆IAB = ∆IAC (c.c.c);
Do đó (hai góc tương ứng).
Vậy ta chọn phương án D.
Câu 8. Cho hình vẽ sau:
Khẳng định nào sau đây là đúng ?
A. ∆ABC = ∆ADC;
B. ∆ABC = ∆ACD;
C. ∆ACB = ∆ADC;
D. ∆BCA = ∆DAC.
Đáp án đúng là: A
Xét tam giác ABC và tam giác CDA có:
AB = AD, BC = DC, AC là cạnh chung
Suy ra ∆ABC = ∆ADC (c.c.c)
Vậy ∆ABC = ∆ADC hay ta có thể kí hiệu ∆ACB = ∆ACD hoặc ∆BCA = ∆DCA.
Do đó ta chọn phương án A.
Câu 9. Cho tam giác ABC có AB = AC, I là trung điểm của BC. Biết , số đo của là:
A. 40°;
B. 30°;
C. 20°;
D. 10°.
Đáp án đúng là: D
Xét tam giác ABI và tam giác ACI có:
AB = AC (giả thiết),
IB = IC (do I là trung điểm của BC),
AI là cạnh chung
Do đó ∆ABI = ∆ACI (c.c.c)
Suy ra (các cặp góc tương ứng)
Mà nên
Ta có: (hai góc kề bù)
Nên
Do đó tam giác ACI vuông tại I
Khi đó (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra
Vậy ta chọn phương án D.
Câu 10. Cho hình vẽ bên dưới:
Số đo góc M và độ dài cạnh MN lần lượt là:
A. MN = 5 cm;
B. MN = 3 cm;
C. MN = 5 cm;
D. MN = 3 cm.
Đáp án đúng là: C
Xét tam giác ABC và tam giác MNP có:
AB = MN, BC = NP, AC = MP (giả thiết)
Suy ra ∆ABC = ∆MNP (c.c.c)
Do đó MN = BA = 5 cm (hai cạnh tương ứng) và (hai góc tương ứng)
Xét tam giác BCA có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Do đó
Vậy và MN = 5 cm.
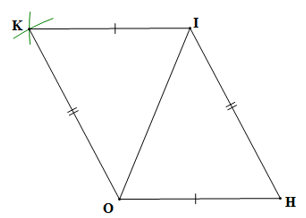
Câu 11. Cho tam giác IOH, vẽ cung tròn tâm I bán kính OH, vẽ cung tròn tâm O bán kính IH, hai cung tròn này cắt nhau tại K (K và H nằm khác phía so với đường thẳng IO). Khẳng định nào sau đây là đúng nhất?
A. HO // KI;
B. OK // IH;
C. Cả A và B đều sai;
D. Cả A và B đều đúng.
Đáp án đúng là: D
Xét ∆IOH và ∆IOK có:
KO = IH (K nằm trên cung tròn tâm O bán kính IH),
OH = IK (K nằm trên cung tròn tâm I bán kính OH),
IO là cạnh chung
Do đó ∆IOH = ∆OIK (c.c.c)
Suy ra (các cặp góc tương ứng)
Mà và ở vị trí so le trong của IK và OH nên IK // OH (dấu hiệu nhận biết)
và ở vị trí so le trong của KO và IH nên KO // IH (dấu hiệu nhận biết)
Vậy ta chọn phương án D.
Câu 12. Cho tam giác MNP có MN < MP. Lấy điểm I trên cạnh MP sao cho MN = PI. Gọi H là điểm sao cho HM = HP, HN = HI.
Khẳng định nào sau đây là đúng ?
A. ∆MNH = ∆PIH;
B. ∆MNH = ∆PHI;
C. ;
D. .
Đáp án đúng là: A
Xét ∆MNH và ∆PIH ta có:
HM = HP (giả thiết);
HN = HI (giả thiết);
MN = PI (giả thiết).
Do đó ∆MNH = ∆PIH (c.c.c)
Suy ra (các cặp góc tương ứng)
Vậy ta chọn phương án A.
Câu 13. Cho hai tam giác MNP và OHK có MN = OH, NP = HK. Điều kiện để ∆NMP = ∆HOK theo trường hợp cạnh – cạnh – cạnh là:
A. MP = OH;
B. MN = KH;
C. MP = OK;
D. Không có điều kiện nào thoả mãn.
Đáp án đúng là: C
Vì ∆NMP = ∆HOK theo trường hợp cạnh – cạnh – cạnh mà MN = OH, NP = HK
Nên điều kiện còn thiếu là MP = OK.
Vậy ta chọn phương án C.
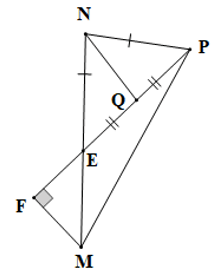
Câu 14. Cho tam giác NMP (NP < MN). Trên cạnh MN lấy điểm E sao cho NE = NP. Lấy Q là trung điểm của PE. Qua M kẻ đường thẳng vuông góc với PE tại F. Chọn khẳng định đúng:
A.
B. FM // NQ;
C. ∆ENQ = ∆PQN;
D. Cả A, B, C đều đúng.
Đáp án đúng là: B
• Xét ∆ENQ và ∆PQN có:
NE = NP (giả thiết),
QE = QP (do Q là trung điểm của PE),
NQ là cạnh chung
Suy ra ∆ENQ = ∆PNQ (c.c.c)
Do đó phương án C là sai.
• Vì ∆ENQ = ∆PNQ (chứng minh trên)
Suy ra (các cặp góc tương ứng)
Mà (hai góc kề bù)
Nên
Do đó NQ PE. Vậy đáp án A là sai
Mà FM PE (giả thiết), nên FM // NQ , vậy đáp án B là đúng
Vậy ta chọn phương án B.
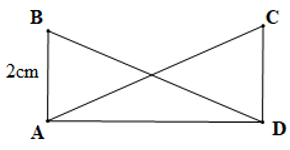
Câu 15. Cho hình vẽ:
Biết , AC = BD. Độ dài cạnh CD là:
A. 4 cm;
B. 5 cm;
C. 2 cm;
D. 3 cm.
Đáp án đúng là: C
Xét ∆ABD và ∆ACD có:
(giả thiết),
AC = BD (giả thiết),
AD là cạnh chung
Do đó ∆ABD = ∆DCA (cạnh huyền – cạnh góc vuông)
Suy ra AB = CD (cặp cạnh tương ứng)
Mà AB = 2 cm nên CD = 2 cm.
Vậy độ dài cạnh CD là 2 cm.