30 câu Trắc nghiệm Tam giác cân (có đáp án 2024) – Toán 7 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 7: Tam giác cân đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài ̃.
Trắc nghiệm Toán 7 Bài 7: Tam giác cân
Câu 1. Cho ∆PQR có ˆP=52°, . ∆PQR là tam giác gì?
A. Tam giác đều;
B. Tam giác vuông;
C. Tam giác cân;
D. Tam giác vuông cân.
Đáp án đúng là: C
∆PQR có: (định lí tổng ba góc của tam giác)
Suy ra .
Do đó ta có .
Suy ra ∆PQR cân tại R (dấu hiệu nhận biết)
Do đó đáp án C đúng.
Vì cả ba góc của ∆PQR đều không bằng nhau và không bằng 60° nên ∆PQR không thể là tam giác đều.
Do đó đáp án A sai.
Vì ∆PQR không có góc nào bằng 90° nên ∆PQR không thể là tam giác vuông.
Do đó đáp án B, D sai.
Vậy ta chọn đáp án C.
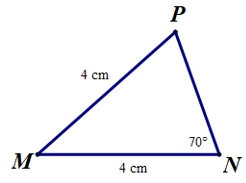
Câu 2. Tìm số đo ở hình bên:
A. ;
B. ;
C. ;
D. .
Đáp án đúng là: B
Vì MN = MP (= 4 cm).
Nên ∆MNP cân tại M.
Suy ra (tính chất tam giác cân)
∆MNP có: (định lí tổng ba góc trong tam giác)
Suy ra .
Khi đó ta có .
Vậy .
Do đó ta chọn đáp án B.
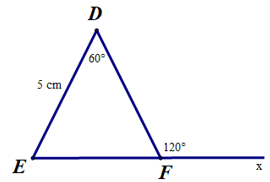
Câu 3. Cho hình bên dưới.
Độ dài cạnh EF bằng:
A. 2,5 cm;
B. 6 cm;
C. 5 cm;
D. 10 cm.
Đáp án đúng là: C
Ta có (hai góc kề bù).
Suy ra .
Do đó .
Suy ra ∆DEF cân tại D (dấu hiệu nhận biết)
Mà .
Suy ra ∆DEF là tam giác đều.
Suy ra EF = DF = DE = 5 cm.
Vậy ta chọn đáp án C.
Câu 4. Cho ∆ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD = CE. Hỏi ∆ADE là tam giác gì?
A. Tam giác cân;
B. Tam giác đều;
C. Tam giác vuông cân;
D. Tam giác vuông.
Đáp án đúng là: A
Vì ∆ABC cân tại A nên ta có (1).
Ta có (hai góc kề bù) (2).
Lại có (hai góc kề bù) (3).
Từ (1), (2), (3), ta suy ra .
Xét ∆ABD và ∆ACE, có:
AB = AC (∆ABC cân tại A),
(chứng minh trên),
BD = CE (giả thiết).
Do đó ∆ABD = ∆ACE (c.g.c).
Suy ra AD = AE (cặp cạnh tương ứng).
Do đó ∆ADE cân tại A (dấu hiệu nhận biết).
Vậy ta chọn đáp án A.
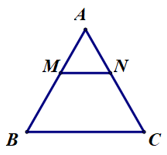
Câu 5. Cho ∆ABC đều. Lấy điểm M, N trên các cạnh AB, AC sao cho AM = AN. ∆AMN là tam giác gì?
A. Tam giác cân tại A;
B. Tam giác cân tại M;
C. Tam giác cân tại N;
D. Tam giác đều.
Đáp án đúng là: D
Vì AM = AN (giả thiết).
Nên ∆AMN là tam giác cân tại A.
Mà (do ∆ABC đều).
Suy ra ∆AMN là tam giác đều.
Vậy ta chọn đáp án D.
Câu 6. Hoàn thành định nghĩa của tam giác cân:
Tam giác cân là tam giác:
A. Có hai đường cao bằng nhau;
B. Có hai đường trung tuyến bằng nhau;
C. Có hai cạnh bằng nhau;
D. Có hai tia phân giác trong bằng nhau.
Đáp án đúng là: C
Định nghĩa: Tam giác cân là tam giác có hai cạnh bằng nhau.
Vậy ta chọn đáp án C.
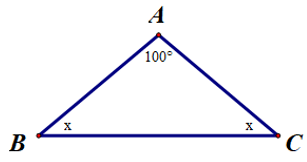
Câu 7. Cho ∆ABC như hình bên. Tìm số đo x:
A. x = 100°;
B. x = 80°;
C. x = 90°;
D. x = 40°.
Đáp án đúng là: D
∆ABC có .
Suy ra ∆ABC cân tại A (dấu hiệu nhận biết)
∆ABC có: (định lí tổng ba góc trong tam giác)
Suy ra 100° + x + x = 180°.
Do đó 2x = 180° – 100° = 80°.
Khi đó ta có x = 80° : 2 = 40°.
Vậy x = 40°.
Ta chọn đáp án D.
Câu 8. Khẳng định nào sau đây sai?
A. Tam giác cân có một góc bằng 60° là tam giác đều;
B. Tam giác vuông có một góc nhọn bằng 45° là tam giác vuông cân;
C. Trong một tam giác cân, hai góc ở đáy bằng nhau;
D. Tam giác cân không thể là tam giác tù.
Đáp án đúng là: D
Đáp án A, B, C đúng.
Đáp án D:
Tam giác tù là tam giác có một góc bất kỳ lớn hơn 90°.
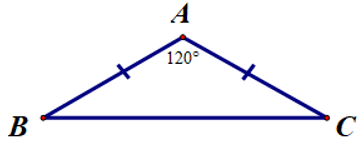
Giả sử ∆ABC cân tại A có (như hình bên).
Vì ∆ABC cân tại A nên ta có (tính chất tam giác cân)
∆ABC có: (định lí tổng ba góc trong tam giác)
Suy ra .
Do đó .
Khi đó .
Do đó ta có .
Ta thấy ∆ABC cân tại A có số đo các cạnh và các góc đều dương.
Mà .
Nên tam giác tù vẫn có thể là tam giác cân.
Do đó đáp án D sai.
Vậy ta chọn đáp án D.
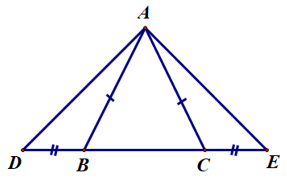
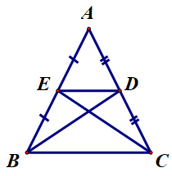
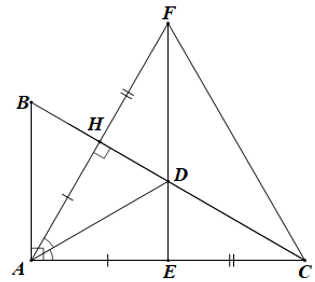
Câu 9. Cho tam giác ABC cân đỉnh A có các đường trung tuyến BD, CE. Tam giác nào dưới đây là tam giác cân?
A. ∆ABD;
B. ∆BCE;
C. ∆ADE;
D. ∆BDE.
Đáp án đúng là: C
∆ABC có BD là đường trung tuyến.
Suy ra D là trung điểm AC.
Do đó AD = DC = (1).
Chứng minh tương tự, ta được AE = EB = (2).
Vì ∆ABC cân tại A nên AB = AC (3).
Từ (1), (2), (3), ta suy ra AD = AE.
Do đó ∆ADE cân tại A (định nghĩa tam giác cân)
Suy ra đáp án C đúng.
Đáp án A, B, D sai vì các tam giác đó không có hai cạnh nào trong mỗi tam giác bằng nhau.
Vậy ta chọn đáp án C.
Câu 10. Cho ∆ABC có AB < AC. Ở phía ngoài ∆ABC, vẽ ∆ABD và ∆ACE vuông cân tại A. So sánh AD và AE.
A. AD < AE;
B. AD > AE;
C. AD = AE;
D. Không thể so sánh được.
Đáp án đúng là: A
Vì ∆ABD vuông cân tại A nên AB = AD (1).
Vì ∆ACE vuông cân tại A nên AC = AE (2).
Lại có AB < AC (giả thiết) (3).
Từ (1), (2), (3), ta suy ra AD < AE.
Vậy ta chọn đáp án A.
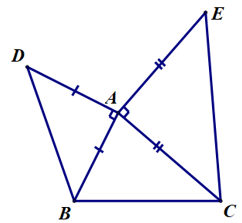
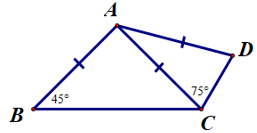
Câu 11. Cho hình vẽ bên.
Số đo bằng:
A. 45°;
B. 60°;
C. 90°;
D. 120°.
Đáp án đúng là: D
Ta có AB = AC nên ∆ABC cân tại A.
Do đó (tính chất tam giác cân)
∆ABC có: (định lí tổng ba góc trong tam giác)
Suy ra .
Ta có AC = AD nên ∆ACD cân tại A.
Do đó .
∆ACD có: (định lí tổng ba góc trong tam giác)
Suy ra .
Ta có .
Vậy ta chọn đáp án D.
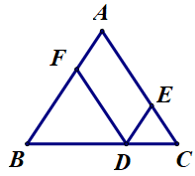
Câu 12. Cho ∆ABC cân tại A có cạnh bên bằng 3 cm. Gọi D là một điểm thuộc cạnh đáy BC. Qua D, kẻ các đường thẳng song song với các cạnh bên, chúng cắt AB và AC theo thứ tự tại F và E. Tổng DE + DF bằng:
A. 1,5 cm;
B. 3 cm;
C. 4,5 cm;
D. 6 cm.
Đáp án đúng là: B
Ta có DF // AC (giả thiết).
Do đó (hai góc đồng vị) .
Mà (do ∆ABC cân tại A).
Suy ra hay .
Do đó ∆BDF cân tại F (dấu hiệu nhận biết).
Suy ra BF = DF (1).
Ta có DF // AE và DE // AF (giả thiết).
Suy ra tứ giác AEDF là hình bình hành.
Suy ra DE = AF (2).
Từ (1), (2), ta suy ra DE + DF = AF + BF = AB = 3 cm.
Vậy ta chọn đáp án B.
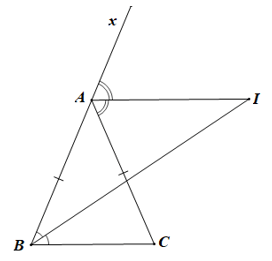
Câu 13. Cho ∆ABC cân tại A. Vẽ đường phân giác trong của và đường phân giác ngoài của , chúng cắt nhau tại I. Khẳng định nào sau đây đúng?
A. ∆ABI cân tại B;
B. AI // BC;
C. ∆ABI cân tại I;
D. ∆ABI vuông cân tại I.
Đáp án đúng là: B
Ta có ∆ABC cân tại A.
Suy ra .
∆ABC: (định lí tổng ba góc trong tam giác)
Suy ra .
Do đó (1).
Ta có: (hai góc kề bù).
Suy ra
Hay (do AI là phân giác của ).
Do đó (2).
Từ (1), (2), ta suy ra .
Mà hai góc này ở vị trí so le trong.
Ta suy ra AI // BC.
Do đó đáp án B đúng.
Vì AI // BC nên (hai góc so le trong).
Mà (do BI là phân giác của ).
Do đó .
Suy ra ∆ABI cân tại A (dấu hiệu nhận biết).
Do đó đáp án A, C, D sai.
Vậy ta chọn đáp án B.
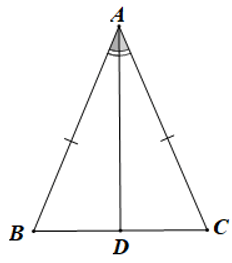
Câu 14. Cho ∆ABC cân tại A, tia phân giác trong của cắt BC tại D. Khẳng định nào dưới đây sai?
A. D là trung điểm BC;
B. ;
C. ∆ADB = ∆ADC;
D. .
Đáp án đúng là: D
Xét ∆ADB và ∆ADC, có:
AD là cạnh chung,
(do AD là tia phân giác của ),
AB = AC (do ∆ABC cân tại A).
Do đó ∆ADB = ∆ADC (c.c.c).
Suy ra đáp án C đúng.
Ta có ∆ADB = ∆ADC (chứng minh trên).
Suy ra BD = CD và (cặp cạnh và cặp góc tương ứng).
Vì BD = CD nên D là trung điểm BC.
Do đó đáp án A đúng.
Ta có (hai góc kề bù).
Suy ra .
Do đó AD ⊥ BC.
∆ABD vuông tại D: .
Mà (AD là phân giác của ).
Suy ra .
Do đó đáp án B đúng.
Ta có .
Suy ra .
Do đó .
Do đó đáp án D sai.
Vậy ta chọn đáp án D.
Câu 15. Cho ∆ABC vuông tại A có . Kẻ AH ⊥ BC tại H và tia phân giác AD của (D ∈ BC). Trên cạnh AC lấy điểm E sao cho AE = AH. Trên tia đối của tia HA lấy điểm F sao cho HF = EC. Khẳng định nào sau đây đúng nhất?
A. ∆ADH = ∆ADE;
B. DE ⊥ AC;
C. ∆ACF đều;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Ta xét từng đáp án:
Đáp án A:
Xét ∆ADH và ∆ADE, có:
AH = AE (giả thiết).
(do AD là phân giác của ).
AD là cạnh chung.
Do đó ∆ADH = ∆ADE (c.g.c)
Suy ra đáp án A đúng.
Đáp án B:
∆ADH = ∆ADE (chứng minh trên).
Suy ra (cặp góc tương ứng).
Mà (do AH ⊥ HD).
Do đó .
Khi đó ta có DE ⊥ AE hay DE ⊥ AC.
Do đó đáp án B đúng.
Đáp án C:
Ta có AH = AE (giả thiết) và HF = EC (giả thiết).
Suy ra AH + HF = AE + EC.
Do đó AF = AC.
Khi đó ta có ∆ACF cân tại A (1).
Vì ∆AHC vuông tại H nên .
Do đó (2).
Từ (1), (2), ta suy ra ∆ACF là tam giác đều.
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.