30 câu Trắc nghiệm Hai tam giác bằng nhau (có đáp án 2024) – Toán 7 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 3: Hai tam giác bằng nhau đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 3.
Trắc nghiệm Toán 7 Bài 3: Hai tam giác bằng nhau
Câu 1. Cho ∆ABC = ∆DEF có AC = 6,2 cm, BC = 8,7 cm, DE = 12,5cm. Chu vi tam giác DEF là:
A. 28,4 cm;
B. 28,7 cm;
C. 24,8cm;
D. 27,4 cm.
Đáp án đúng là: D
Vì ∆ABC = ∆DEF nên AC = DF, BC = EF (các cặp cạnh tương ứng)
Do đó DF = 6,2 cm, EF = 8,7 cm.
Khi đó chu vi của tam giác DEF là:
DE + DF + EF = 12,5 + 6,2 + 8,7 = 27,4 (cm)
Vậy chu vi của tam giác DEF bằng 27,4 cm.
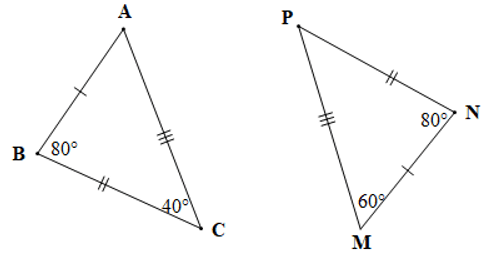
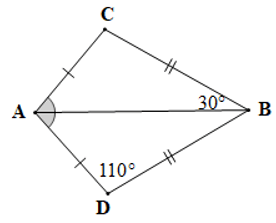
Câu 2. Cho hai tam giác ABC và MNP như hình vẽ dưới đây:
Khẳng định nào sau đây là đúng?
A. ∆ABC = ∆MNP;
B. ∆ABC = ∆MPN;
C. ∆ABC = ∆NMP;
D. ∆ABC = ∆NPM.
Đáp án đúng là: A
Xét tam giác ABC ta có: ˆA+ˆB+ˆC=180°(định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Xét tam giác MNP ta có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Khi đó: tam giác ABC và tam giác MNP có:
+) AB = NM, BC = NP, AC = MP;
+)
Do đó hai tam giác ABC và MNP bằng nhau và được kí hiệu là DABC = DMNP.
Vậy ta chọn phương án A.
Câu 3. Cho ∆MNP = ∆DEG. Biết MN = 3 cm, .Độ dài cạnh DE và số đo góc P là:
A.DE = 3 cm và
B. DE = 4 cm và
C.DE = 3 cm và
D.DE = 4 cm và
Đáp án đúng là: A
- Vì ∆MNP = ∆DEG nên ta có:
+) MN = DE (hai cạnh tương ứng)
Mà MN = 3 cm nên DE = 3cm;
+) (hai góc tương ứng)
Mà nên
- Xét tam giác MNP có (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy DE = 3 cm và
Câu 4. Cho tam giác ABC và điểm M thuộc cạnh BC thỏa mãn ∆ABM = ∆ACM. Biết BC = 6 cm, số đo cạnh BM là:
A. 6 cm;
B. 5 cm;
C. 4 cm;
D. 3 cm.
Đáp án đúng là: D
Vì ∆ABM = ∆ACM nên MB = MC (cặp cạnh tương ứng)
Vì điểm M thuộc cạnh BC nên MB + MC = BC
Mà BC = 6 cm
Suy ra BM + BM = 6
Hay 2.BM = 6
Do đó BM = 6 : 2 = 3
Vậy độ dài cạnh BM là 3 cm.
Câu 5. Cho ∆ABC = ∆DEG biết . Số đo góc G là:
A. 50°;
B. 60°;
C. 70°;
D. 80°.
Đáp án đúng là: D
Vì ∆ABC = ∆DEG nên ta có:
(các cặp góc tương ứng)
Mà nên
Xét tam giác DEG ta có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Vậy số đo góc G bằng 80°.
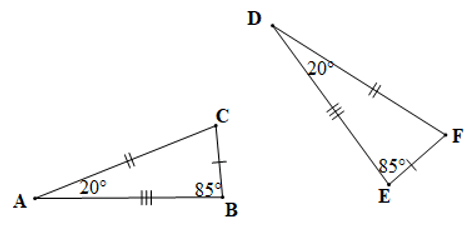
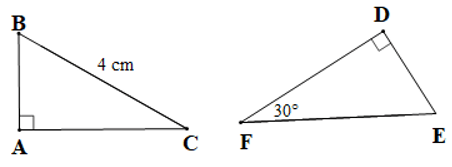
Câu 6. Cho hai tam giác ABC và DEF như hình vẽ dưới đây:
Khẳng định nào sau đây là đúng?
A. ABC = DEF;
B. ABC = DFE;
C. ABC = EDF;
D. ABC = FDE.
Đáp án đúng là: A
Xét tam giác FDE có (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Xét tam giác BCA ta cũng có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Xét tam giác FDE và tam giác BCA có:
+) AB = DE, AC = DF, BC = EF
+)
Do đó ABC = DEF.
Vậy ta chọn phương án A.
Câu 7. Cho hai tam giác ABC và NPM có: AB = MN, AC = MP, BC = PN, , ,. Cách viết nào dưới đây là đúng?
A. ABC = ∆NPM;
B. ∆ABC = ∆NMP;
C. ∆ABC = ∆MNP;
D. ∆ABC = ∆PNM.
Đáp án đúng là: C
Xét ∆ABC và ∆MNP có:
+) AB = MN, AC = MP, BC = NP;
+) , , .
Do đó tam giác ABC và tam giác MNP bằng nhau và kí hiệu bằng nhau của hai tam giác đó là: ∆ABC = ∆MNP.
Vậy ta chọn phương án C.
Câu 8. Cho biết ∆ABC = ∆XYZ, AB = 4 cm, AC = 3 cm, BC = 6 cm. Độ dài cạnh XY là:
A. 3 cm;
B. 4 cm;
C. 5 cm;
D. 6 cm.
Đáp án đúng là: B
Vì ∆ABC = ∆XYZ nên ta có:
AB = XY (hai cạnh tương ứng)
Mà AB = 4 cm nên XY = 4cm
Vậy độ dài cạnh XY là 4 cm.
Câu 9. Cho ∆KQR = ∆MNP biết . Số đo góc R là:
A. 68°;
B. 52°;
C. 60°;
D. 50°.
Đáp án đúng là: C
Xét tam giác MNP có (tổng ba góc trong một tam giác)
Suy ra
Hay
Vì ∆KQR = ∆MNP nên ta có (hai góc tương ứng)
Do đó
Vậy số đo góc R bằng 60°.
Câu 10. Cho ∆ABC = ∆HIK. Khẳng định nào sau đây là đúng?
A.
B.
C. AB = HK;
D. BC = HK.
Đáp án đúng là: B
Vì ∆ABC = ∆HIK nên ta có:
+) (hai góc tương ứng). Do đó A là sai.
+) (hai góc tương ứng).
Hay . Do đó B là đúng.
+) AB = HI, BC = IK (các cặp cạnh tương ứng). Do đó C và D là sai.
Vậy ta chọn phương án B.
Câu 11. Cho ∆ABC = ∆HIK. Biết . Khẳng định nào sau đây là đúng?
A.
B.
C.
D.
Đáp án đúng là: C
Xét tam giác ABC có (tổng ba góc trong một tam giác)
Suy ra
Hay
Vì ∆ABC = ∆HIK nên ta có (hai góc tương ứng)
Do đó
Mà nên
Vì 85° > 65° > 30°
Do đó
Vậy ta chọn phương án C.
Câu 12. Cho tam giác DEG (không có hai góc nào bằng nhau, không có hai cạnh nào bằng nhau) bằng tam giác có ba đỉnh I, H, K. Biết . Kí hiệu về sự bằng nhau của hai tam giác là:
A. ∆DEG = ∆IHK;
B. ∆DEG = ∆HIK;
C. ∆DEG = ∆KIH;
D. ∆DEG = ∆KHI.
Đáp án đúng là: D
Vì tam giác DEG và tam giác có ba đỉnh I, H, K bằng nhau, lại có .
Do đó, nếu hai tam giác đó bằng nhau thì:
+ Đỉnh D của tam giác DEG tương ứng với đỉnh K của tam giác IHK;
+ Đỉnh G của tam giác DEG tương ứng với đỉnh I của tam giác IHK.
Khi đó đỉnh E của tam giác ABC tương ứng với đỉnh H của tam giác IHK.
Vậy kí hiệu bằng nhau của hai tam giác này là: ∆DEG = ∆KHI.
Câu 13. Cho ∆ABC = ∆PQR, biết BC = 4 cm. Cạnh nào của tam giác PQR có độ dài bằng 4 cm?
A. QP;
B. QR;
C. PR;
D. Không có cạnh nào.
Đáp án đúng là: B
Vì ∆ABC = ∆PQR nên BC = QR (hai cạnh tương ứng)
Do đó BC = QR= 4 cm.
Vậy cạnh QR của tam giác PQR có độ dài bằng 4 cm.
Câu 14. Trong hình vẽ sau:
Biết AB là tia phân giác của và . Hãy chọn khẳng định đúng trong các khẳng định sau:
A. ∆ABC = ∆ADB;
B. ∆ABC = ∆BAD;
C. ∆BAC = ∆ABD;
D. ∆CAB = ∆DAB.
Đáp án đúng là: D
Vì AB là tia phân giác của nên ta có (tính chất tia phân giác của một góc)
Mà do đó
Xét tam giác ABC ta có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Xét tam giác ABD ta có: (định lí tổng ba góc trong một tam giác)
Suy ra
Hay
Khi đó: tam giác ABC và tam giác ABD có:
+) AC = AD, BC = BD, AB là cạnh chung;
+)
Do đó hai tam giác ABC và tam giác ABD bằng nhau và được kí hiệu là:
∆ABC = ∆ABD hoặc có thể kí hiệu là: ∆CAB = ∆DAB.
Vậy ta chọn phương án D.
Câu 15. Trong hình vẽ sau:
Biết ∆ABC = ∆DEF, BC = 4 cm, . Độ dài cạnh FE và số đo góc B là:
A.FE = 4 cm và
B. FE = 4 cm và
C.FE = 5 cm và
D.FE = 5 cm và
Đáp án đúng là: B
- Vì ∆ABC = ∆DEF nên ta có:
+) BC = FE (hai cạnh tương ứng)
Mà BC = 4 cm nên FE = 4cm;
+) (hai góc tương ứng)
Mà nên
Vì tam giác ABC vuông tại A nên(trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra
Hay
Vậy FE = 4 cm và