30 câu Trắc nghiệm Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh (có đáp án 2024) – Toán 7 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 5.
Trắc nghiệm Toán 7 Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh
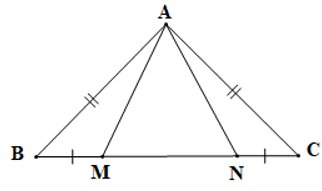
Câu 1. Cho hình vẽ dưới đây:
Biết AB = AC, BM = NC, ^ABC=^ACB. Xét các khẳng định sau:
(1) ∆ABM = ∆ACN;
(2) ∆ABN = ∆ACM.
Chọn câu đúng:
A. Chỉ có (1) đúng;
B. Chỉ có (2) đúng;
C. Cả (1) và (2) đều sai;
D. Cả (1) và (2) đều đúng.
Đáp án đúng là: D
+ Xét ∆ABM và ∆ACN có:
AB = AC (giả thiết),
^ABM=^ACN (giả thiết),
BM = CN (giả thiết)
Do đó ∆ABM = ∆ACN (c.g.c)
+ Vì BN = BM + MN, CM = CN + MN
Mà BM = CN (giả thiết) nên BN = CM.
Xét ∆ABN và ∆ACM có:
AB = AC (giả thiết),
^ABN=^ACM (giả thiết),
BN = CM (chứng minh trên)
Do đó ∆ABN = ∆ACM (c.g.c)
Vậy cả phương án A và B đều đúng, ta chọn phương án D.
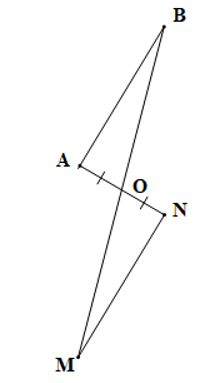
Câu 2. Cho hình vẽ sau:
Điều kiện để ∆ABO = ∆NMO theo trường hợp cạnh – góc – cạnh là:
A. ^ABO=^NMO;
B. AB = OM;
C. OB = OM;
D. AB = MN.
Đáp án đúng là: C
Vì ∆ABO = ∆NMO theo trường hợp cạnh – góc – cạnh nên điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà ^AOB=^MON (hai góc đối đỉnh)
Góc AOB xen kẽ giữa hai cạnh OA và OB, góc MON xen kẽ giữa hai cạnh OM và ON.
Mà OA = ON nên điều kiện còn thiếu trong trường hợp này là điều kiện về cạnh, đó là OB = OM.
Vậy ta chọn phương án C.
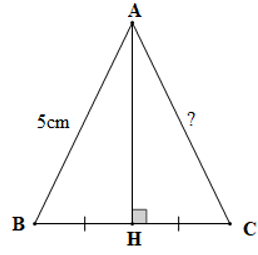
Câu 3. Cho hình vẽ sau:
Độ dài cạnh AC là:
A. 3 cm;
B. 4 cm;
C. 5 cm;
D. 6 cm.
Đáp án đúng là: C
Xét tam giác ABH và tam giác ACH có:
AH là cạnh chung,
^AHB=^CHA=90° (giả thiết),
BH = CH (giả thiết),
Do đó ∆ABH = ∆ACH (c.g.c)
Suy ra AB = AC (hai cạnh tương ứng)
Mà AB = 5 cm nên AC = 5 cm.
Vậy độ dài cạnh AC là 5 cm.
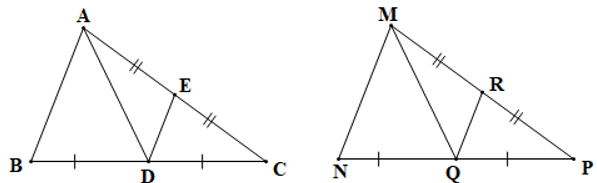
Câu 4. Cho ∆ABC = ∆MNP. D,E, Q, R lần lượt là trung điểm của BC,CA, NP,PM. Khẳng định nào sau đây là sai?
A. ∆ABD = ∆MNQ;
B. ∆CDE = ∆PQR;
C. ∆ADC = ∆MQP;
D. ∆ACD = ∆MQP.
Đáp án đúng là: D
+) Vì ∆ABC = ∆MNP (giả thiết)
Nên ta có:
• AC = MP, BC = NP, AB = MN (các cặp cạnh tương ứng)
• (các cặp góc tương ứng)
Mà , ,,
(E, D, R, Q lần lượt là trung điểm của CA, CB, MP, NP)
Suy ra AE = EC = MR = RP, BD = DC = NQ = QP
+) Xét ∆ABD và ∆MNQ có:
AB = MN (chứng minh trên),
(chứng minh trên),
BD = NQ (chứng minh trên)
Do đó ∆ABD = ∆MNQ (c.g.c)
Vậy A là đúng.
+) Xét ∆CDE và ∆PQR có:
CD = PQ (chứng minh trên),
(chứng minh trên),
CE = PR (chứng minh trên)
Do đó ∆CDE = ∆PQR (c.g.c)
Vậy B là đúng.
+) Xét ∆ADC và ∆MQP có:
AC = PM (chứng minh trên),
(chứng minh trên),
CD = PQ (chứng minh trên)
Do đó ∆ADC = ∆MQP(c.g.c).
Vậy C là đúng, D là sai.
Ta chọn phương án D.
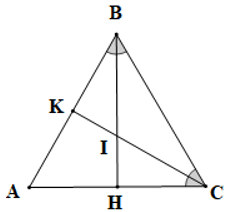
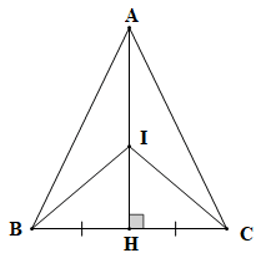
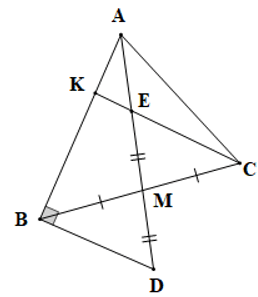
Câu 5. Cho tam giác ABC có AB = AC = BC, phân giác BH và CK cắt nhau tại I. Cho các phát biểu sau:
(I) CK AB;
(II) BH CK ;
(III) BH AC;
(IV)
Số phát biểu đúng là:
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án đúng là: C
Tam giác ABC có AB = AC = BC (giả thiết) nên là tam giác đều
Do đó
Vì CK là tia phân giác của (giả thiết)
Nên (tính chất tia phân giác) (1)
Xét ∆ACK và ∆BCK có:
AC = BC (giả thiết),
(chứng minh trên),
CK là cạnh chung.
Do đó ∆ACK = ∆BCK (c.g.c)
Suy ra (hai góc tương ứng)
Mà (tính chất hai góc kề bù)
Nên
Do đó CK AB. Nên (I) là phát biểu đúng.
Mà BH là tia phân giác của (giả thiết)
Nên (tính chất tia phân giác) (2)
Xét ∆ABH và ∆CBH có:
AB = BC (giả thiết),
(chứng minh trên),
BH là cạnh chung
Do đó ∆ABH = ∆CBH (c.g.c)
Suy ra (hai góc tương ứng)
Mà (tính chất hai góc kề bù)
Nên
Do đó BH AC.
Nên (II) là phát biểu sai và (III) là phát biểu đúng.
Từ (1) và (2) suy ra .
Hay
Nên (IV) là phát biểu đúng.
Vậy có 3 phát biểu đúng, ta chọn phương án C.
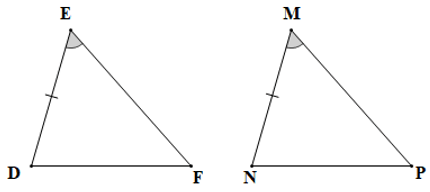
Câu 6. Cho tam giác MNP và tam giác DEF có: MN = DE, . Điều kiện để ∆DEF = ∆NMP theo trường hợp cạnh – góc – cạnh là:
A. DF = NP;
B. FE = MP;
C. ;
D. .
Đáp án đúng là: B
Vì ∆DEF = ∆NMP theo trường hợp cạnh – góc – cạnh nên điều kiện về cặp góc bằng nhau của hai tam giác là góc xen kẽ giữa hai cạnh.
Mà là góc xen kẽ giữa hai cạnh ED và EF, là góc xen kẽ giữa hai cạnh MN và MP.
Lại có ED = MN
Do đó điều kiện còn lại là điều kiện về cạnh, đó là FE = MP.
Ta chọn phương án B.
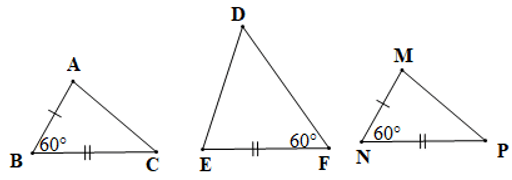
Câu 7. Cho hình vẽ sau:
Khẳng định nào sau đây là đúng?
A. ∆ABC = ∆MNP;
B. ∆ABC = ∆DEF;
C. ∆MNP = ∆DEF;
D. ∆ABC = ∆MNP = ∆DEF.
Đáp án đúng là: A
Xét ∆ABC và ∆MNP có:
BA = MN (giả thiết),
(giả thiết),
CB = NP (giả thiết)
Do đó ∆ABC = ∆MNP (c.g.c)
Vậy ta chọn phương án A.
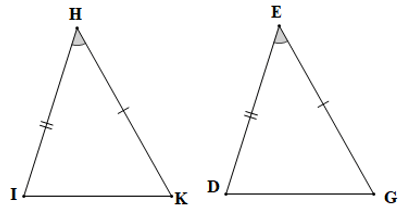
Câu 8. Cho tam giác HIK và tam giác DEG có IH = DE, ,HK = EG. Phát biểu nào sau đây là đúng:
A. ∆HIK = ∆EDG;
B. ∆HIK = ∆DGE;
C. ∆HIK = ∆DEG;
D. ∆HIK = ∆EGD.
Đáp án đúng là: A
Xét ∆HIK và ∆GED có:
IH = DE (giả thiết),
(giả thiết),
HK = EG (giả thiết)
Do đó ∆HIK = ∆EDG (c.g.c)
Vậy ta chọn phương án A.
Câu 9. Cho ∆ABC và ∆MNP có AB = NM, , AC = PM. Biết , số đo góc P là:
A. 45°;
B. 50°;
C. 65°;
D. 70°.
Đáp án đúng là: C
Xét ∆ABC và ∆MNP có:
AB = NM (giả thiết),
(giả thiết),
AC = PM (giả thiết),
Do đó ∆ABC = ∆MNP (c.g.c)
Suy ra (hai góc tương ứng)
Xét ∆MNP có (định lí tổng ba góc của tam giác)
Suy ra
Do đó
Vậy .
Câu 10. Qua trung điểm H của đoạn thẳng BC, kẻ đường thẳng vuông góc với BC, trên đường thẳng vuông góc đó lấy hai điểm A và I. Nối CA, AB, IB, IC. Phát biểu nào sau đây là đúng nhất:
A. ∆ABH = ∆ACH;
B. ∆IBH = ∆ICH;
C. ∆BAI = ∆CAI;
D. Cả A, B, C đều đúng.
Đáp án đúng là: D
Vì A nằm trên đường thẳng vuông góc với CB tại H nên ta có:
Vì I nằm trên đường thẳng vuông góc với CB tại H nên ta có:
+) Xét ∆ABH và ∆ACH có:
(chứng minh trên),
AH là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ∆ABH = ∆ACH (hai cạnh góc vuông)
Do đó đáp án A đúng
Vì ∆ABH = ∆ACH (chứng minh trên)
Suy ra AB = AC (hai cạnh tương ứng) và (hai góc tương ứng)
+) Xét tam giác HCI và tam giác HBI có:
(chứng minh trên),
HI là cạnh chung,
BH = CH (do H là trung điểm của CB),
Suy ra ∆ICH = ∆IBH (hai cạnh góc vuông)
Do đó đáp án B đúng
+) Xét tam giác BAI và tam giác CAI có:
AB = AC (chứng minh trên),
(do ),
AI là cạnh chung
Suy ra ∆BAI = ∆CAI (c.g.c)
Do đó đáp án C đúng.
Vậy ta chọn đáp án D.
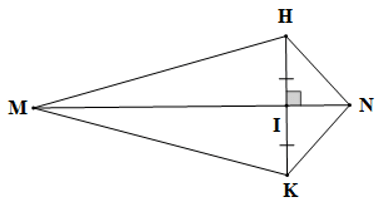
Câu 11. Cho hình vẽ dưới đây:
Số cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh là:
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án đúng là: C
+ Xét ∆MHI và ∆MKI có:
, HI = KI, MI là cạnh chung
Do đó ∆MHI = ∆MKI (c.g.c)
+ Xét ∆HIN và ∆KIN có:
, HI = KI, IN là cạnh chung
Do đó ∆HIN = ∆KIN (c.g.c)
Suy ra (hai góc tương ứng) và HN = KN (hai cạnh tương ứng)
+ Xét ∆MHN và ∆MKN có:
HN = KN (chứng minh trên);
(do )
MN là cạnh chung
Do đó ∆MHN = ∆MKN (c.g.c)
Vậy có 3 cặp tam giác bằng nhau theo trường hợp cạnh – góc – cạnh.
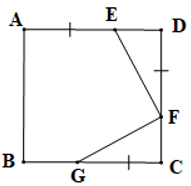
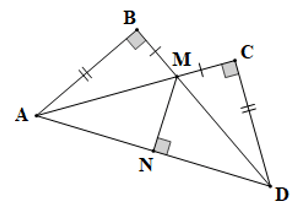
Câu 12. Cho hình vuông ABCD, trên cạnh AD lấy điểm E, trên cạnh DC lấy điểm F và trên cạnh BC lấy điểm G sao cho AE = DF = CG. Số đo góc GFE là:
A. 45°;
B. 90°;
C. 60°;
D. 100°.
Đáp án đúng là: B
Vì ABCD là hình vuông (giả thiết) nên AD = CD (tính chất hình vuông)
Do đó AE + ED = CF + FD
Mà AE = FD (giả thiết) nên ED = CF.
Xét ∆FED và ∆GFC có:
FD = CG (giả thiết),
(, tính chất hình vuông),
ED = CF (chứng minh trên)
Do đó ∆FED = ∆GFC (hai cạnh góc vuông)
Suy ra (hai góc tương ứng)
Mà (trong tam giác FDE vuông tại D, hai góc nhọn phụ nhau)
Do đó
Mặt khác
Suy ra
Vậy
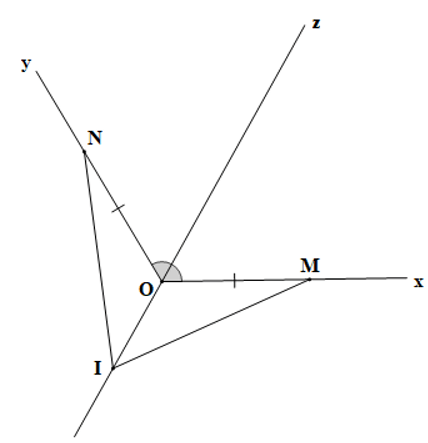
Câu 13. Cho góc xOy tù , gọi Oz là tia phân giác của góc xOy. Trên tia Ox lấy điểm M, trên tia Oy lấy điểm N sao cho OM = ON. Trên tia đối của tia Oz lấy điểm I tuỳ ý. Chọn phát biểu đúng nhất:
A. ;
B. IM = IN;
C. IO là tia phân giác của ;
D. Cả A, B, C đểu đúng.
Đáp án đúng là: D
Vì tia Oz là tia phân giác của góc xOy nên (tính chất tia phân giác của một góc)
Mà (tính chất hai góc kề bù) và (tính chất hai góc kề bù)
Do đó hay
Xét ∆MOI và ∆NOI có:
OM = ON (giả thiết),
(chứng minh trên),
OI là cạnh chung
Do đó ∆MOI = ∆NOI (c.g.c)
Suy ra IM = IN (hai cạnh tương ứng) và (hai góc tương ứng)
Vì nên tia IO là tia phân giác của
Vậy ta chọn phương án D.
Câu 14. Cho hình vẽ sau:
Biết . Số đo góc AMN là:
A. 100°;
B. 80°;
C. 65°;
D. 50°.
Đáp án đúng là: D
Xét ∆ABM và ∆DCM có:
(= 90°),
BM = CM (giả thiết),
AB = CD (giả thiết)
Do đó ∆ABM = ∆DCM (hai cạnh góc vuông)
Suy ra MA = MD (hai cạnh tương ứng)
Xét ∆ANM và ∆DNM có:
AM = DM (chứng minh trên),
(= 90°),
MN là cạnh chung
Do đó ∆ANM = ∆DNM (cạnh huyền – cạnh góc vuông)
Suy ra (hai góc tương ứng)
Mà (giả thiết)
Nên .
Vậy đo góc AMN là 50°.
Câu 15. Cho hình vẽ sau:
Số đo góc AKC là:
A. 100°;
B. 90°;
C. 80°;
D. 70°.
Đáp án đúng là: B
Xét ∆EMC và ∆DMB có:
ME = MD (giả thiết),
(hai góc đối đỉnh),
MB = MC (giả thiết)
Do đó ∆EMC = ∆DMB (c.g.c)
Suy ra (hai góc tương ứng)
Lại có (hai góc đối đỉnh)
Nên
Mà hai góc và ở vị trí đồng vị
Suy ra KE // BD
Do đó (hai góc đồng vị)
Mà nên
Vậy .