30 câu Trắc nghiệm Phép nhân đa thức một biến (có đáp án 2024) – Toán 7 Cánh diều
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 4: Phép nhân đa thức một biến đầy đủ các mức độ sách Cánh diều giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 4.
Trắc nghiệm Toán 7 Bài 4: Phép nhân đa thức một biến
Câu 1. Biết 5(2x − 1) − 4(8 − 3x) = 84. Giá trị của x là:
A. x = 4;
B. x = 4,5;
C. x = 5;
D. x = 5,5.
Đáp án đúng là: D
Ta có: 5(2x − 1) − 4(8 − 3x) = 84
Suy ra 10x − 5 − 32 + 12x = 84
10x + 12x = 84 + 5 + 32
22x = 121
x = 5,5
Vậy x = 5,5.
Ta chọn phương án D.
Câu 2. Tìm hệ số cao nhất của đa thức P(x) = (2x – 1)(3x2 – 7x + 5).
A. –5;
B. 17;
C. –17;
D. 6.
Đáp án đúng là: D
Ta có (2x – 1)(3x2 – 7x + 5)
= 2x.3x2 + 2x.(–7x) + 2x.5 – 1.3x2 – 1.(–7x) – 1.5
= 6x3 – 14x2 + 10x – 3x2 + 7x – 5
= 6x3 – 17x2 + 17x – 5
Vậy hệ số cao nhất của P(x) là 6.
Câu 3. Rút gọn và tính giá trị của biểu thức: P(x) = 5x2 – [4x2 – 3x(x – 2)] với x = 2.
A. P(x) = 4x2 – 6x; P(2) = 2;
B. P(x) = 4x2 + 6x; P(2) = 4;
C. P(x) = 4x2 – 6x; P(2) = 4;
D. P(x) = 4x2 + 6x; P(2) = 4;
Đáp án đúng là: C
Ta có P(x) = 5x2 – [4x2 – 3x(x – 2)]
= 5x2 – (4x2 – 3x2 + 6x)
= 5x2 – (x2 + 6x)
= 5x2 – x2 – 6x
= 4x2 – 6x
Thay x = 2 vào P(x) = 4x2 – 6x ta được:
P(2) = 4. 22 – 6. 2
= 4.4 – 6. 2
= 16 – 12
= 4.
Vậy ta chọn phương án C.
Câu 4. Cho hình chữ nhật có chiều dài lớn hơn chiều rộng là 5 đơn vị. Biểu thức tính diện tích hình chữ nhật là:
A. S = x2 + 5x;
B. S = 2(x2 + 5x);
C. S = 2x + 5;
D. S = x2 – 5x.
Đáp án đúng là: A
Gọi x (x > 0) là chiều rộng của hình chữ nhật
Theo giả thiết ta có chiều dài hình chữ nhật là x + 5
Diện tích hình chữ nhật là:
S = x(x + 5) = x2 + 5x (đvdt)
Ta chọn phương án A.
Câu 5. Cho biểu thức P(x) = x2(x2 + x + 1) – 3x(x – a) + 4. Tìm a sao cho tổng các hệ số của đa thức bằng –2.
A. –1;
B. 1;
C. –2;
D. 2.
Đáp án đúng là: C
P(x) = x2(x2 + x + 1) – 3x(x – a) + 4
= x4 + x3 + x2 – 3x2 + 3ax + 4
= x4 + x3 – 2x2 + 3ax + 4
Ta có:
Hệ số của lũy thừa bậc 4 của x là 1;
Hệ số của lũy thừa bậc 3 của x là 1;
Hệ số của lũy thừa bậc 2 của x là –2;
Hệ số của lũy thừa bậc 1 của x là 3a;
Hệ số tự do là 4;
Tổng các hệ số của đa thức P(x) là:
1 + 1 + (–2) + 3a + 4 = 3a + 4
Do tổng các hệ số của đa thức P(x) bằng –2 nên ta có:
3a + 4 = –2
Suy ra 3a = –6
Do đó a = –2
Ta chọn phương án C.
Câu 6. Với a ≠ 0; b ≠ 0; m, n ∈ ℕ; kết quả của phép tính axm. bxn bằng:
A. abxm + n;
B. abxm - n;
C. (a – b)xm;
D. (a + b)xm;
Đáp án đúng là: A
Ta có: axm. bxn
= a.b.xm.xn
= abxm + n (a ≠ 0; b ≠ 0; m, n ∈ ℕ)
Vậy ta chọn phương án A.
Câu 7. Tính 2x3. 5x4 ta thu được kết quả là:
A. 10x4;
B. 10x3;
C. 10x7;
D. 10x12.
Đáp án đúng là: C
Ta có: 2x3. 5x4
= 2. 5. x3. x4
= 10x3+4
= 10x7.
Vậy ta chọn phương án C.
Câu 8. Tính –4xm. 3xn + 1 (với m, n ∈ ℕ)ta thu được kết quả là:
A. –12xm + n + 1;
B. 12xm + n + 1;
C. 12xm.(n + 1);
D. –12xm.(n + 1).
Đáp án đúng là: A
Ta có: –4xm. 3xn + 1 (với m, n ∈ ℕ)
= (–4). 3. xm. xn + 1
= –12xm + n + 1.
Vậy ta chọn phương án A.
Câu 9. Tích 2x(x + 1) có kết quả bằng:
A. 2x2 + 2x;
B. 2x2 – 2x;
C. 2x + 2;
D. 2x2 – 2.
Đáp án đúng là: A
Ta có: 2x(x + 1)
= 2x.x + 2x.1
= 2x2 + 2x.
Vậy ta chọn phương án A.
Câu 10. Chọn câu đúng.
A. (x – 1)(x2 + x + 1) = x3 – 1;
B. (x – 1)(x + 1) = 1 – x2;
C. (x + 1)(x – 1) = x2 + 1;
D. (x2 + x + 1)(x – 1) = 1 – x2.
Đáp án đúng là: A
Ta có:
• (x – 1)(x + 1)
= x.x + x – x – 1
= x2 – 1
Do đó phương án B sai, C sai
• (x – 1)(x2 + x + 1)
= x.x2 + x.x + x.1 + (– 1).x2 + (–1). x + (– 1).1
= x3 + x2 + x – x2 – x – 1
= x3 – 1
Do đó phương án A đúng và D sai.
Vậy ta chọn phương án A.
Câu 11. Giả sử 3 kích thước của một hình hộp chữ nhật là x; x + 1; x – 1 (cm) với x > 1. Thể tích hình hộp chữ nhật này là:
A. x3 + x (cm3);
B. x3 – x (cm3);
C. x2 + x (cm3);
D. x2 – x (cm3);
Đáp án đúng là: B
Thể tích hình hộp chữ nhật:
V = x(x + 1)(x – 1)
= (x2 + x)(x – 1)
= x2.x – x2.1 + x.x – x.1
= x3 – x
Vậy thể tích hình hộp chữ nhật là: V = x3 – x (cm3).
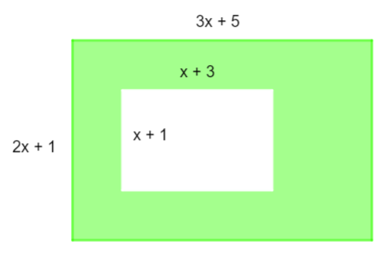
Câu 12. Cho hai hình chữ nhật như hình vẽ.
Đa thức theo biến x biểu thị diện tích của phần được tô màu xanh là:
A. 5x2 + 17x + 8 ;
B. 5x2 + 9x + 2 ;
C. 5x2 + 17x – 2 ;
D. 5x2 – 9x – 2 .
Đáp án đúng là: B
Diện tích hình chữ nhật lớn là:
(3x + 5)(2x + 1)
= 3x.2x + 3x.1 + 5.2x + 5.1
= 6x2 + 3x + 10x + 5
= 6x2 + 13x + 5 (đvdt)
Diện tích hình chữ nhật nhỏ màu trắng bên trong là:
(x + 3)(x + 1)
= x.x + x.1 + 3.x + 3.1
= x2 + x + 3x + 3
= x2 + 4x + 3 (đvdt)
Diện tích phần được tô màu xanh là:
(6x2 + 13x + 5) – (x2 + 4x + 3)
= 6x2 + 13x + 5 – x2 – 4x – 3
= (6x2 – x2) + (13x – 4x) + (5 – 3)
= 5x2 + 9x + 2 (đvdt)
Vậy ta chọn phương án B.
Câu 13. Cho B = (m – 1)(m + 6) – (m + 1)(m – 6). Chọn kết luận đúng.
A. B ⁝ 10 với mọi m ∈ ℤ;
B. B ⁝ 15 với mọi m ∈ ℤ;
C. B ⁝ 9 với mọi m ∈ℤ;
D. B ⁝ 20 với mọi m ∈ ℤ.
Đáp án đúng là: A
Ta có B = (m – 1)(m + 6) – (m + 1)(m – 6)
= m.m + m.6 – (1.m + 1.6) – (m.m – m.6 + 1.m – 1.6)
= m2 + 6m – m – 6 – (m2 – 6m + m – 6)
= m2 + 5m – 6 – m2 + 6m – m + 6
= (m2 – m2) + (5m + 6m – m) + (–6 + 6)
= 10m
Nhận thấy 10 ⁝ 10
Do đó 10.m ⁝ 10
Nên B ⁝ 10 với mọi giá trị nguyên của m.
Ta chọn phương án A.
Câu 14. Cho A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11)
Và B = x(2x + 1) – x2(x + 2) + x3 – x + 3.
Chọn khẳng định đúng trong các khẳng định sau:
A. A = B;
B. A = 25B;
C. A = 25B + 1;
D. A = 2B.
Đáp án đúng là: C
A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11)
= 3x.2x + 3x.3 + 7.2x + 7.3 – (3x.2x + 3x.11 – 5.2x – 5.11)
= 6x2 + 9x + 14x + 21 – (6x2 + 33x – 10x – 55)
= 6x2 + 23x + 21 – 6x2 – 33x + 10x + 55
= (6x2 – 6x2) + (23x – 33x + 10x) + (21 + 55)
= 76
B = x(2x + 1) – x2(x + 2) + x3 – x + 3
= x.2x + x – (x2.x + 2x2) + x3 – x + 3
= 2x2 + x – x3 – 2x2 + x3 – x + 3
= (–x3 + x3) + (2x2 – 2x2) + (x – x) + 3
= 3
Từ đó ta có A = 76; B = 3
Mà 76 = 25.3 + 1 nên A = 25B + 1.
Ta chọn phương án C.
Câu 15. Tính tổng các hệ số của lũy thừa bậc ba, lũy thừa bậc hai và lũy thừa bậc nhất trong kết quả của phép nhân (x2 + x + 1)(x3 – 2x + 1) ta được kết quả:
A. 1;
B. –2;
C. –3;
D. 3.
Đáp án đúng là: C
Ta có (x2 + x + 1)(x3 – 2x + 1)
= x2.x3 + x2.(–2x) + x2.1 + x.x3 + x.(–2x) + x.1 + 1.x3 + 1.(–2x) + 1.1
= x5 – 2x3 + x2 + x4 – 2x2 + x + x3 – 2x + 1
= x5 + x4 + (–2x3 + x3) + (x2 – 2x2) + (x – 2x) + 1
= x5 + x4 – x3 – x2 – x + 1
Hệ số của lũy thừa bậc ba là – 1
Hệ số của lũy thừa bậc hai là – 1
Hệ số của lũy thừa bậc nhất là – 1
Tổng các hệ số này là –1 +(–1) + (–1) = –3.
Vậy ta chọn phương án C.