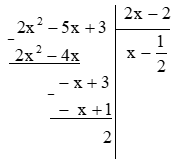Lý thuyết Biểu thức đại số (Chân trời sáng tạo 2024) Toán 7

Lý thuyết Toán lớp 7 Chương 7

Tổng hợp lý thuyết Toán 7 Chương 7

1. Biểu thức số

- Các số được nối với nhau bởi dấu các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa tạo thành một biểu thức.

Chẳng hạn: 3 + 7 – 2; 4. 5: 2; 2. (5 + 8) là những biểu thức.

Những biểu thức như trên còn được gọi là biểu thức số.

2. Biểu thức đại số

Biểu thức bao gồm các số và các chữ (đại diện cho số) được nối với nhau bởi các kí hiệu phép toán cộng, trừ, nhân, chia, nâng lên lũy thừa được gọi là biểu thức đại số.

Trong biểu thức đại số:

- Những chữ đại diện cho một số tùy ý gọi là biến số;

- Những chữ đại diện cho một số xác định gọi là hằng số;

Chú ý:

- Trong biểu thức đại số, vì biến đại diện cho số nên khi thực hiện các phép tính trên các biến, ta có thể áp dụng những tính chất, quy tắc phép toán như trên các số. Chẳng hạn:

x + y = y + z;

(x + y) + z = x + (y + z);

(xy)z = x(yz);

xy = yx;

xxx = x3;

x(y + z) = xy + xz

3. Giá trị của biểu thức đại số

Để tính giá trị của một biểu thức đại số ta thực hiện các bước sau:

- Bước 1: Thay chữ bởi giá trị số đã cho (chú ý các trường hợp phải đặt số trong dấu ngoặc);

- Bước 2: Thực hiện các phép tính (chú ý đến thứ tự thực hiện các phép tính: thực hiện phép lũy thừa, rồi đến phép nhân chia, sau đó là phép cộng trừ).

4. Đa thức một biến

Đơn thức một biến là biểu thức đại số chỉ gồm một số hoặc một biến, hoặc một tích giữa các số và biến đó.

Ta có thể thực hiện các phép tính cộng, trừ, nhân, chia đơn thức cùng một biến.

- Đa thức một biến là tổng của những đơn thức cùng một biến. Đơn thức một biến cũng là đa thức một biến.

Quy ước: P = 0 được gọi là đa thức không.

5. Cách biểu diễn đa thức một biến

- Để thuận tiện cho việc tính toán đối với các đa thức một biến, ta thường viết đa thức đó thành đa thức thu gọn và sắp xếp các đơn thức của chúng theo lũy thừa tăng hoặc giảm của biến.

- Bậc của đa thức một biến (khác đa thức không, đã thu gọn) là số mũ lớn nhất của biến trong đa thức đó.

Chú ý:

- Số thực khác 0 được gọi là đa thức bậc 0.

- Số 0 được gọi là đa thức không có bậc.

6. Giá trị của đa thức một biến

Để tính giá trị của đa thức một biến ta thực hiện các bước sau:

- Bước 1: Thay chữ bởi giá trị số đã cho (chú ý các trường hợp phải đặt số trong dấu ngoặc);

- Bước 2: Thực hiện các phép tính (chú ý đến thứ tự thực hiện các phép tính: thực hiện phép lũy thừa, rồi đến phép nhân chia, sau đó là phép cộng trừ).

7. Nghiệm của đa thức một biến

Nếu đa thức P(x) có giá trị bằng 0 tại x = a thì ta nói a hoặc x = a là một nghiệm của đa thức đó.

Chú ý:

- Một đa thức (khác đa thức không) có thể có 1; 2; 3; ...; n nghiệm hoặc không có nghiệm nào.

- Số nghiệm của một đa thức (khác đa thức 0) không vượt qua bậc của nó.

8. Phép cộng hai đa thức một biến

Để cộng hai đa thức một biến, ta làm một trong hai cách sau:

- Cách 1: Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép cộng.

- Cách 2: Sắp xếp các đơn thức của hai đa thức cùng theo lũy thừa giảm dần (hoặc tăng dần) của biến rồi đặt phép tính theo cột dọc tương ứng sao cho lũy thừa giống nhau ở hai đa thức thẳng cột với nhau rồi thực hiện cộng theo cột.

9. Phép trừ hai đa thức một biến

Để trừ hai đa thức một biến, ta làm một trong hai cách sau:

- Cách 1:Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép trừ.

- Cách 2: Sắp xếp các đơn thức của hai đa thức cùng theo lũy thừa giảm dần (hoặc tăng dần) của biến rồi đặt phép tính theo cột dọc tương ứng sao cho lũy thừa giống nhau ở hai đa thức thẳng cột với nhau rồi thực hiện trừ theo cột.

10. Tính chất của phép cộng đa thức một biến

Tính chất: Cho A, B, C là các đa thức một biến với cùng một biến số.

-Tính chất giao hoán: A + B = B + A;

-Tính chất kết hợp: A + (B + C) = (A + B) + C.

11. Phép nhân đa thức một biến

Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.

12. Phép chia đa thức một biến

Trường hợp 1: Chia đa thức cho đa thức (chia hết)

Cho hai đa thức P và Q (với Q ≠ 0). Ta nói đa thức P chia hết cho đa thức Q nếu có đa thức M sao cho P = Q. M.

Ta gọi P là đa thức bị chia, Q là đa thức chia và M là đa thức thương (gọi tắt là thương).

Kí hiệu M = P : Q hoặc M = $\frac{P}{Q}$.

Chú ý: Để thực hiện phép chia đa thức, người ta thường viết các đa thức đó thành đa thức thu gọn và sắp xếp các đơn thức theo lũy thừa giảm dần rồi thực hiện phép chia.

Trường hợp 2: Chia đa thức cho đa thức (phép chia có dư)

Khi chia đa thức A cho đa thức B với thương là Q, dư là R thì A = B. Q + R, trong đó bậc của R nhỏ hơn bậc của B.

13. Tính chất của phép nhân đa thức một biến

Tính chất: Cho A, B, C là các đa thức một biến với cùng một biến số.

-Tính chất giao hoán: A. B = B. A;

-Tính chất kết hợp: A. (B. C) = (A. B). C.

Bài tập Tổng hợp Toán 7 Chương 7

Bài 1: Thực hiện phép chia:

a) (8x6 − 4x5 + 12x4 – 20x3): 4x3;

b) (2x2 − 5x + 3): (2x – 3).

Hướng dẫn giải:

a) (8x6 − 4x5 + 12x4 – 20x3) : 4x3

= (8x6 : 4x3) – (4x5 : 2x3) + (12x4 : 4x3) – (20x3 : 4x3)

= 2x3 − 2x2 + 3x – 5;

b) Ta có:

Vậy (2x2− 5x + 3) = (2x – 3)$\left(x-\frac{1}{2}\right)$ + 2.

Bài 2: Rút gọn biểu thức bằng cách nhanh nhất:

a) 5. (x2 + 3).$\frac{2}{5}$;

b) (x – 2).(2x3 – x2 + 1) + (x – 2)x2(1 – 2x).

Hướng dẫn giải:

a) 5. (x2+ 3). $\frac{2}{5}$= $\left(5.\frac{2}{5}\right)$. (x2+ 3)

=2. (x2+ 3) = 2x2 + 6

b) (x – 2)(2x3 – x2 + 1) + (x – 2)x2(1 – 2x)

= (x – 2)(2x3 – x2 + 1) + (x – 2)(x2.1 – x2.2x)

= (x – 2)(2x3 – x2 + 1) + (x – 2)(x2 – 2x3)

= (x – 2)(2x3 – x2 + 1 + x2 – 2x3)

= (x – 2).1

= (x – 2).

Bài 3:Không thực hiện phép chia, hãy xét xem đa thức A có chia hết cho đa thức B hay không?

a) A = 15x4 – 8x3 + x2; B = $\frac{1}{2}$x2;

b) A = x2 – 2x + 1; B = x + 1.

Hướng dẫn giải:

a)Ta có: Vì 15x4; 8x3; x2 đều chứa phần từ x2 nên đều chia hết cho $\frac{1}{2}$x2

Do đó đa thức A chia hết cho B.

b) Ta có:

A = x2 + 2x + 1

= x(x + 1) + (x + 1)

= (x + 1)(x + 1)

= (x + 1)2

Vì (x + 1)2 chứa phần tử (x + 1) nên chia hết cho (x + 1)

Do đó đa thức A chia hết cho B.

Bài 4: Hãy viết biểu thức đại số biểu thị

a)Tổng của hai lần x và ba lần y;

b)Hiệu của x và y;

c)Tích của tổng x và y với hiệu x và y.

Hướng dẫn giải:

a)Hai lần x là: 2x;

Ba lần y là: 3y;

Biểu thức đại số biểu thị tổng của hai lần x và ba lần y là: 2x + 3y.

b)Biểu thức đại số biểu thị hiệu của x và y là: x – y.

c)Tổng x và y là: x + y;

Hiệu x và y là: x – y;

Biểu thức đại số biểu thị tích của tổng x và y với hiệu x và y là: (x + y).(x – y).

Bài 5: Cho A = 4x2y – 5 và B = 3x2y + 6 x2y2 + 3xy2. So sánh A và B khi x = –1, y = 3.

Hướng dẫn giải:

+ Thay x = –1, y = 3 vào biểu thức A ta được:

A = 4x2y – 5 = 4.(–1)2.3 – 5

= 4. 1. 3 – 5 = 12 – 5 = 7.

+ Thay x = –1, y = 3 vào biểu thức B ta được:

B = 3x2y + 6x2y2 + 3xy2

= 3.(–1)2.3 + 6.(–1)2.32 + 3.(–1).32

= 3.1.3 + 6.1.9 – 3. 9 = 9 + 54 – 27 = 36.

Vì 7 < 36 nên A < B.

Vậy A < B khi x = –1, y = 3.

Bài 6: Một mảnh vườn hình chữ nhật có chiều dài là x và diện tích là 84 cm2. Tính chiều rộng của mảnh vườn theo x và tại x = 12 cm.

Hướng dẫn giải:

Chiều rộng mảnh vườn theo x là: $\frac{84}{x}$(cm)

Tại x = 12, chiều rộng của mảnh vườn là: $\frac{84}{12}=7$(cm)

Vậy chiều rộng mảnh vườn theo x là: $\frac{84}{x}$(cm)

Chiều rộng của mảnh vườn tại x = 12 cm là 7 cm.

Bài 7: Giá trị của biểu thức N = 5x2 + 10x – 20 tại |x – 1| = 1

Hướng dẫn giải:

Ta có: |x – 1| = 1

x – 1 = 1 hoặc x – 1 = – 1

x = 2 hoặc x = 0

Trường hợp 1: x =2, thay vào biểu thức N ta được:

N = 5x2 + 10x – 20 = 5.22 + 10.2 – 20

= 5.4 + 20 – 20 = 20;

Trường hợp 2: x = 0, thay vào biểu thức N ta được:

N = 5x2 + 10x – 20 = 5.02 + 10.0 – 20

= 0 – 0 – 20 = – 20.

Vậy tại |x – 1| = 1 thì N = 20 hoặc N = – 20.

Bài 8: Hãy cho biết biểu thức nào sau đây là đa thức một biến:

3xy2 + xy; $\frac{1}{2}x+4$; x3 + 3z; x4 – 6x + 7; 1 + 4.23.

Hướng dẫn giải:

Ta xét các đa thức sau:

3xy2 + xy là đa thức hai biến x và y;

$\frac{1}{2}x+4$ là đa thức biến x;

x3 + 3z là đa thức hai biến x và z;

x4 – 6x + 7 là đa thức biến x;

1 + 4.23 là đa thức không chứa biến.

Vậy các đa thức một biến là: $\frac{1}{2}x+4$; x4 – 6x + 7.

Bài 9: Cho đa thức P(x) = 7 + 4x2 + 3x3 – 6x + 4x3 – 5x2.

a) Hãy viết đa thức thu gọn của đa thức P và sắp xếp các đơn thức theo lũy thừa giảm dần của biến;

b) Xác định bậc của P(x) và tìm các hệ số.

Hướng dẫn giải:

a) Ta có: P = 7 + 4x2 + 3x3 – 6x + 4x3 – 5x2

= (3x3 + 4x3) + (4x2 – 5x2) – 6x + 7

= 7x3 – x2 – 6x + 7.

b) Trong đa thức trên, số mũ cao nhất của x là 3 nên đa thức P(x) có bậc là 3.

Hệ số của x3 là 7, gọi là hệ số cao nhất. Hệ số của x2 là – 1; hệ số của x là – 6 và 7 là hệ số tự do.

Bài 10. Tính giá trị của đa thức Q(y) = 3y4 + 4y2 – 5 khi y = $\frac{1}{2}$.

Hướng dẫn giải:

Ta có: $Q\left(\frac{1}{2}\right)$ = $3.{\left(\frac{1}{2}\right)}^4+4.{\left(\frac{1}{2}\right)}^2-5$

$=3.\frac{1}{16}+4.\frac{1}{4}-5=\frac{3}{16}+1-5$

$=\frac{3}{16}-4=\frac{-61}{16}$.

Vậy giá trị của Q(y) khi y =$\frac{1}{2}$ là $\frac{-61}{16}$.

Bài 11: Cho hai đa thức f(x) = 4x4 – 2ax2 + (a + 1).x + 2 và g(x) = 2ax + 5.

Tìm a để f(1) = g(2).

Hướng dẫn giải:

Ta có: f(1) = 4.14 – 2a.12 + (a + 1). 1 + 2

= 4 – 2a + a + 1 + 2

= 7 – a.

g(2) = 2a.2 + 5 = 4a + 5.

Để f(1) = g(2) thì:

7 – a = 4a + 5

5a = 2

a = $\frac{2}{5}$

Vậy a = $\frac{2}{5}$.

Bài 12: Cho hai đa thức f(x) = 3x2 + 2x − 5 và g(x) = −3x2 − 2x + 2. Tính h(x) = f(x) + g(x) và tìm bậc của h(x).

Hướng dẫn giải:

Ta có: h(x) = f (x) + g (x)

= (3x2 + 2x− 5) + (−3x2 − 2x + 2)

= 3x2 + 2x − 5 − 3x2 − 2x + 2

= (3x2 − 3x2) + (2x − 2x) + (−5 + 2) = −3.

Vậy h(x) = −3 và bậc của h(x) là 0.

Bài 13:Cho hai đa thức f(x) = 5x4 + x3 − x2 + 1 và g(x) = −5x4 − x2 + 2.

Tính k(x) = f(x) − g(x) và tìm bậc của k(x).

Hướng dẫn giải:

Ta có: k(x) = f(x) − g(x)

= (5x4 + x3 − x2 + 1) −(−5x4 − x2 + 2)

= 5x4 + x3 − x2 + 1 + 5x4 + x2 − 2

= (5x4 + 5x4) + x3 + (−x2 +x2) + (1 − 2)

= 10x4 + x3 – 1.

Vậy k(x) =10x4 + x3 − 1và bậc của k(x) là 4.

Bài 14. Cho f (x) = x5 − 3x4 + x2 − 5 và g (x) = 2x4 +7x3 − x2 + 6. Tính hiệu f(x) − g(x) rồi sắp xếp kết quả theo lũy thừa tăng dần của biến.

Hướng dẫn giải:

Ta có: f(x) − g(x) = (x5 − 3x4 + x2 −5) – (2x4 + 7x3 − x2 + 6)

= x5 − 3x4 + x2 − 5 – 2x4 – 7x3 + x2 – 6

= x5 + (−3x4 − 2x4) – 7x3 + (x2 + x2) + (− 5− 6)

= x5 − 5x4 − 7x3 + 2x2 −11.

Vậy hiệu f(x) − g(x) và sắp xếp kết quả theo lũy thừa tăng dần của biến ta được:

11 + 2x2 −7x3 − 5x4 + x5.

Bài 15: Tìm đa thức h(x) biết f(x) − h(x) = g(x).

Trong đó: f(x) = x2 + x + 1; g(x) = 4 − 2x3 + x4 + 7x5.

Hướng dẫn giải:

Ta có: f(x) − h(x) = g(x).

Suy ra: h(x) = f(x)− g(x).

= (x2 + x + 1) – (4 − 2x3 + x4 + 7x5)

= x2 + x + 1 – 4 + 2x3 – x4 – 7x5

= −7x5− x4 + 2x3 + x2 + x – 3.

Vậy h(x) = −7x5− x4+ 2x3 + x2 + x – 3.

Bài 16: Thực hiện phép nhân

a) (4x – 3)(x + 2);

b) (5x + 2)(–x2 + 3x +1);

c) (2x2 – 7x + 4)(–3x2 + 6x + 5).

Hướng dẫn giải:

a) (4x – 3)(x + 2) = 4x(x + 2) – 3(x + 2)

= 4x2 + 8x – 3x – 6 = 4x2 + 5x – 6;

b) (5x + 2)(–x2 + 3x +1)

= 5x(–x2 + 3x +1) + 2(–x2 + 3x +1)

= –5x3 + 15x2 + 5x – 2x2 + 6x + 2

= –5x3 + (15x2– 2x2) + (5x + 6x) + 2

= –5x3 + 13x2 + 11x + 2.

c) (2x2 – 7x + 4)(–3x2 + 6x + 5)

= 2x2(–3x2 + 6x + 5) – 7x(–3x2 + 6x + 5) + 4(–3x2 + 6x + 5)

= –6x4 + 12x3 + 10x2 + 21x3 – 42x2 – 35x – 12x2 + 24x + 20

= –6x4 + (12x3 + 21x3) + (10x2 – 42x2 – 12x2) + (– 35x + 24x) + 20

= –6x4 + 33x3 – 44x2 – 11x + 20.