Lý thuyết Số thực. Giá trị tuyệt đối của một số thực (Chân trời sáng tạo 2024) Toán 7

Lý thuyết Toán lớp 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực

Video giải Toán 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực - Chân trời sáng tạo

A. Lý thuyết Số thực. Giá trị tuyệt đối của một số thực

1. Số thực và tập hợp các số thực

– Ta gọi chung số hữu tỉ và số vô tỉ là số thực.

– Tập hợp số thực được kí hiệu ℝ.

Cách viết x ∈ ℝ cho ta biết x là một số thực.

– Mỗi số thực chỉ có một trong hai dạng biểu diễn thập phân sau:

+ Dạng thập phân hữu hạn hay vô hạn tuần hoàn nếu số đó là số hữu tỉ.

+ Dạng thập phân vô hạn không tuần hoàn nếu số đó là số vô tỉ.

Ví dụ: Ta có các số 5; –3 ; 0,14 ; $-\frac{8}{7}$ ; $3\frac{1}{8}$ ; $\sqrt{11}$ ; π ; ….là các số thực.

Ta viết 5 ∈ ℝ ; –3 ∈ ℝ ; 0,14 ∈ ℝ ; $-\frac{8}{7}$ ∈ ℝ ; $3\frac{1}{8}$ ∈ ℝ; $\sqrt{11}$ ∈ ℝ ; π ∈ ℝ ; …

Chú ý: Trong các tập hợp đã học, tập hợp số thực là “rộng lớn” nhất bao gồm tất cả các số tự nhiên, số nguyên, số hữu tỉ và cả số vô tỉ.

– Trong tập hợp các số thực, ta cũng có các phép tính với các tính chất tương tự như các phép tính trong tập hợp các số hữu tỉ mà ta đã biết.

2. Thứ tự trong tập hợp các số thực

– Các số thập phân hữu hạn hoặc vô hạn đều có thể so sánh tương tự như so sánh hai số thập phân hữu hạn, đó là so sánh phần số nguyên, rồi đến phần thập phân thứ nhất, phần thập phân thứ hai, …

– Ta có thể so sánh hai số thực bằng cách so sánh hai số thập phân (hữu hạn hoặc vô hạn) biểu diễn chúng.

Do vậy: Với hai số thực x, y bất kì, ta luôn có hoặc x < y hoặc x > y hoặc x = y.

Chú ý: Với hai số thực dương a và b, ta có:

Nếu a > b thì $\sqrt{a}>\sqrt{b}$.

Ví dụ: So sánh hai số thực:

a) 5,(56) và 5,566;

b) $\sqrt{3}$ và 1,733;

c) –1,024 và –1,025;

d) $\sqrt{8}$ và 3.

Hướng dẫn giải

a) Số 5,(56) = 5,565656… < 5,566 (do phần thập phân thứ ba của hai số ta thấy 5 < 6).

Vậy 5,(56) < 5,566.

b) Ta có: $\sqrt{3}$ = 1,73205… < 1,733 (do phần thập phân thứ ba của hai số ta thấy 2 < 3).

Vậy $\sqrt{3}$ < 1,733.

c) Ta có: 1,024 < 1,025 (do phần thập phân thứ ba của hai số ta thấy 4 < 5)

Suy ra: –1,024 > –1,025.

Vậy –1,024 > –1,025.

d) Do 8 < 9 nên ta có $\sqrt{8}<\sqrt{9}$, tức là $\sqrt{8}$ < 3 (vì $\sqrt{9}$ = 3).

Vậy $\sqrt{8}$ < 3.

3. Trục số thực

Ta đã biết một hình vuông có cạnh bằng 1 có độ dài đường chéo là $\sqrt{2}.$

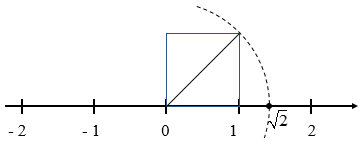
– Trên trục số ta biểu diễn được số vô tỉ $\sqrt{2}.$. Vì vậy, không phải mỗi điểm trên trục số đều biểu diễn một số hữu tỉ, nghĩa là các điểm biểu diễn số hữu tỉ không lấp đầy trục số.

Người ta chứng minh được rằng:

+  Mỗi số thực được biểu diễn bởi một điểm trên trục số

+ Ngược lại, mỗi điểm trên trục số biểu diễn một số thực.

Vì vậy, ta gọi trục số là trục số thực.

Chú ý:

– Điểm biểu diễn số thực x trên trục số được gọi là điểm x. 

– Nếu x < y thì trên trục số nằm ngang, điểm x ở bên trái điểm y.

Ví dụ: Ta có: $\sqrt{2}.$ = 1,414213562… < 1,5.

Vậy điểm $\sqrt{2}.$ nằm bên trái điểm 1,5 trên trục số nằm ngang.

4. Số đối của một số thực

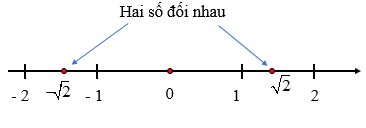
– Hai số thực có điểm biểu diễn trên trục số cách đều điểm gốc O và nằm về hai phía ngược nhau là hai số đối nhau, số này gọi là số đối của số kia.

– Số đối của số thực x kí hiệu là –x.

– Ta có x + (– x) = 0.

Ví dụ:  Số đối của số $\sqrt{2}$ là $-\sqrt{2}$, số đối của $-\sqrt{2}$ là $\sqrt{2}$.

5. Giá trị tuyệt đối của một số thực

Giá trị tuyệt đối của một số thực x là khoảng cách từ điểm x đến điểm 0 trên trục số.

Giá trị tuyệt đối của một số thực x được kí hiệu là |x|.

Nhận xét: Ta có$\left|x\right|\text{ = }\left\{\begin{array}{c}x\text{ khi x > 0}\\ -x\text{ \hspace{0.17em}khi x < 0}\\ 0\text{ \hspace{0.17em}khi x =\hspace{0.17em} 0}\end{array}\right.$

Vậy giá trị tuyệt đối của một số thực x luôn là số không âm:

|x| ≥ 0 với mọi số thực x.

Ví dụ:

a)

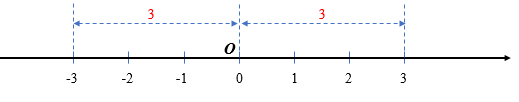
– Khoảng cách từ điểm –3 đến điểm 0 là 3 nên |–3| = 3.

– Khoảng cách từ điểm 3 đến gốc 0 là 3 nên |3| = 3.

b) Vì –2 < 0 nên |–2| = –(–2) = 2.

B. Bài tập tự luyện

1. Bài tập trắc nghiệm

Câu 1. Sắp xếp các số thực $-\frac{2}{3};\sqrt{2};0,2\left(14\right);\frac{4}{7};0,123$ theo thứ tự từ giảm dần ta được:

A. $-\frac{2}{3}$;0,123; 0,2(14); $\frac{4}{7}$; $\sqrt{2}$;

B. $-\frac{2}{3}$;$\frac{4}{7}$; 0,123; 0,2(14); $\sqrt{2}$;

C. $\sqrt{2}$; $\frac{4}{7}$; 0,123; 0,2(14); $-\frac{2}{3}$;

D. $\sqrt{2}$; $\frac{4}{7}$; 0,2(14); 0,123; $-\frac{2}{3}$.

Hướng dẫn giải

Đáp án đúng là: D

Ta chia dãy số trên thành 2 nhóm:

– Nhóm 1: $-\frac{2}{3}$

– Nhóm 2: $\sqrt{2};0,2\left(14\right);\frac{4}{7};0,123$

Xét nhóm 2 ta có:

$\sqrt{2}=1,\mathrm{414...}$; 0,2(14) = 0,214… và $\frac{4}{7}=0,\mathrm{571...}$

Mà 1,414…> 0,571…> 0,214…> 0,123

Nên $\sqrt{2}$> $\frac{4}{7}$> 0,2(14) > 0,123.

Vì 0,123 là số dương, $-\frac{2}{3}$ là số âm mà số dương luôn lớn hơn số âm nên 0,123 >$\sqrt{2}$.

Suy ra, $\sqrt{2}$> $\frac{4}{7}$ > 0,2(14) > 0,123 > $-\frac{2}{3}$.

Vậy sắp xếp các số đã cho theo thứ tự giảm dần ta có:

$\sqrt{2}$; $\frac{4}{7}$; 0,2(14); 0,123; $-\frac{2}{3}$.

Ta chọn phương án D.

Câu 2. Khẳng định nào sau đây sai?

A. $\sqrt{4}$ ∉ ?;

B. $\sqrt{3}\in \mathbb{Q};$

C. $\frac{2}{3}\in ℝ;$

D. $-9\in \mathbb{Z}.$

Hướng dẫn giải

Đáp án đúng là: B

Ta có:

• $\sqrt{4}=2$.

Vì 2 là số tự nhiên nên không phải là số vô tỉ.

Do đó $\sqrt{4}$ ∉ ? là khẳng định đúng. Nên phương án A đúng.

• $\sqrt{3}=1,\mathrm{732...}$ .

Vì 1,732… là số thập phân vô hạn không tuần hoàn nên $\sqrt{3}$là số vô tỉ.

Suy ra $\sqrt{3}$ ∈ ?. Do đó, phương án B sai.

• $\frac{2}{3}=0,\mathrm{66...}=0,\left(6\right).$

Vì 0,(6) là số thập phân vô hạn tuần hoàn nên $\frac{2}{3}$ là số hữu tỉ.

Mà số vô tỉ là số thực. Suy ra, $\frac{2}{3}\in \mathrm{\mathbb{Z}}$. Do đó, phương án C đúng.

• Số −9 là số nguyên âm nên $-9\in \mathrm{\mathbb{Z}}$. Do đó, phương án D đúng.

Vậy chọn phương án B.

Câu 3. Chữ số thích hợp điền cho $\boxed{?}$ trong phép so sánh $-95,\left(112\right)<-95,\boxed{?}12112$ là:

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án đúng là: A.

Do $-95,\left(112\right)<-95,\boxed{?}12112$ nên $95,\left(112\right)>95,\boxed{?}12112.$

Ta có 95,(112) = 95,112112…

Xét hai số 95,112112… và $95,\boxed{?}12112$ ta thấy hai số này có phần nguyên giống nhau nên ta xét đến phần thập phân của chúng.

Ở hàng phần trăm ta thấy cả hai số đều là 1 nên để $95,112112\dots >95,\boxed{?}12112$ thì hàng phần mười của số 95,112112… phải lớn hơn hàng phần mười của số $95,\boxed{?}12112$.

Tức là $1>\boxed{?}$  do đó $\boxed{?}=0$ 

Vậy số điền vào $\boxed{?}$ là số 0.

Ta chọn phương án A.

2. Bài tập tự luận

Bài 1. Tìm số đối của các số sau: $-\sqrt{6}$; 3,(2); 5,13 ; – π; |–12,21|.

Hướng dẫn giải

Số đối của $-\sqrt{6}$ là $-(-\sqrt{6})=\sqrt{6};$

Số đối của 3,(2) là –3,(2);

Số đối của 5,13 là –5,13;

Số đối của –π là –(–π) = π.

Số đối của số |–12,21| = 12,21 là số –12,21.

Bài 2. Tính:

a) |–0,6|;

b) $\left|1\frac{3}{4}\right|;$

c) –|–3,6| : 1,2;

d) |−$\sqrt{16}$| + $\sqrt{\left|-25\right|}.$

Hướng dẫn giải

a) |–0,6| = 0,6;

b) $\left|1\frac{3}{4}\right|=1\frac{3}{4}=\frac{7}{4}.$

c) –|–3,6| : 1,2

= –[–(–3,6)] : 1,2

= –[3,6] : 1,2

= –3.

d) |−$\sqrt{16}$| + $\sqrt{\left|-25\right|}.$

= $\sqrt{16}+\sqrt{25}$

= 4 + 5

= 9.

Bài 3. Tìm x, y biết :

a) |x| = 1;

b) | x – 1| = –5;

c) | y + 0,5| = 4.

Hướng dẫn giải

a) |x| = 1 nên x = 1 hoặc x = –1.

b) | x – 1| ≥ 0 với mọi số thực x.

Mà –5 < 0.

Vậy không có số thực x nào thỏa mãn | x – 1| = –5

c) | y + 0,5| = 4 nên y + 0,5 = 4 hoặc y + 0,5 = –4

• Với y + 0,5 = 4 thì y = 4 – 0,5 = 3,5

• Với y + 0,5 = – 4 thì y = –4 – 0,5 = –5,5.

Vậy y = 3,5; y = –5,5 thỏa mãn | y + 0,5| = 4.