Lý thuyết Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác (Chân trời sáng tạo 2024) Toán 7

Lý thuyết Toán lớp 7 Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

Video giải Toán 7 Bài 3: Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác - Chân trời sáng tạo

A. Lý thuyết Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác

1. Hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác

– Hình có ba mặt bên là hình chữ nhật và hai mặt đáy là hình tam giác được gọi là hình lăng trụ đứng tam giác.

– Hình có bốn mặt bên là hình chữ nhật và hai mặt đáy là hình tứ giác được gọi là hình lăng trụ đứng tứ giác.

Ví dụ:

a) Hình ABC.DEF là hình lăng trụ đứng tam giác.

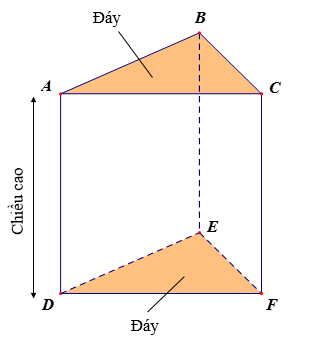
• A, B, C, D, E, F gọi là các đỉnh.

• Ba mặt bên ACFD, BCFE, ABED là các hình chữ nhật.

• Các đoạn thẳng AD, BE, CF bằng nhau và song song với nhau, chúng gọi là các cạnh bên.

• Mặt ABC và mặt DEF song song với nhau và được gọi là hai mặt đáy (gọi tắt là đáy).

• Độ dài cạnh AD được gọi là chiều cao của hình lăng trụ.

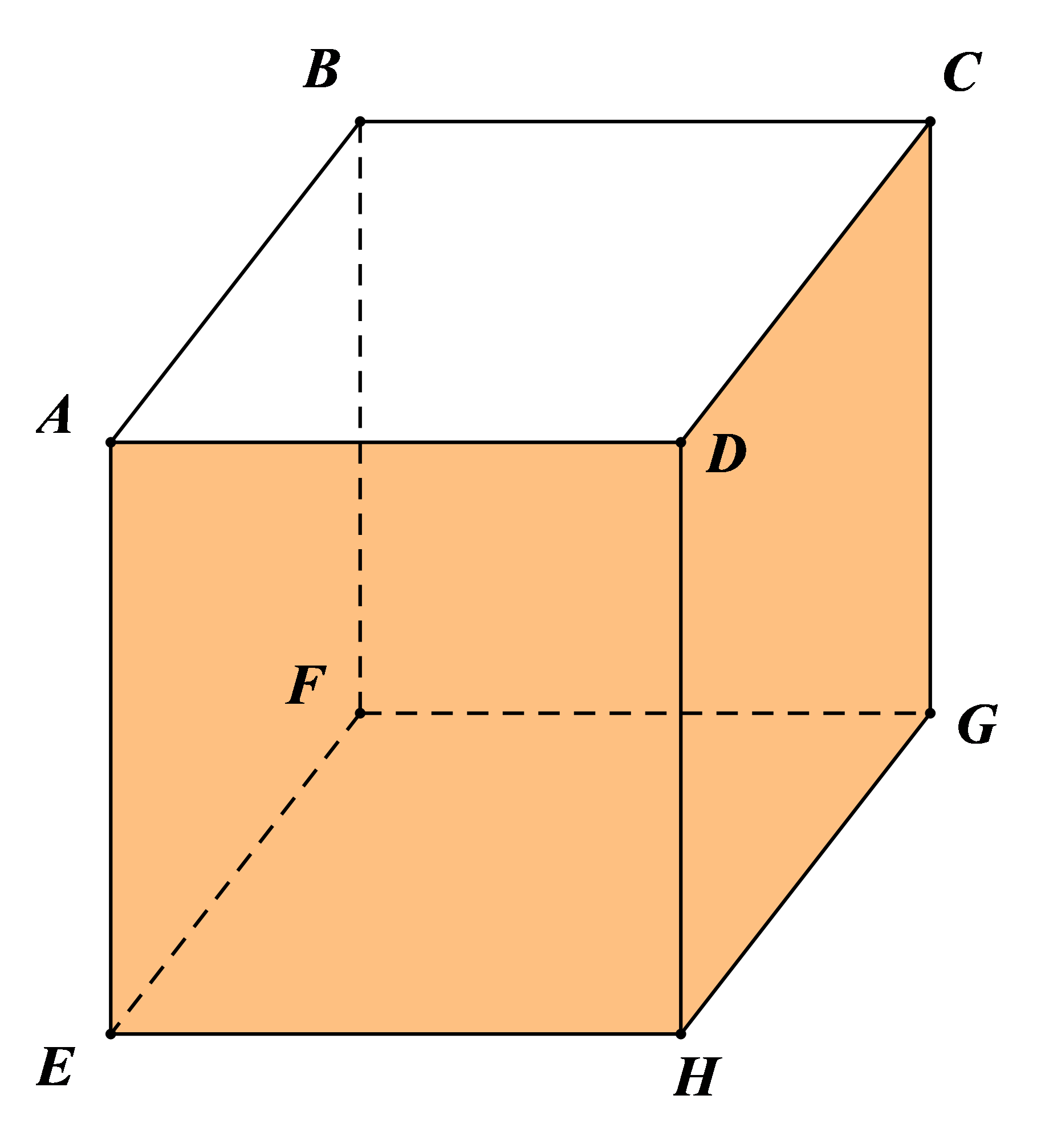
b) Hình ABCD.EFGH là hình lăng trụ đứng tứ giác

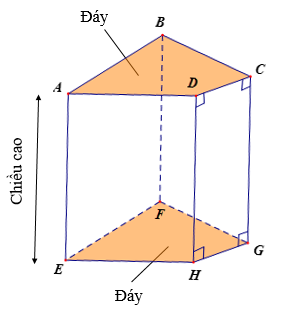
• Hai mặt đáy là tứ giác ABCD và EFGH.

• Các mặt bên ABFE, BCGF, CDHG, ADHE đều là các hình chữ nhật.

Chú ý: Hình hộp chữ nhật, hình lập phương là lăng trụ đứng tứ giác.

2. Tạo lập hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác

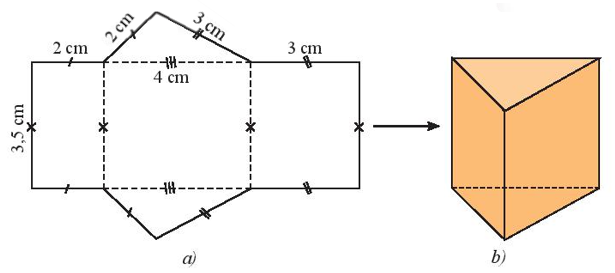
Ví dụ: Tạo lập hình lăng trụ đứng tam giác có kích thước ba cạnh đáy là 2 cm, 3 cm, 4 cm và chiều cao 3,5 cm. 

Hướng dẫn giải

– Trên một tấm bìa vẽ ba hình chữ nhật và hai tam giác với kích thước như hình a.

– Cắt miếng bìa như hình vẽ rồi gấp theo các đường nét đứt, ta được hình lăng trụ đứng tam giác như hình b.

B. Bài tập tự luyện

B.1. Bài tập trắc nghiệm

Câu 1. Cho tấm bìa sau:

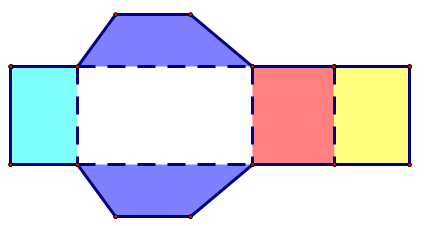
Khi gấp tấm bìa lại theo đường nét đứt, ta được hình lăng trụ đứng nào trong các hình lăng trụ đứng dưới đây:

A.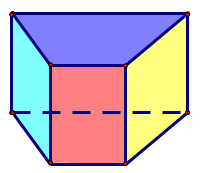 

B.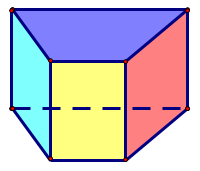 

C.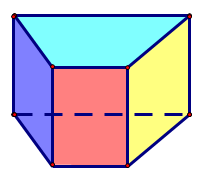 

D.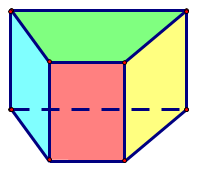 

Hướng dẫn giải:

Đáp án đúng là: B

+ Ta thấy mặt đáy có màu xanh biển và không có tấm bìa nào màu xanh lá cây.

Do đó ta loại phương án C và D.

+ Theo thứ tự từ trái sang phải thì các hình chữ nhật có màu sắc lần lượt là: màu xanh da trời, không màu, màu hồng, màu vàng.

Do đó khi tạo lập lên hình lăng trụ đứng tứ giác thì ta cũng được các mặt bên có thứ tự màu như vậy.

Tức là nếu ta đặt mặt không màu là “mặt sau”, mặt màu xanh da trời là “mặt bên tay trái” thì:

• “Mặt trước” sẽ là mặt màu vàng;

• “Mặt bên tay phải” sẽ là mặt màu hồng.

Vậy ta chọn phương án B.

Câu 2. Cho hình lăng trụ đứng ABC.DEF biết AB = 3 cm; AC = 4 cm; BC = 5 cm. Chu vi tam giác DEF là:

A. 10 cm;

B. 11 cm;

C. 12 cm;

D. 13 cm.

Hướng dẫn giải

Đáp án đúng là: C

Ta có hình lăng trụ đứng tam giác ABC.DEF như hình vẽ dưới đây:

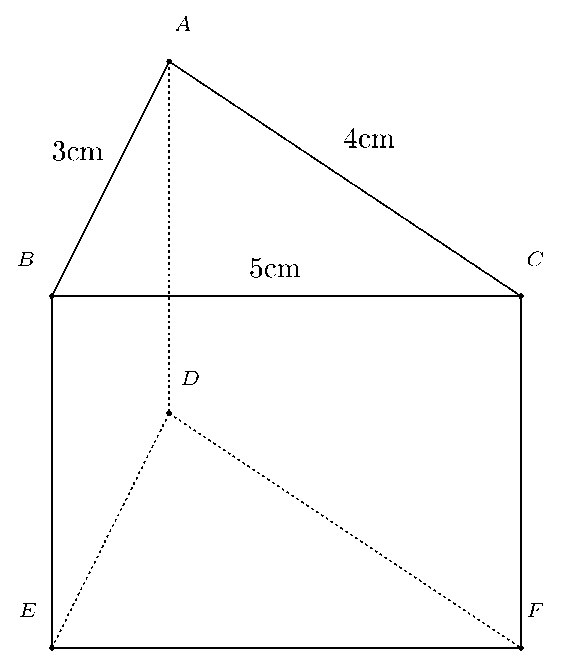
Mặt bên ABED là hình chữ nhật nên AB = DE = 3 cm;

Mặt bên ACFD là hình chữ nhật nên AC = DF = 4 cm;

Mặt bên BCFE là hình chữ nhật nên BC = EF = 5 cm;

Chu vi tam giác DEF là:

DE + DF + EF = 3 + 4 + 5 = 12 (cm).

Vậy ta chọn phương án C.

Câu 3. Cho hình bên.

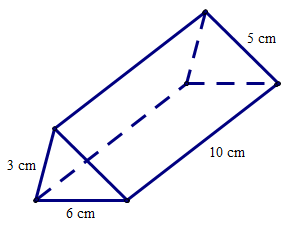
Hình lăng trụ đứng tam giác với kích thước như hình bên được tạo lập từ tấm bìa nào trong các tấm bìa sau đây:

A.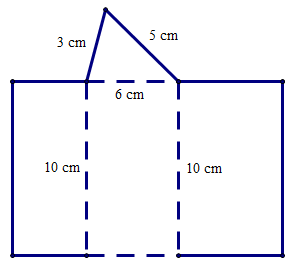 

B.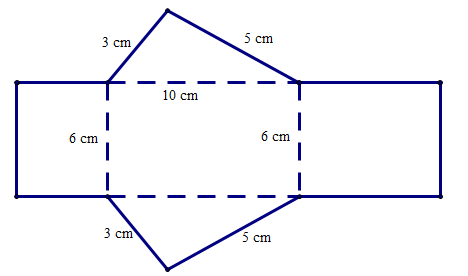 

C.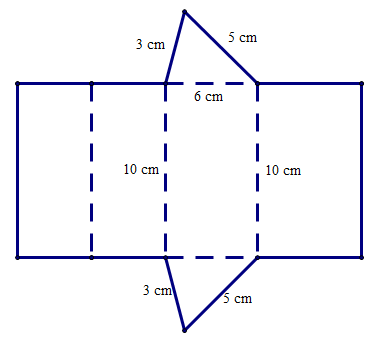 

D.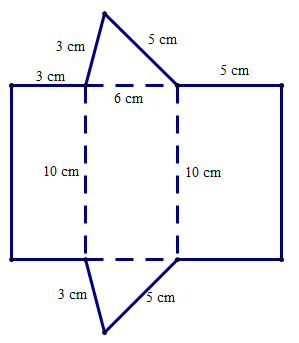 

Hướng dẫn giải:

Đáp án đúng là: D

Ta xét các phương án:

• Xét phương án A: Chỉ có một tam giác để tạo lâp lên mặt đáy là tam giác nên tấm bìa này không tạo lập được hình lăng trụ tam giác.

• Xét phương án B:

Quan sát hình lăng trụ đứng tam giác ta thấy mặt đáy là tam giác có độ dài ba cạnh là 3 cm, 5 cm và 6 cm.

Mà tấm bìa trong phương án B ta thấy tam giác có độ dài ba cạnh là 3 cm, 5 cm và 10 cm.

Do đó tấm bìa này không tạo lập được hình lăng trụ tam giác cần tạo lập.

• Xét phương án C: Có 4 hình chữ nhật nên tạo lập được 4 mặt bên do đó tấm bìa này không tạo lập được hình lăng trụ tam giác.

Vậy ta chọn phương án D.

B.2. Bài tập tự luận

Bài 1. Quan sát hình lăng trụ đứng tam giác sau:

a) Chỉ ra hai mặt đáy và các mặt bên của hình lăng trụ đứng tam giác.

b) Những cạnh nào có độ dài bằng độ dài của cạnh AD?

Hướng dẫn giải

a) Hai mặt đáy là tam giác ABC và tam giác DEF.

Các mặt bên là các hình chữ nhật ABED, BCFE, ACFD.

b) Hình lăng trụ đứng tam giác ABC.DEF có các mặt bên: ABED, ACFD đều là hình chữ nhật.

Suy ra: AD = BE; AD = CF.

Vậy các cạnh có độ dài bằng độ dài cạnh AD là BE và CF .

Bài 2. Tạo lập hình lăng trụ đứng tứ giác có đáy là hình vuông cạnh 3 cm và chiều cao 5 cm.

Hướng dẫn giải

– Vẽ lên tấm bìa bốn hình chữ nhật có chiều dài là 5 cm, chiều rộng là 3 cm và hai hình vuông có cạnh là 3 cm như hình vẽ,

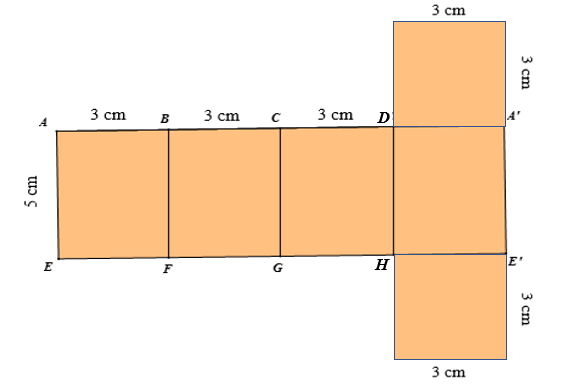
– Cắt tấm bìa và gấp các cạnh BF, CG, DH, DA’, HE’ sao cho AE trùng với A'E' và các cạnh còn lại của hình vuông trên trùng với các cạnh AB, BC, CD; các cạnh còn lại của hình vuông dưới trùng với các cạnh EF, FG, GH.

Khi đó, ta được hình lăng trụ đứng tứ giác ABCD.EFGH có đáy là hình vuông cạnh là 3 cm và chiều cao là 5 cm.