30 câu Trắc nghiệm Hình hộp chữ nhật – Hình lập phương (có đáp án 2024) – Toán 7 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 1: Hình hộp chữ nhật – Hình lập phương Lũy thừa của một số hữu tỉ đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 1.
Trắc nghiệm Toán 7 Bài 1: Hình hộp chữ nhật – Hình lập phương
I. Nhận biết
Câu 1. Hãy chọn khẳng định sai.
Hình hộp chữ nhật ABCD.A'B'C'D' có:
A. 8 đỉnh;
B. 4 mặt bên;
C. 6 cạnh;
D. 6 mặt.
Đáp án: C
Giải thích:
Hình hộp chữ nhật này có 12 cạnh: AB; BC; CD; DA; A'B'; C'D'; B'C'; D'A'; AA'; BB'; CC'; DD'.
Do đó phương án C là khẳng định sai.
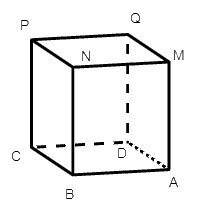
Câu 2. Có bao nhiêu góc vuông ở đỉnh A của hình hộp chữ nhật ABCD. MNPQ?
A. 1;
B. 2;
C. 3;
D. 4.
Câu 3. Trong các hình hộp dưới đây hình nào là hình lập phương?
A. 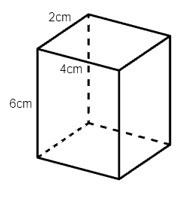
B. 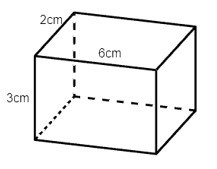
C. 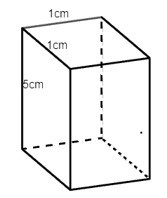
D. 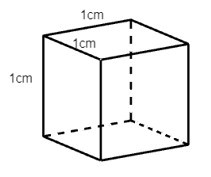
Đáp án: D
Giải thích:
Ta thấy hình D là hình hộp có các cạnh bằng nhau nên hình D là hình lập phương.
Câu 4. Mặt nào sau đây không phải là mặt bên của hình hộp chữ nhật ABCD.EFGH?
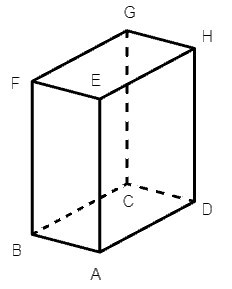
A. ABCD;
B. BFGC;
C. GCDH;
D. BFEA.
Đáp án: A
Giải thích:
Hình hộp chữ nhật ABCD.EFGH có 4 mặt bên là: BFEA; EHDA; GCDH; BFGC.
Mặt ABCD là mặt đáy.
Do đó mặt không phải mặt bên của hình chữ nhật là ABCD.
Câu 5. Số đường chéo của hình hộp chữ nhật ABCD. EFGH:
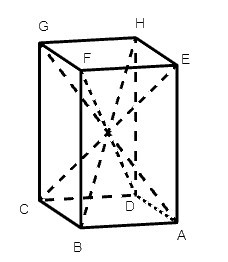
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: D
Giải thích:
Hình hộp chữ nhật ABCD. EFGH có 4 đường chéo lần lượt là: FD, EC, HB, GA.
II. Thông hiểu
Câu 1. Cho hình hộp chữ nhật ABCD. EFGH. Chọn khẳng định đúng:
A. AE và BF cắt nhau;
B. ED và HA cắt nhau;
C. EF và GH cắt nhau;
D. AD và BC cắt nhau.
Đáp án: B
Giải thích:
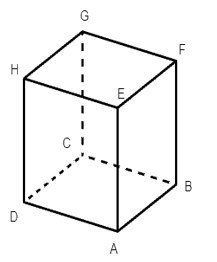
Vì ABCD. EFGH là hình hộp chữ nhật nên ta có:
• AEFB là hình chữ nhật suy ra AE // BF.
Do đó AE và BF không cắt nhau. Vậy A là một khẳng định sai.
• AEHD là hình chữ nhật mà ED và HA là hai đường chéo của hình chữ nhật này nên ED và HA cắt nhau. Vậy B là một khẳng định đúng.
• EFGH là hình chữ nhật suy ra EF // GH.
Do đó EF và GH không cắt nhau. Vậy C là một khẳng định sai.
• ABCD là hình chữ nhật suy ra AD // BC.
Do đó AD và BC không cắt nhau. Vậy D là một khẳng định sai.
Câu 2. Cho hình hộp chữ nhật ABCD. A'B'C'D'. Biết AB = 2 cm. Độ dài cạnh CD và C'D' là
A. CD = C'D' = 1 cm;
B. CD = C'D' = 2 cm;
C. CD = C'D' = 3 cm;
D. CD = C'D' = 4 cm.
Đáp án: B
Giải thích:
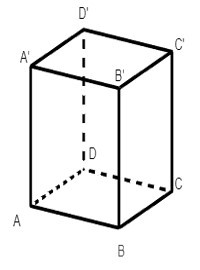
Từ hình hộp chữ nhật ABCD. A'B'C'D' ta có:
AA'B'B là hình chữ nhật suy ra A'B' = AB (1)
A'B'C'D' là hình chữ nhật suy ra C'D' = A'B' (2)
ABCD là hình chữ nhật suy ra CD = AB = 2 cm.
Từ (1) và (2) suy ra C'D' = A'B' = AB = 2 cm.
Vậy CD = C'D' = 2 cm.
Câu 3. Cho hình hộp chữ nhật ABCD. EFGH. Cho AB = 4 cm, BC = 2 cm,
AE = 4 cm. Khẳng định đúng là:
A. HG = 4 cm, HE = 2 cm, GC = 4 cm;
B. HG = 2 cm, HE = 2 cm, GC = 4 cm;
C. HG = 4 cm, HE = 2 cm, GC = 2 cm;
D. HG = 4 cm, HE = 4 cm, GC = 4 cm.
Đáp án: A
Giải thích:
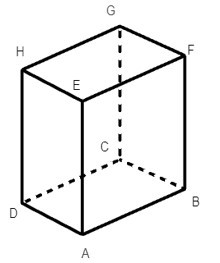
Từ hình hộp chữ nhật ABCD.EFGH ta có các mặt của hình hộp này đều là hình chữ nhật.
Khi đó ta có:
HG = DC = AB = 4 cm;
HE = DA = BC = 2 cm;
GC = HD = AE = 4 cm.
Vậy HG = 4 cm, HE = 2 cm, GC = 4 cm.
Câu 4. Cho hình hộp chữ nhật ABCD.A'B'C'D' có ba kích thước khác nhau. Cạnh có độ dài bằng cạnh AA' là:
A. AB;
B. BC;
C. BB';
D. A'B'.
Đáp án: C
Giải thích:
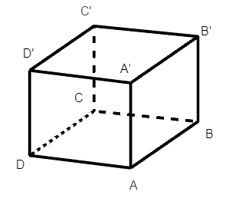
Ta có AA', BB', CC', DD' là các cạnh bên của hình hộp nên ta có:
AA' = BB' = CC' = DD'.
Câu 5. Cho hình hộp chữ nhật ABCD. EFGH. Số đo góc BFG bằng
A. 30°;
B. 60°;
C. 90°;
D. 150°.
Đáp án: C
Giải thích:
Xét hình hộp chữ nhật ABCD. EFGH:
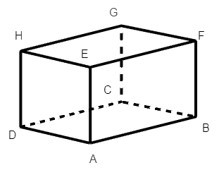
Có ba góc vuông ở đỉnh F là: góc EFG, góc BFE và góc BFG.
Do đó số đo của góc BFG bằng 90°.
Câu 6. Cho hình hộp chữ nhật ABCD. EFGH. Có bao nhiêu cạnh song song với cạnh AE?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
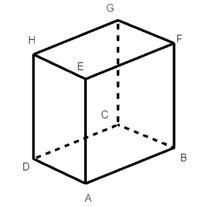
Từ hình hộp chữ nhật ABCD. EFGH ta có:
AEFB là hình chữ nhật suy ra AE // FB.
AEHD là hình chữ nhật suy ra AE // HD.
FBCG là hình chữ nhật suy ra FB // GC.
Mà FB // AE nên GC // AE.
Vậy có ba cạnh song song với AE là FB, HD, GC.
Câu 7. Cho hình hộp chữ nhật EFGH.MNPQ. Khẳng định đúng là:
A. HG = EF = MN = PQ;
B. HE = GF = PN = QM;
C. HQ = GP = FN = EM;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
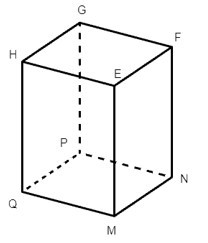
Các nhóm cạnh bằng nhau của hình hộp chữ nhật EFGH. MNPQ là:
HG = EF = MN = PQ; HE = GF = PN = QM; HQ = GP = FN = EM.
Do đó A, B, C đều là những khẳng định đúng.
III. Vận dụng
Câu 1. Cho các miếng bìa sau:
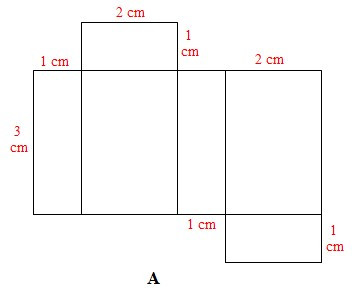
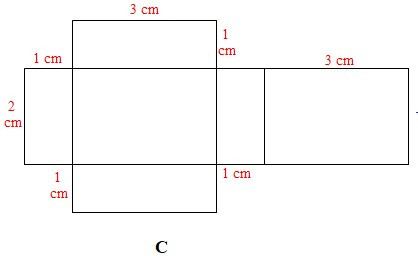
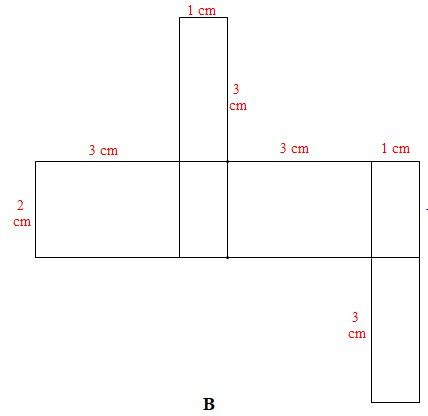
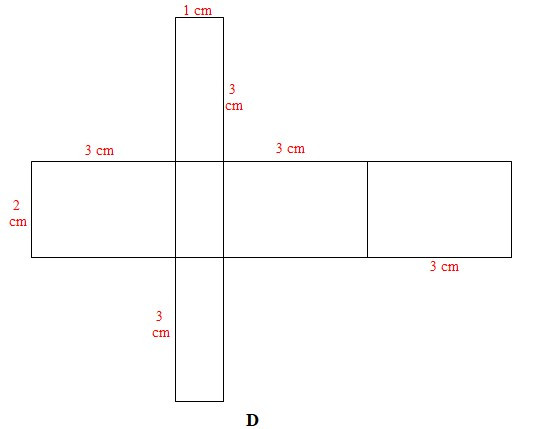
Có mấy tấm bìa gấp được hình hộp chữ nhật có ba kích thước 1 cm, 2 cm, 3 cm?
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án: C
Giải thích:
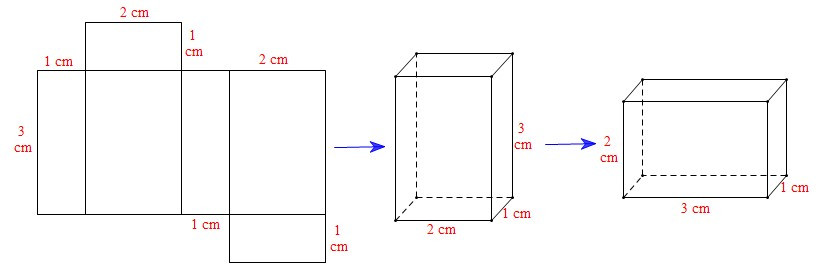
Xét miếng bìa A: Ta gấp được hình hộp chữ nhật sau:
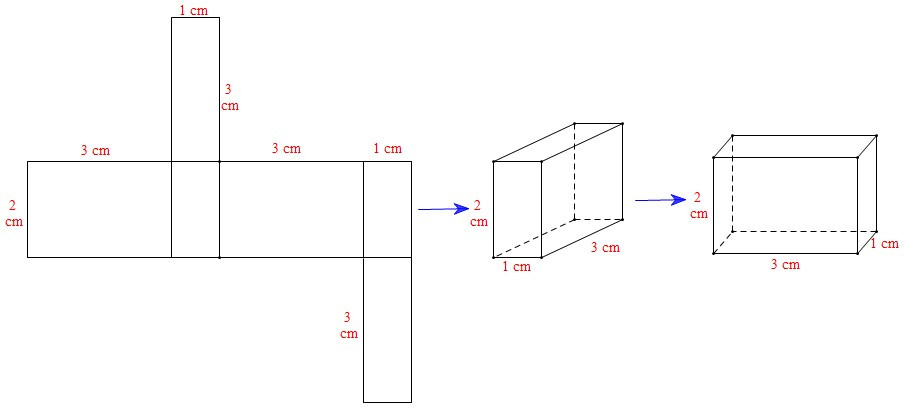
Xét miếng bìa B: Ta gấp được hình hộp chữ nhật sau:
Xét miếng bìa C: Ta gấp được hình hộp chữ nhật sau:
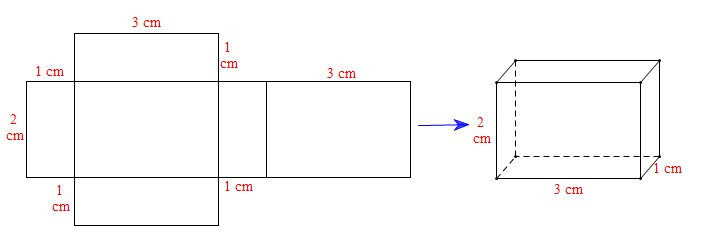
Xét miếng bìa D: Không gấp được hình hộp chữ nhật do chiều dài 3 cm của mặt (1) chưa hợp lí. Để gấp được hình hộp chữ nhật thì kích thước đó của mặt (1) bằng 1 cm.
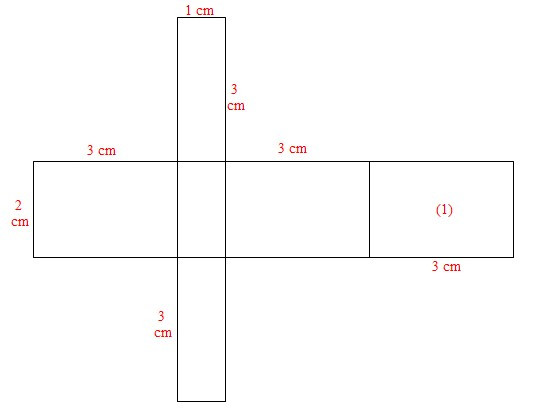
Vậy có 3 tấm bìa gấp được hình hộp chữ nhật có ba kích thước 1 cm, 2 cm, 3 cm.
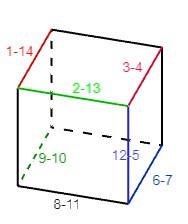
Câu 2. Phải gấp các cạnh nào của hình sau đây với nhau để được một hình lập phương?
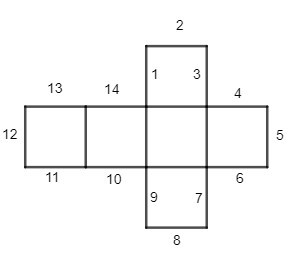
A. 12 và 5, 2 và 13, 1 và 14, 3 và 4, 8 và 11, 9 và 10, 7 và 6;
B. 12 và 5, 2 và 8, 1 và 14, 3 và 4, 13 và 11, 9 và 10, 7 và 6;
C. 12 và 5, 1 và 13, 2 và 14, 3 và 4, 8 và 11, 9 và 10, 7 và 6;
D. 14 và 5, 2 và 13, 1 và 12, 3 và 4, 8 và 11, 9 và 10, 7 và 6.
Đáp án: A
Giải thích:
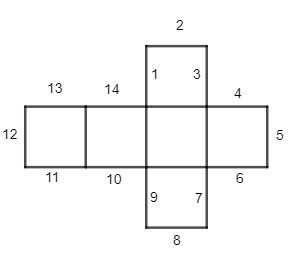
Ta phải gấp các cặp cạnh sau đây với nhau để hình trên trở thành một hình lập phương:
12 và 5, 2 và 13, 1 và 14, 3 và 4, 8 và 11, 9 và 10, 7 và 6.
Khi đó ta được hình vuông sau:
Câu 3. Tấm bìa nào sau đây gấp được hình hộp lập phương?
A. 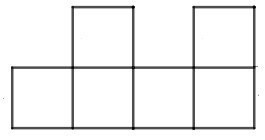
B. 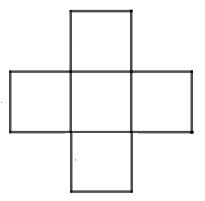
C. 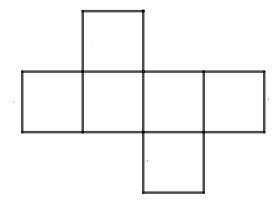
D. 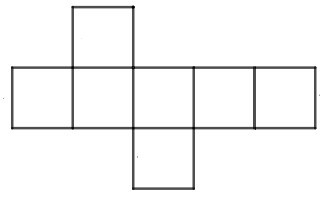
Đáp án: C
Giải thích:
Hình lập phương là hình có 6 mặt.
Quan sát các hình ở từng đáp án ta thấy:
Hình B có tất cả 5 mặt nên không gấp được hình lập phương có 6 mặt. Do đó B sai.
Hình D có tất cả 7 mặt nên không gấp được hình lập phương có 6 mặt. Do đó D sai.
Hình A có hai mặt đáy trên nhưng không có mặt đáy dưới nên A sai.