30 câu Trắc nghiệm Số thực. Giá trị tuyệt đối của một số thực (có đáp án 2024) – Toán 7 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Bài 2: Số thực. Giá trị tuyệt đối của một số thực đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Bài 2.
Trắc nghiệm Toán 7 Bài 2: Số thực. Giá trị tuyệt đối của một số thực
I. Nhận biết
Câu 1. Chọn phát biểu đúng:
A. Số vô tỉ và số hữu tỉ là số thực;
B. Số vô tỉ không phải là số thực;
C. Số thập phân vô hạn tuần hoàn không phải là số thực;
D. Số thập phân vô hạn không tuần hoàn không phải là số thực.
Đáp án: A
Giải thích:
Số vô tỉ và số hữu tỉ là số thực.
Số thập phân vô hạn tuần hoàn là số hữu tỉ. Do đó cũng là số thực.
Số thập phân vô hạn không tuần hoàn là số vô tỉ. Do đó cũng là số thực.
Câu 2. Số đối của số √5 là số:
A. √5
B. -√5
C. 1√5
D. -1√5
Đáp án: B
Giải thích:
Số đối của số √5 là số -√5
Câu 3. Chọn phát biểu đúng:
A. √2∈ℚ;
B. √2∈ℝ;
C. 23∉ℚ;
D. 13∉ℝ.
Đáp án: B
Giải thích:
Ta có:
• 23∈ℚ suy ra C sai.
• 13∈ℝ suy ra D sai.
• √2∉ℚ suy ra A sai.
• √2∈ℝ suy ra B đúng.
Câu 4. Số nào sau đây không phải là số thực:
A. 2;
B. √2;
C. π;
D. Không có đáp án đúng.
Đáp án: D
Giải thích:
Các số 2, √2, π đều là số thực.
Câu 5. |x| =
A. x khi x > 0;
B. –x khi x < 0;
C. 0 khi x = 0;
D. Cả A, B, C đều đúng.
Đáp án: D
Giải thích:
Ta có:
• |x| = x khi x > 0;
• |x| = –x khi x < 0;
• |x| = 0 khi x = 0.
II. Thông hiểu
Câu11. Số đối của các số thực 3; –π; √15 lần lượt là:
A. –3; π; −√15;
B. 3; –π; √15;
C. –3; –π; −√15;
D. 3; π; √15;
Đáp án: A
Giải thích:
Số đối của số 3 là –3;
Số đối của số –π là π;
Số đối của số √15 là số -√15
Vậy số đối của các số thực 3; –π; √15 lần lượt là: –3; π; -√15
Câu 2. Chọn khẳng định đúng.
A. |–0,6| > |–0,7|;
B. |–0,6| = –0,6;
C. |√0,7|>|−√0,7|;
D. |−23|>|13| .
Đáp án: D
Giải thích:
• Ta có –0,6 < 0 nên |–0,6| = –(–0,6) = 0,6. Do đó phương án B sai.
• Vì –0,7 < 0 nên |–0,7| = –(–0,7) = 0,7.
Vì 0,6 < 0,7 nên |–0,6| < |–0,7|. Do đó phương án A sai.
• Vì √0,7 và -√0,7 là hai số đối nhau nên |√0,7|=|−√0,7|.
Do đó phương án C sai.
• Vì −23<0 nên |−23|=−(−23)=23;
Vì 13>0 nên |13|=13;
Vì 23>13 nên |−23|>|13|. Do đó phương án D đúng.
Câu 3. Tính √|−16| ta được kết quả là:
A. – 4;
B. 4;
C. 4 và – 4.
D. Không tồn tại.
Đáp án: B
Giải thích:
Ta có: √|−16|=√16=4
Câu 4. Nhận xét đúng về vị trí của các số thực 0; √3; 52 trên trục số là:
A. Trên trục số, điểm √3 nằm bên trái điểm 52;
B. Trên trục số, điểm √3 nằm bên phải điểm 52;
C. Trên trục số, điểm √3 nằm bên trái điểm 0;
D. Trên trục số, điểm 0 nằm bên phải điểm 52.
Đáp án: A
Giải thích:
Ta có: 0<√3=1,732...<52=2.5
Do đó trên trục số:
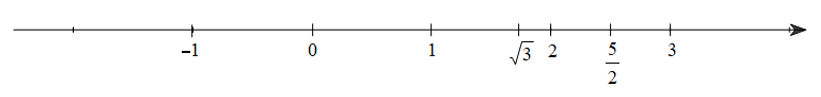
• Điểm √3 nằm bên trái điểm 52. Do đó A đúng và B sai.
• Điểm √3 nằm bên phải điểm 0. Do đó C sai.
• Điểm 0 nằm bên trái điểm 52. Do đó D sai.
Câu 5. Giá trị của biểu thức: |–3,5| + |1,7| – 0,2 là
A. 1,6;
B. –2;
C. 5;
D. –5,4.
Đáp án: C
Giải thích:
Ta có: |–3,5| + |1,7| – 0,2
= 3,5 + 1,7 – 0,2
= 5
Câu 6. Có bao nhiêu số thực x thỏa mãn |x| = 2?
A. 3;
B. 2;
C. 1;
D. 0.
Đáp án: B
Giải thích:
Ta có |x| = 2
Suy ra x = 2 hoặc x = –2.
Vậy có hai số thực x thỏa mãn |x| = 2 là 2 và –2.
Câu 7. Có bao nhiêu số thực x thỏa mãn |x|=−√3?
A. 3;
B. 2;
C. 1;
D. 0.
Đáp án: D
Giải thích:
Do |x| luôn không âm mà −√3<0 nên không có số thực x nào thỏa mãn điều kiện đề bài.
III. Vận dụng
Câu 1. Cho một hình vuông có diện tích 12 m2. Hãy so sánh độ dài cạnh a của hình vuông đó và độ dài b = 3,47 m.
A. a = b;
B. a > b;
C. a < b;
D. Không thể so sánh được.
Đáp án: C
Giải thích:
Độ dài cạnh của hình vuông đó là:
a=√12=3,4641016....<3,47
Vậy a < b.
Câu22. Giá trị của biểu thức A=√(√3−1)2−√(1−√3)2
A. 2√3−2;
B. 0;
C. √3−1;
D. 2−2√3.
Đáp án: B
Giải thích:
Ta có:
A=√(√3−1)2−√(1−√3)2
=|√3−1|−|1−√3|
Ta có: √3=1,732050808 > 1
Nên √3−1>0 và 1−√3<0
Do đó: |√3−1|=√3−1 và |1−√3|=√3−1.
Khi đó A=(√3−1)−(√3−1)=0
Câu33. Có bao nhiêu giá trị x thoả mãn 7,5 – 3.|5 – 2x| = –4,5?
A. 0;
B. 1;
C. 2;
D. 3.
Đáp án: C
Giải thích:
Ta có:
7,5 – 3.|5 – 2x| = –4,5
3.|5 – 2x| = 7,5 –(–4,5)
3.|5 – 2x| = 7,5 + 4,5
3.|5 – 2x| = 12
|5 – 2x| = 12 : 3
|5 – 2x| = 4
Trường hợp 1: 5 – 2x = 4
2x = 5 – 4
2x = 1
x=12
Trường hợp 2: 5 – 2x = –4
2x = 5 – (–4)
2x = 5 + 4
2x = 9
x = 9 : 2
x=92
Vậy có hai giá trị của x thoả mãn là x=12; x=92.