30 câu Trắc nghiệm Ôn tập chương 1 (có đáp án 2024) – Toán 7 Chân trời sáng tạo
Bộ 30 câu hỏi trắc nghiệm Toán 7 (có đáp án) Ôn tập chương 1 đầy đủ các mức độ sách Chân trời sáng tạo giúp học sinh ôn luyện trắc nghiệm Toán 7 Chương I.
Trắc nghiệm Toán 7 Chương 1: Số hữu tỉ
I. Nhận biết
Câu 1. Số hữu tỉ là số được viết dưới dạng:
A. ab;
B. ab, với a, b ∈ ℤ;
C. ab, với b ≠ 0;
D. ab, với a, b ∈ ℤ; b ≠ 0.
Đáp án: D
Giải thích:
Số hữu tỉ là số được viết dưới dạng phân số ab, với a, b ∈ ℤ; b ≠ 0.
Câu 2. Chọn khẳng định đúng:
A. x – (y + z – t) = x + y + z – t;
B. x – (y + z – t) = x – y – z + t;
C. x – (y + z – t) = x + y + z + t;
D. x – (y + z – t) = x + y – z – t.
Đáp án: B
Giải thích:
Khi bỏ dấu ngoặc, trước dấu ngoặc có dấu “–“ thì đổi dấu tất cả các số hạng trong ngoặc nên x – (y + z – t) = x – y – z + t;
Câu 3. Với x, y ∈ ℚ, m, n ∈ ℕ*, m > n, khi đó:
A. (x : y)m = xm : ym;
B. xm – xn = xm - n;
C. x0 = 1;
D. (xm)n = xm. n.
Đáp án: D
Giải thích:
Ta có:
(x:y)m = xm : ym với y ≠ 0 nên A sai.
xm : xn = xm – n nên B sai.
x0 = 1 với x ≠ 0 nên C sai.
(xm)n = xm. n nên D đúng.
Câu 4. Chọn khẳng định sai.
A. Số đối của 32 là -32;
B. Số đối của 32 là -3-2;
C. Số đối của số 0 là 0;
D. Số đối của 32 là −112.
Đáp án: B
Giải thích:
Số đối của 32 là −32=−112 nên A, D đúng.
Số đối của số 0 là số 0 nên C đúng.
Ta có −3−2=32 nên −3−2 không là số đối của 32 nên B sai.
Câu 5. Số 312 không là kết quả của số nào trong các số sau đây?
A. 318 : 36;
B. 34. 38;
C. 32. 36;
D. (33)4.
Đáp án: C
Giải thích:
Ta có: 318 : 36 = 318 – 6 = 312;
34. 38 = 34 + 8 = 312;
32. 36 = 32 + 6 = 38 ≠ 312;
(33)4 = 33. 4 = 312.
Câu 6. Trong các điểm M, N, P được biểu diễn trên trục số thì điểm nào biểu diễn số hữu tỉ âm?

A. Điểm M;
B. Điểm N;
C. Điểm P;
D. Điểm O.
Đáp án: B
Giải thích:
Điểm N nằm trước gốc O nên biểu diễn số hữu tỉ âm.
Câu 7. Điền dấu thích hợp vào ô trống: 2110.0,3+0,7.2110 2110(0,3+0,7)
A. >;
B; <;
C. =;
D. ≠.
Đáp án: C
Giải thích:
Ta có: 2110.0,3+0,7.2110=2110(0,3+0,7)
Câu 8. Cho biểu thức 21+154:(38−16).57. Chọn khẳng định đúng?
A. Ta cần thực hiện phép tính trừ trước;
B. Ta cần thực hiện phép chia trước;
C. Ta cần thực hiện phép nhân trước;
D. Ta cần thực hiện phép cộng trước.
Đáp án: A
Giải thích:
Với các biểu thức có dấu ngoặc, ta thực hiện trong ngoặc trước, ngoài ngoặc sau.
Vì các phép tính cộng, nhân, chia ở ngoài ngoặc và phép tính trừ ở trong ngoặc, nên ta thực hiện phép tính trừ trước.
Câu 9. Khi thực hiện phép tính có dấu ngoặc, thứ tự thực hiện nào sau đây đúng?
A. [ ] → ( ) → { };
B. ( ) → [ ] →{ };
C. { } → [ ] →( );
D. [ ] →{ } →( ).
Đáp án: B
Giải thích:
Khi thực hiện tính toán biểu thức có dấu ngoặc, ta thực hiện theo thứ tự: ngoặc tròn, ngoặc vuông, ngoặc nhọn.
Câu 10. Chọn khẳng định đúng?
A. Mọi số nguyên đều là số tự nhiên;
B. Mọi số hữu tỉ đều là số tự nhiên;
C. Mọi số tự nhiên đều là số hữu tỉ;
D. Mọi số thập phân đều là số nguyên.
Đáp án: C
Giải thích:
Ta đưa ra các ví dụ như sau:
Số –2 là số nguyên nhưng không phải số tự nhiên nên A sai.
Số –1,2 là số hữu tỉ nhưng không phải số tự nhiên nên B sai.
Mọi số tự nhiên a đều được viết dưới dạng a1 với a ∈ ℤ nên C đúng.
Số 1,3 là số thập phân nhưng không phải số nguyên nên D sai.
II. Thông hiểu
Câu 1. Cho các điểm A, B, C, D lần lượt biểu diễn các số −212;0;−32;12 trên trục số. Các điểm biểu diễn các số theo thứ tự từ trái sang phải theo chiều dương trên trục số là:
A. A, B, C, D;
B. A, C, B, D;
C. D, B, C, A;
D. B, C, A, D.
Đáp án: B
Giải thích:
+) Biểu diễn số −212:
Ta có: −212=−52
Ta chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 tới điểm 1) thành 2 phần bằng nhau, ta được đoạn đơn vị mới bằng 12 đơn vị cũ.
Số hữu tỉ −52 được biểu diễn bởi điểm A nằm về phía bên trái gốc O và cách O một đoạn bằng 5 đơn vị mới (Hình vẽ)
Tương tự, ta có các điểm B, C, D biểu diễn các số 0;−32;12 trên trục số như hình vẽ dưới đây:
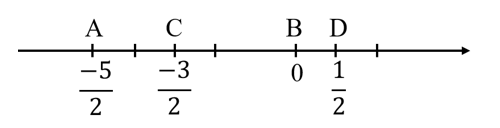
Quan sát trên trục số ta thấy thứ tự từ trái sang phải trên trục số là: A, C, B, D.
Câu 2. Tìm số tự nhiên n biết: 162n=2
A. n = 3;
B. n = 4;
C. n = 2;
D. n = 1.
Đáp án: A
Giải thích:
Ta có: 162n=2
Suy ra 242n=2
Hay 24 – n = 21
Khi đó 4 – n = 1
Vậy n = 3.
Câu 3. Tìm x, biết: (x + 3)3 = −125
A. x = –8;
B. x = 0;
C. x = −16;
D. x = 12.
Đáp án: A
Giải thích:
Ta có (x + 3)3 = −125
Hay (x + 3)3 = (–5)3
Khi đó x + 3 = –5
Do đó x = –5 – 3
Vậy x = –8
Câu 4. Tính diện tích hình thang có các kích thước như hình:
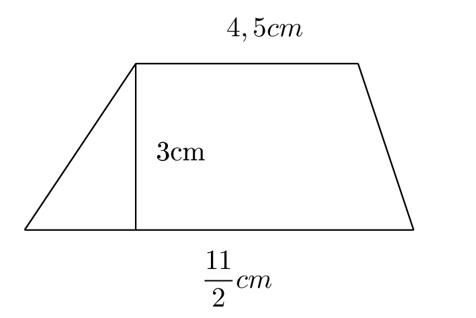
A. 15 cm2;
B. 30 cm2;
C. 15 cm;
D. 30 cm.
Đáp án: A
Giải thích:
Diện tích hình thang là:
(4,5+112).3: 2
=(92+112).3:2
= 10. 3: 2
= 15 (cm2)
Câu 5. Sắp xếp các số hữu tỉ sau theo thứ tự tứ nhỏ đến lớn: –2; 0; −35; 45.
A. −35; 0; –2; 45;
B. −35; –2; 0; 45;
C. –2; −35; 0; 45;
D. –2; −35; 45; 0.
Đáp án: C
Giải thích:
• Ta có: −2=−105 và −35=−35.
Vì –10 < –3 nên −105<−35
Do đó –2 < −35
• Mà số 0 luôn lớn hơn số hữu tỉ âm và luôn nhỏ hơn số hữu tỉ dương.
Trong các số –2; 0; −35; 45 thì có các số hữu tỉ âm là –2; −35 và số hữu tỉ dương là 45
Do đó −2<−35<0<45.
Vậy các số được sắp xếp theo thứ tự từ nhỏ đến lớn là –2; −35; 0; 45.
Câu 6. Thực hiện phép tính: 27+27:(−23)+12 ta được kết quả là:
A. 314;
B. 414;
C. 514;
D. 614.
Đáp án: C
Giải thích:
27+27:(−23)+12=27+27.(−32)+12
=27−37+12=−17+12=−214+714=514
Câu 7. Tìm số x, biết (13)2x−1=1243.
A. x = 13;
B. x = 10;
C.x = 8;
D. x = 3.
Đáp án: D
Giải thích:
Ta có (13)2x−1=1243.
(13)2x−1=135.
(13)2x−1=(13)5.
Suy ra 2x – 1 = 5.
2x = 5 + 1.
2x = 6.
x = 6 : 2.
x = 3.
Câu 8. Thực hiện phép tính: 54.204255.45
A. 110;
B. 1100;
C. 5100;
D. 125.
Đáp án: B
Giải thích:
54.204255.45=(5.20)4(25.4)5=10041005=1100
Câu 9. Nhiệt độ T (℃) của môi trường không khí và độ cao h (mét) ở một địa phương được tính bởi công thức: T = 28 – 3500. h (℃). Nhiệt độ tại một đỉnh núi có độ cao khoảng 1543 m là:
A. 18,4 ℃;
B. 18,7 ℃;
C. 19 ℃;
D. 19,8 ℃.
Đáp án: B
Giải thích:
Ta có: T = 28 – 3500. 1543 = 18,7
Vậy nhiệt độ trên đỉnh núi có độ cao 1543 m là 18,7℃.
Câu 10. Số 23 được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
A.

B.
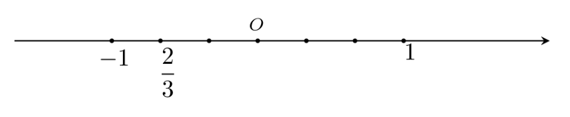
C.
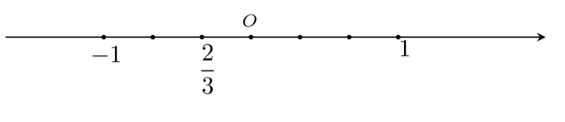
D.
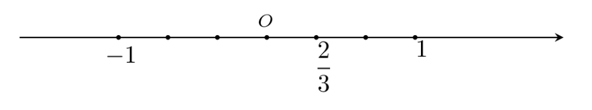
Đáp án: A
Giải thích:
Biểu diễn số 23 trên trục số ta làm như sau:
+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 3 phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng 23 đơn vị cũ.
+ Số 23 được biểu diễn bởi điểm nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới.

Câu 11. Giá trị của biểu thức H=3.[56−15:(110+14)] bằng:
A. 1411;
B. 914;
C. 1114;
D. 1514.
Đáp án: C
Giải thích:
Ta có H=3.[56−15:(110+14)]
=3.[56−15:(220+520)]
=3.(56−15:720)
=3.(56−15.207)
=3.(56−47)
=3.(3542−2442)
=3.1142=1114.
Câu 12. Giá trị của (−25).43+(−310).43 bằng:
A. −114;
B. −1415;
C. −215;
D. −818.
Đáp án: B
Giải thích:
Ta có (−25).43+(−310).43
=[−25+(−310)].43
=(−410+−310).43
=−710.43
=−75.23
=−1415
Câu 13. Giá trị của (−23):53+(−34):53 bằng:
A. −1720;
B. −120;
C. −112;
D. −115.
Đáp án: A
Giải thích:
Ta có (−23):53+(−34):53
=(−23).35+(−34).35
=[−23+(−34)].35
=(−812+−912).35
=−1712.35
=(−17).33.4.5
=−1720
Câu 14. Khối lượng của Trái Đất khoảng 5,97.1024 kg, khối lượng của Mặt Trăng khoảng 7,35.1022 kg. Khối lượng của Trái Đất lớn hay Mặt Trăng lớn hơn và lớn hơn bao nhiêu?
A. Mặt Trăng nặng hơn Trái Đất 5,8965.1024 kg;
B. Trái Đất nặng hơn Mặt Trăng 5,8965.1024 kg;
C. Mặt Trăng nặng hơn Trái Đất 5,8965.1022 kg;
D. Trái Đất nặng hơn Mặt Trăng 5,8965.1022 kg.
Đáp án: B
Giải thích:
Ta có: 7,35.1022 = 0,0735.1024
Vì 5,97 > 0,0735 nên 5,97.1024 > 0,0735.1024
Do đó Trái Đất nặng hơn Mặt Trăng, và nặng hơn là:
5,97.1024 – 0,0735.1024
= (5,97 – 0,0735).1024 = 5,8965.1024 (kg).
Vậy Trái Đất nặng hơn Mặt Trăng 5,8965.1024 kg.
III. Vận dụng
Câu 1. Số hữu tỉ x=aa2+1 (với a là số nguyên) nhận giá trị âm khi:
A. a = –1;
B. a = 0;
C. a = 1;
D. a ∈ ℤ.
Đáp án: A
Giải thích:
Ta có a2 ≥ 0, với mọi a ∈ ℤ.
Suy ra a2 + 1 ≥ 1 > 0, với mọi a ∈ ℤ.
Để x nhận giá trị âm thì x < 0, nghĩa là aa2+1<0.
Khi đó a và a2 + 1 trái dấu
Mà a2 + 1 > 0 (chứng minh trên).
Suy ra a < 0 và a là số nguyên (*)
Xét phương án A: a = –1 thoả mãn điều kiện (*).
Xét phương án B: a = 0 không thoả mãn điều kiện (*).
Xét phương án C: a = 1 không thoả mãn điều kiện (*).
Xét phương án D: a ∈ ℤ không thoả mãn điều kiện (*).
Vậy a = –1 thoả mãn yêu cầu đề bài.
Câu 2. Bác Minh gửi tiết kiệm 120 triệu đồng vào một ngân hàng với kì hạn 1 năm. Hết kì hạn, bác Minh nhận được cả gốc và lãi là 127,2 triệu đồng. Lãi suất ngân hàng là:
A. 4%;
B. 5%;
C. 6%;
D. 7%.
Đáp án: C
Giải thích:
Số tiền lãi mà bác Minh nhận được sau một năm là:
127,2 – 120 = 7,2 triệu đồng
Lãi suất ngân hàng là:
7,2 : 120. 100% = 6%
Câu 3. Bác An mua ba món hàng ở một siêu thị: Món hàng thứ nhất giá niêm yết 140 000 đồng và được giảm giá 30%; món hàng thứ hai giá niêm yết 480 000 đồng và được giảm giá 20%; món hàng thứ ba được giảm 40%. Tổng số tiền bác An phải thanh toán là 950 000 đồng. Giá niêm yết của món hàng thứ là:
A. 760 000 đồng;
B. 780 000 đồng;
C. 800 000 đồng;
D. 820 000 đồng.
Đáp án: B
Giải thích:
Vì món hàng thứ nhất bác An được giảm 30% nên số tiền mà bác An cần trả bằng 70% giá tiền niêm yết.
Giá tiền bác An trả cho món hàng ban đầu là:
140 000.70% = 140 000.70100 = 98 000 (đồng).
Vì món hàng thứ hai bác An được giảm 20% nên số tiền bác An cần trả bằng 80% giá tiền niêm yết.
Giá tiền bác An trả cho món hàng thứ hai là:
480 000. 80% = 480 000. 80100 = 384 000 (đồng)
Số tiền bác An trả cho món hàng thứ ba là:
950 000 – 98 000 – 384 000 = 468 000 (đồng)
Vì mặt hàng thứ ba, bác An được giảm 40% nên số tiền bác An cần trả bằng 60% giá tiền niêm yết.
Giá niêm yết của món hàng thứ ba là:
468 000 : 60% = 780 000 (đồng)
Câu 4. Cho B=21.3. Khẳng định nào sau đây là đúng?
A. B < 1;
B. B = 1;
C. B > 1;
D. B ∈ ℤ.
Đáp án: A
Giải thích:
Ta có
.
Vậy . Do đó B và D sai.
Ta có 100 < 101 nên
Hay B < 1. Do đó A là đúng.
Câu 5. Cho số hữu tỉ . Giá trị x nguyên dương thoả mãn số hữu tỉ y nguyên là:
A. x ∈ ∅;
B. x ∈ {–3; –1; 0; 2; 3; 5};
C. x ∈ {–3};
D. x ∈ {2; 3; 5}.
Đáp án: D
Giải thích:
Để là số hữu tỉ thì x – 1 ≠ 0 hay x ≠ 1
Ta có .
Số hữu tỉ y nhận giá trị nguyên (với x nguyên) khi và chỉ khi 4 ⋮ (x – 1) hay x – 1 là ước của 4
Mà Ư(4) = {–4; –2; –1; 1; 2; 4}.
Ta có bảng sau:
|
x – 1 |
–4 |
–2 |
–1 |
1 |
2 |
4 |
|
x |
–3 |
–1 |
0 |
2 |
3 |
5 |
Mà x cần tìm có giá trị nguyên dương và x ≠ 1 nên x ∈ {2; 3; 5}
Vậy x ∈ {2; 3; 5} thì y nhận giá trị nguyên.